无源低通滤的电路曲线及方程案例频率摘要

低通滤波器是一种可用于修改，重塑或拒绝所有不需要的高频电信号并接受或仅通过电路设计者所需信号的电路

换句话说，它们“滤除”不需要的信号，理想滤波器将基于其频率分离并传递正弦输入信号。在低频应用（高达100kHz）中，无源滤波器通常使用简单的 RC （电阻 - 电容）网络构建，而高频滤波器（100kHz以上）通常由 RLC构成（电阻 - 电感 - 电容）元件。

无源滤波器由无源元件组成，如电阻，电容和电感，没有放大元件（晶体管，运算放大器等），所以没有信号增益，因此它们的输出电平始终小于输入。

滤波器根据它们允许通过的信号的频率范围命名，同时阻塞或“衰减”其余信号。最常用的滤波器设计是：

低通滤波器 - 低通滤波器仅允许从0Hz到其截止频率的低频信号频率，ƒc指向阻塞那些更高的频率。

高通滤波器 - 高通滤波器只允许高频信号从其截止频率，ƒc点和更高频率到无效通过，同时阻挡那些更低的。

带通滤波器 - 带通滤波器允许落在两点之间的某个频带设置内的信号通过，同时阻止两者该频带两侧的频率越来越低。

简单的一阶无源滤波器（一阶）可以通过在输入端串联一个电阻和一个电容串来实现信号，（V IN ），滤波器的输出，（V OUT ）取自这两个分量的连接点。

De关于输出信号连接电阻器和电容器的方式决定了滤波器结构的类型，导致低通滤波器或高通滤波器。

由于任何滤波器的功能是允许给定频带的信号不变地通过，同时衰减或削弱所有其他不需要的频率，我们可以通过以下方式定义理想滤波器的幅度响应特性：使用如图所示的四种基本滤波器类型的理想频率响应曲线。

理想滤波器响应曲线

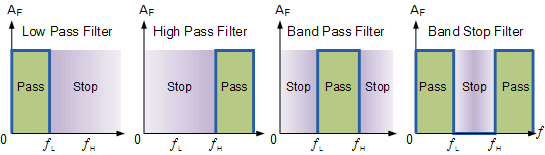
过滤器可分为两种不同的类型：有源滤波器和无源滤波器。有源滤波器包含放大装置以增加信号强度，而无源滤波器不包含放大装置以增强信号。由于无源滤波器设计中有两个无源元件，输出信号的幅度小于相应的输入信号，因此无源 RC 滤波器衰减信号并且增益小于1，（单位） 。

低通滤波器可以是电容，电感或电阻的组合，旨在产生高于指定频率的高衰减，并且在该频率以下很少或没有衰减。发生转换的频率称为“截止”或“拐角”频率。

最简单的低通滤波器由电阻和电容组成，但更复杂的低通滤波器具有串联组合电感器和并联电容器。在本教程中，我们将介绍最简单的类型，无源双组件RC低通滤波器。

低通滤波器

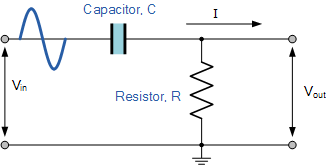
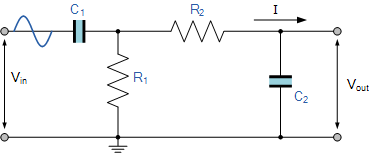
简单的无源RC低通滤波器或LPF，可通过将单个电阻串联连接在一起而轻松制作，如下图所示。在这种类型的滤波器布置中，输入信号（V IN ）应用于串联组合（电阻器和电容器一起），但输出信号（V OUT ）是仅通过电容器。

这种类型的滤波器通常称为“一阶滤波器”或“单极滤波器”，为什么是一阶或单极？，因为它只有电路中的“一”电抗元件，电容器。

RC低通滤波器电路

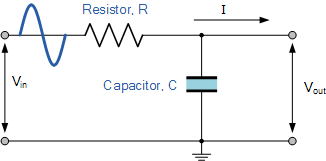
如前面电容电抗教程中所述，电容的电抗与频率成反比，而电阻值随频率的变化保持不变。在低频时，与电阻器的电阻值 R 相比，电容器的容抗（X C ）将非常大。

这意味着电容两端的电压电位V C 将远大于电阻上产生的电压降V R 。在高频时，反之亦然，V C 小，V R 由于容抗电容值的变化而变大。

上面的电路是RC低通滤波器电路，它也可以被认为是一个频率相关的可变分压器电路，类似于我们在电阻器教程中看到的那样。在该教程中，我们使用以下公式计算串联连接的两个单电阻的输出电压。

我们也知道交流电路中电容器的容抗电阻如下：

反对电流交流电路中的流量称为阻抗，符号 Z ，对于由单个电阻与单个电容串联组成的串联电路，电路阻抗计算如下： / p>

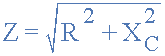
然后通过将我们的等式代入上面的阻抗进入电阻分压器方程给出：

RC分压器方程

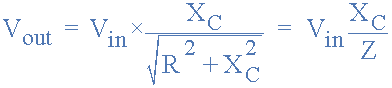
因此，通过使用串联的两个电阻器的分压器方程式来代替对于阻抗，我们可以计算任何给定频率的 RC滤波器的输出电压。

低通滤波器示例No1

A低通滤波器电路由ar组成与 47nF 电容串联的4k7Ω的电阻连接在 10v 正弦电源上。以100Hz的频率计算输出电压（ V OUT ），再次以10,000Hz或10kHz的频率计算。

电压输出频率为的100Hz。

频率为10,000Hz（10kHz）的电压输出。

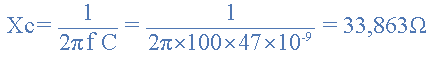
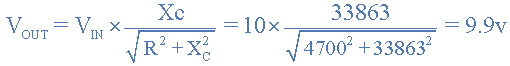
频率响应

从上面的结果可以看出，随着施加到RC网络的频率从100Hz增加到10kHz，电压电容下降，因此电路的输出电压（ V OUT ）从9.9v降至0.718v。

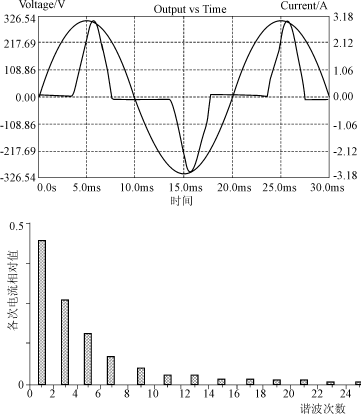
通过将网络输出电压绘制成不同的输入频率值，可以找到低通滤波器电路的频率响应曲线或Bode Plot功能，如图所示

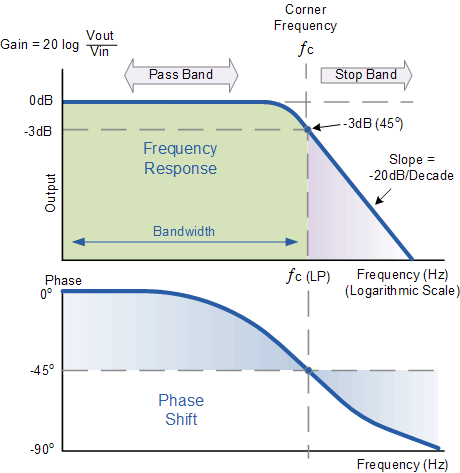
一阶低通滤波器的频率响应

Bode情节显示滤波器的频率响应对于低频几乎是平坦的，并且所有输入信号都直接传递到输出，导致增益接近 1 ，称为“统一”，直到达到截止频率点（ƒc）。这是因为电容器的电抗在低频时很高，并阻止任何电流流过电容器。

在此截止频率点之后，电路的响应在斜率为 -20dB /十度或（-6dB / Octave）“滚降”。请注意，对于任何RC组合，斜率的角度，此 -20dB / Decade 滚降将始终相同。

应用于低通滤波器的任何高频信号超过此截止频率点的电路将大大衰减，即它们迅速减小。发生这种情况是因为在非常高的频率下，电容器的电抗变得很低，导致输出端子短路，导致零输出。

然后仔细选择正确的电阻器 - 电容器组合，我们可以创建一个RC电路，允许低于某个值的频率范围通过电路不受影响，同时应用于该截止点上方的电路的任何频率都会衰减，从而产生通常称为a低通滤波器。

对于这种类型的“低通滤波器”电路，低于此截止频率的所有频率，ƒc点几乎没有变化没有衰减，据说是在滤波器通带区。此通带区域还表示滤波器的带宽。高于此点截止点的任何信号频率通常都被认为是在滤波器阻带区域内，并且它们将大大衰减。

这个“截止”，“拐角“或”断点“频率定义为容抗和电阻相等的频率点， R = Xc =4k7Ω。当发生这种情况时，输出信号衰减到输入信号值的 70.7％或输入的-3dB（20 log（Vout / Vin））。虽然 R = Xc ，但输出不是输入信号的一半。这是因为它等于两者的矢量和，因此是输入的0.707。

由于滤波器包含电容，因此相角（Φ）输出信号LAGS在输入信号后面，-3dB截止频率（ƒc）与-45 o 相位不同。这是由于在输入电压变化时对电容器极板充电所花费的时间，导致输出电压（电容器两端的电压）滞后于输入信号的电压。施加到滤波器的输入频率越高，电容器滞后越多，电路越来越“异相”。

截止频率点和相移角可以通过使用下列等式：

截止频率和相移

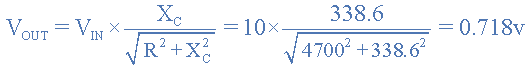
然后为我们的简单上面的“低通滤波器”电路示例中，截止频率（ƒc）为 720Hz ，输出电压为70.7输入电压值的百分比和相移角 -45 o 。

二阶低通滤波器

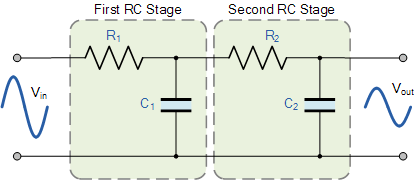
到目前为止，我们已经看到，通过将单个电阻器与单个电容器串联连接，可以制造简单的一阶RC低通滤波器。这种单极布置为我们提供了在 f -3dB 的截止点以上-20dB / decade频率衰减的滚降斜率。但是，有时在滤波器电路中，这个-20dB /十倍（-6dB /倍频程）的斜率角可能不足以去除不需要的信号，然后可以使用两级滤波，如图所示。

命令低通滤波器

上述电路使用两个无源一阶低通滤波器连接或“级联”一起形成二阶或二极滤波器网络。因此，我们可以看到一阶低通滤波器可以通过简单地向其添加一个额外的 RC 网络转换为二阶类型，并且我们添加的更多RC阶段变为更高的阶段过滤器。

如果这些RC级的数字（ n ）级联在一起，则产生的RC滤波器电路将被称为“n th -order” 滤波器的滚降斜率为“nx -20dB / decade”。

因此，例如，二阶滤波器的斜率为-40dB / decade（-12dB / octave） ），四阶滤波器的斜率为-80dB / decade（-24dB / octave），依此类推。这意味着，随着滤波器阶数的增加，滚降斜率变得更陡峭，滤波器的实际阻带响应接近其理想的阻带特性。

二阶滤波器很重要，因为与一阶滤波器结合使用时，可以使用它们设计任何高阶n th 值滤波器。例如，通过串联或级联一阶和二阶低通滤波器来形成三阶低通滤波器。

但是，RC滤波器阶段也存在一个下行趋势。尽管可以形成滤波器的顺序没有限制，但随着阶数的增加，最终滤波器的增益和精度会下降。

当相同的RC滤波器级级联在一起时，输出增益在所需的截止频率（ƒc）减少（衰减）相对于用作滚降斜率增加的滤波器级数的量。我们可以使用以下公式定义所选截止频率的衰减量。

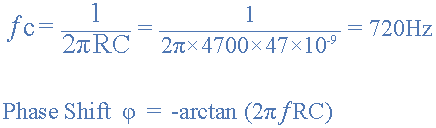
其中“ n ”是滤波器级数。

因此对于二阶无源低通滤波器，转角频率的增益ƒc 将等于0.7071 x 0.7071 = 0.5Vin（-6dB），三阶无源低通滤波器将等于0.353Vin（-9dB），四阶将为0.25Vin（-12dB）并且等等。二阶无源低通滤波器的转折频率ƒc由电阻/电容（RC）组合决定，并给出为。

二阶滤波器转角频率

实际上随着滤波器阶段及其滚降斜率增加，低通滤波器-3dB转角频率点，因此其通带频率从上面的原始计算值变化一个由下式确定的量。

二阶低通滤波器-3dB频率

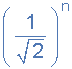
其中ƒc是计算的截止频率， n 是滤波器顺序， ƒ -3dB 是新的-3dB通带频率，这是滤波器阶数增加的结果。

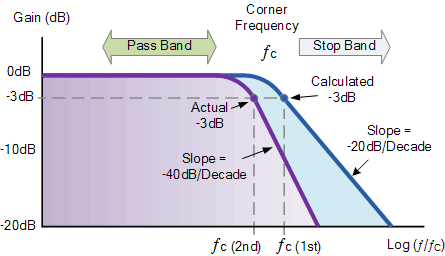
然后是频率响应（波特图） ）对于二阶低通滤波器，假设相同的-3dB截止点看起来像：

二阶低通滤波器的频率响应

实际上，由于每个滤波器阶数的动态阻抗会影响其相邻网络，因此难以精确地实现级联无源滤波器以生成更大阶滤波器。但是，为了降低负载效应，我们可以使每个后续级10x的阻抗位于前一级，因此 R2 = 10 x R1 和 C2 = 1/10 C1 。二阶及以上滤波器网络通常用于运算放大器的反馈电路中，通常称为有源滤波器或RC振荡器电路中的相移网络。

低通滤波器摘要

总而言之，低通滤波器具有恒定的输出电压，从DC（0Hz）到指定的截止频率，（ƒ C ）点。该截止频率点是允许通过的电压增益的0.707或-3dB（dB = -20log * V OUT / IN ）。

此截止点“span”ƒ C 的“低于”频率范围通常称为通带，因为允许输入信号通过过滤器。 “截止点”以上的频率范围通常称为阻带，因为输入信号被阻止或停止通过。

简单的一阶低通滤波器可以使用单个电阻与输入信号 Vin 上的单个非极化电容（或任何单个电抗元件）串联，而输出信号 Vout 是取自电容器。

截止频率或-3dB点，可使用标准公式ƒc= 1 /（2πRC）找到。对于低通滤波器，ƒc处的输出信号的相位角为 -45 o 。

增益过滤器或任何过滤器，通常用分贝表示，它是输出值除以相应输入值的函数，给出如下：

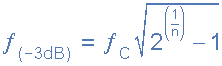
无源低通滤波器的应用在音频放大器和扬声器系统中，用于将低频低音信号导向较大的低音扬声器或降低任何高音频率噪声或“嘶嘶”型失真。在音频应用中使用时，低通滤波器有时被称为“高切”或“高音切割”滤波器。

如果我们要反转电路中电阻和电容的位置为了使输出电压从电阻两端获得，我们将得到一个产生类似于高通滤波器的输出频率响应曲线的电路，这将在下一个教程中讨论。

时间常数

到目前为止，我们一直对低压滤波器受到正弦波形时的频率响应感兴趣。我们还看到滤波器截止频率（ƒc）是电路中电阻（R）和电容（C）相对于某个指定频率点的乘积，并且通过改变两个分量中的任何一个来改变这个截止频率点可以通过增大或减小来实现。

我们也知道电路的相移落后于输入信号的相移，因为充电然后对电容放电所需的时间随着正弦波的变化。这种 R 和 C 的组合会对电容器产生充电和放电效应，称为电路的时间常数（τ），如下所示。 RC电路教程为滤波器提供了时域响应。

时间常数tau（τ）与截止频率ƒc相关：

或以截止频率表示，ƒc为：

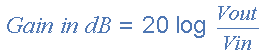
输出电压V OUT 取决于时间常数和输入信号的频率。随着时间平滑变化的正弦信号，电路就像我们上面看到的一样简单的一阶低通滤波器。

但是如果我们要将输入信号改为“正方形”波形“成形”ON / OFF“类型信号，具有几乎垂直的阶跃输入，现在我们的滤波器电路会发生什么。电路的输出响应会发生显着变化，并产生另一种通常称为积分器的电路。

RC积分器

积分器基本上是在时域中工作的低通滤波器电路，当电容器充电和放电时，它将方波“阶跃”响应输入信号转换成三角形波形输出。三角波形由交替但相等的正负斜坡组成。

如下所示，如果 RC 时间常数与输入波形的时间长度相比较长，则输出波形将呈三角形，输入频率越高，输出频率越低。输出幅度与输入的幅度相比。

RC积分电路

这使得此类电路成为理想选择用于将一种类型的电子信号转换为另一种用于波浪发生或波形整形电路的电子信号。