电感器是一种无源电气元件,由线圈组成,设计用于利用电流通过线圈的方式与电力和电力之间的关系.
在我们关于电磁学的教程中,我们看到当电流流过导线时,在导体周围产生磁通量。这种影响产生了围绕导体循环的磁通方向与流过同一导体的电流方向之间的关系。这导致了电流和磁通量方向之间的关系,称为“弗莱明的右手规则”。
但是还存在与缠绕线圈相关的另一个重要特性,即二次电压是通过磁通量的移动引入相同的线圈,因为它反对或抵抗流过它的电流的任何变化。
典型的电感
在最基本的形式中,电感器只不过是缠绕在中心核心周围的线圈。对于大多数线圈而言,流过线圈的电流( i )会在其周围产生一个磁通量(NΦ),与该电流流量成正比。
电感器,也称为扼流圈,是另一种无源型电气元件,由一个线圈组成,设计用于通过在其自身或其核心内感应磁场来利用这种关系。电流流过线圈的结果。将线圈形成电感器会产生比由简单线圈产生的线圈强得多的磁场。
电感器由紧密缠绕在实心中心核心周围的导线形成,可以是一个直的圆柱形杆或一个连续的环或环来集中它们的磁通量。
电感器的原理图符号是一个线圈的符号,因此,一个线圈也可以称为电感的。电感器通常根据它们缠绕的内芯类型进行分类,例如,空芯(自由空气),实心铁芯或软铁氧体磁芯,不同的磁芯类型通过在旁边添加连续或虚线平行线来区分。线圈如下图所示。
电感符号

当前,流经电感器的i 产生与其成比例的磁通量。但不像电容器反对电路板上的电压变化,电感器反对由于磁场内自感能量的积累而流过电流的电流变化率。
字,电感器抵抗或反对电流的变化,但很容易通过稳态直流电流。电感器抵抗电流变化的能力以及电流 i 与其磁通量,NΦ作为比例常数的关系称为电感在Joseph Henry之后给出符号L,单位为亨利,(H)。
因为亨利本身就是一个相对较大的电感单位,对于较小的电感器,亨利的子单元用于表示其值。例如:
电感前缀
| 前缀 | 符号 | 乘数 | 10的幂 |
| milli | m | 1 / 1,000 | 10 -3 |
| 微 | μ | 1 /百万 | 10 -6 |
| 纳米 | 名词 | 1 /十亿 | 10 -9 |
因此,要显示亨利的子单位,我们将以此为例: / p>
1mH = 1 milli-Henry - 等于亨利的千分之一(1/1000)。
100μH= 100微亨利 - 等于1百万分之一(1 / 1,000,000)亨利。
电感器或线圈在电路中非常常见有许多因素决定了线圈的电感,例如线圈的形状,绝缘的匝数电线,电线层数,匝间距,芯材的磁导率,磁芯的尺寸或横截面积等等,仅举几例。
电感线圈有中心核心区域( A ),每单位长度具有恒定的线圈数( l )。因此,如果 N 圈的线圈通过一定量的磁通量连接,Φ则线圈具有NΦ的磁链和任何电流流过线圈的( i )将在与电流相反的方向上产生感应磁通量。然后根据法拉第定律,这个磁通链的任何变化都会在单个线圈中产生自感电压:

其中:
N 是转数
A 是以m为单位的横截面积 2
Φ是Webers中的流量
μ是渗透率核心材料
l 是以米为单位的线圈长度
di / dt 是电流的安培变化率/秒
时变磁场感应的电压与产生电流的电流的变化率成正比,其中正值表示电动势增加,负值表示减少在emf。通过用 L 代替μN 2 A / l ,可以找到与自感应电压,电流和电感相关的公式,表示常数比例性称为线圈的电感。
电感中的磁通与流过电感的电流之间的关系如下:NΦ= Li 。由于电感器由一个导线线圈组成,然后减少上述方程式,得到自感应电动势,有时也称为线圈中感应的反电动势:
返回电感由电感生成

其中: L 是自感和 di / dt 当前变化的速度。

电感线圈
所以从这个等式中我们可以说“自感电动势=电流变化电流”和电路的电感为1亨利将在电路中感应出一伏电压,当流过电路的电流以每秒一安培的速率变化时。
关于上述等式的一个重要注意事项。它只是将电感器两端产生的电动势与电流的变化联系起来,因为如果电感电流的流量是恒定的并且没有变化,例如在稳态直流电流中,那么感应的电动势电压将为零,因为瞬时电流变化率是零, di / dt = 0 。
当稳态直流电流流过电感器并因此在其上产生零感应电压时,电感器充当等于一条线的短路,或者至少是非常低的电阻值。换句话说,电感器提供的电流流动的反对在交流和直流电路之间是非常不同的。
电感的时间常数
我们现在知道电流不能在电感中瞬间改变,因为要发生这种情况,电流需要在零时间内改变一个有限的量,这将导致电流变化率无限, di / dt = ∞,使得感应电动势也是无限的,并且不存在无限电压。但是,如果流过电感的电流变化非常快,例如开关的操作,则可以在电感线圈上感应出高电压。

考虑右侧电感的电路。通过开关( S1 )打开,没有电流流过电感线圈。由于没有电流流过电感,线圈中的电流变化率( di / dt )将为零。如果电流变化率为零,则电感线圈内没有自感电动势( V L = 0 )。
如果我们现在关闭开关(t = 0),电流将流过电路并以由电感器的电感确定的速率缓慢上升到其最大值。流过电感的电流速率乘以Henry的电感电感,导致线圈产生一些固定值的自感电动势,如上面的法拉第方程所确定的, V L = Ldi / dt 。
电感线圈上的这种自感电动势( V L )与施加的电压作斗争,直到电流达到最大值并达到稳态条件。由于电流变化率( di / dt )在稳定状态下为零。换句话说,现在只存在线圈直流电阻以抵抗电流的流动。
同样,如果开关,(S1)打开,流过线圈的电流将开始下降但电感将会再次对抗这种变化,并试图通过在另一个方向上感应电压来保持电流流向其先前的值。下降的斜率将为负,并与线圈的电感相关,如下所示。
电感中的电流和电压

电感器产生多少感应电压取决于电流变化率。在我们关于电磁感应的教程中,Lenz定律指出:“感应电动势的方向是这样的,它总是会反对引起它的变化”。换句话说,感应电动势将始终取代首先启动感应电动势的运动或变化。
因此,随着电流减小,电压极性将充当电源并且电流增加电压极性将作为负载。因此,对于通过线圈的相同电流变化率,增加或减小感应电动势的幅度将是相同的。
电感器示例No1
稳态直流电4安培通过0.5H的电磁线圈。如果上述电路中的开关打开10mS并且流过线圈的电流降至零安培,那么线圈中感应的反电动势电压会是多少。

电感器中的功率
我们知道电路中的电感器通过它反对电流( i ),因为这个电流的流动会引起电动势反对它,楞次定律。然后必须通过外部电池电源完成工作,以保持电流流过这个感应电动势。用于强制电流( i )对抗这种自感电动势的瞬时功率( V L )从上面给出:

电路中的电源为, P = V * I 因此:

理想的电感器没有电阻,因此R =0Ω,因此线圈内没有功率耗散,所以我们可以说理想电感器的功率损耗为零。
电感器中的能量
当电源流入电感器时,能量存储在其磁场中。当流过电感的电流增加且 di / dt 大于零时,电路中的瞬时功率也必须大于零,( P> 0 )即正,这意味着能量存储在电感中。
同样,如果通过电感的电流减小且 di / dt 小于零,那么瞬时功率也必须小于零,( P <0 ),即负值,这意味着电感器将能量返回到电路中。然后通过积分上面的幂方程,总是正的,存储在电感中的总磁能量如下:
由电感器存储的能量

其中: W 以焦耳为单位, L 在Henries中, i 以安培为单位
能量实际上存储在流过电感器的电磁场内。在没有电阻或电容的理想电感中,当电流增加时,能量流入电感并在其磁场中存储而不会丢失,直到电流减小且磁场坍塌才会释放。
然后在交流电,交流电路中,电感器不断地存储并在每个周期传递能量。如果流过电感的电流在直流电路中是恒定的,则存储的能量没有变化,因为 P = Li(di / dt)= 0 。
因此,电感器可以定义为无源元件,因为它们既能存储又能为电路提供能量,但它们不能产生能量。理想的电感器被归类为损耗较少,这意味着它可以无限期地存储能量,因为没有能量损失。
然而,实际电感器总是会有一些与线圈绕组相关的电阻以及电流流过时无论电流是交流还是恒定,由于欧姆定律( P = I 2 R ),电阻能量以热量的形式损失。
然后,电感器的主要用途是滤波电路,谐振电路和电流限制。可以在电路中使用电感器来阻挡或重塑交流电流或一系列正弦频率,并且在这个角色中,电感器可以用于“调谐”简单的无线电接收器或各种类型的振荡器。它还可以保护敏感设备免受破坏性电压尖峰和高浪涌电流的影响。
在下一个关于电感器的教程中,我们将看到线圈的有效电阻称为电感,而电感就像我们现在一样知道电导体的特性“反对电流的变化”,可以是内部感应的,称为自感或外部感应,称为互感。
-
线圈
+关注
关注
14文章
1829浏览量
44479 -
电感器
+关注
关注
20文章
2332浏览量
70554
发布评论请先 登录
相关推荐
对电容和电感的时间常数表达
rc电路时间常数的定义及计算
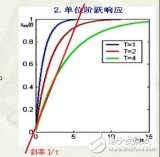
电路时间常数怎么求
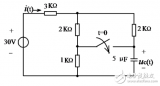
开关电源001--时间常数





 电感器的符号及时间常数
电感器的符号及时间常数
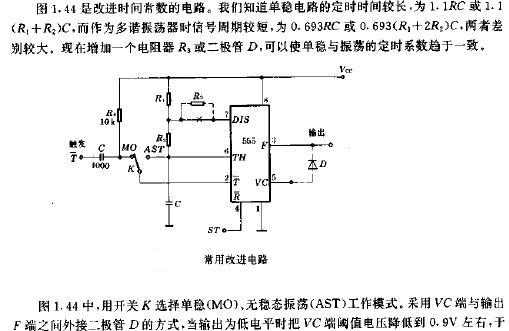
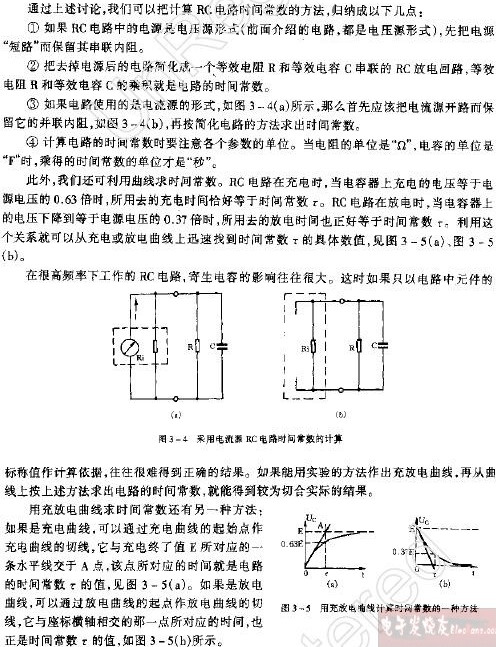











评论