二进制到十进制数字转换使用加权列来标识数字的顺序以确定数字的最终值
将二进制转换为十进制(base-2到base-10) )数字和背面是一个重要的概念,因为二进制编号系统构成了所有计算机和数字系统的基础。
十进制或“denary”计数系统使用Base-of-10编号系统,其中数字中的每个数字都取10个可能值中的一个,称为“数字”,从 0 到 9 ,例如。 213 10 (二百一十三)。
但是,除了10位数(0到9)之外,十进制编号系统还具有加法运算( + ),减法( - ),乘法(×)和除法(÷)。
在十进制系统中,每个数字的值都比其前一个数字大十倍,这个十进制数字系统使用一组符号 b ,以及一个基数 q ,确定一个数字内每个数字的权重。例如,六十分之六的权重低于六百分之六。然后在二进制编号系统中,我们需要一些方法将十进制转换为二进制以及从二进制转换为十进制。
任何编号系统都可以通过以下关系总结:
| N = b i q i | |
| where: |
N 是一个实数正数 b 是数字 是基数值 和整数( i )可以是正数,负数或零 |
N = b n q n ... b'的子> 3 q 3 + b <子> 2 q 2 + b <子> 1 q 1 + b <子> 0 q 0 + b <子> -1 q -1 + b -2 q -2 ... etc。
十进制编号系统
在十进制中, base-10(den)或denary编号系统,当我们沿着从右到左的数字移动时,每个整数列具有单位,数十,数百,数千等的值。在数学上,这些值写为10 0 ,10 1 ,10 2 ,10 3 等。然后每个位置在小数点左边表示增加的正幂为10.同样,对于小数,当我们从左向右移动时,数字的权重变得更负,10 -1 ,10 -2 ,10 -3 等
所以我们可以看到“十进制编号系统”的基数为10或 modulo-10 (有时称为MOD-10),十进制系统中每个数字的位置表示该数字的大小或重量为 q 等于“10”(0到9)。例如,20(二十)与说2 x 10 1 相同,因此400(四百)与说4 x 10 2 相同。
任何十进制数的值将等于其数字之和乘以各自的权重。例如: N = 6163 10 (六千一百六十三)十进制格式等于:
6000 + 100 + 60 + 3 = 6163
或者可以写出反映每个数字的权重:
(6×1000)+(1×100)+(6×10)+(3×1)= 6163
或它可以用多项式形式写成:
(6×10 3 )+(1×10 2 )+(6× 10 1 )+(3×10 0 )= 6163
在此十进制编号系统示例中,最左边的数字是最高有效数字或MSD,最右边的数字是最低有效数字或LSD。换句话说,数字 6 是MSD,因为它的最左侧位置承载的权重最大,而数字 3 是LSD,因为它的最右侧位置承载的权重最小。
二进制编号系统
二进制编号系统是所有基于数字和计算机的系统中最基本的编号系统,二进制数遵循相同的设置规则作为十进制编号系统。但是与使用10的幂的十进制系统不同,二进制编号系统使用2的幂,给出从base-2到base-10的二进制到十进制的转换。
数字逻辑和计算机系统仅使用两个用于表示条件,逻辑电平“1”或逻辑电平“0”的值或状态,并且每个“0”和“1”被认为是2的基数(bi)中的单个数字或“二进制编号系统“。
在二进制编号系统中,二进制数字如 101100101 用字符串”1“和”0“表示,每个数字沿字符串从右到左的值是前一个数字的两倍。但由于它是二进制数字,因此它只能具有“1”或“0”的值,因此 q 等于“2”(0或1),其位置表示其重量字符串。
由于十进制数是一个加权数,从十进制转换为二进制(基数10到基数2)也会产生加权二进制数,右边最多位为最低有效位或LSB,最左边的位是最高有效位或MSB,我们可以代表这个:
二进制数的表示
| MSB | 二进制数字 | LSB | ||||||
| 2 8 | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
我们在上面看到,在十进制数系统中,每个数字从右到左的权重增加了10倍。在二进制数系统中,权重如图所示,每个数字增加了一个因子 2 。然后第一个数字的权重为 1 ( 2 0 ),第二个数字的权重为 2 ( 2 1 ),第三个是 4 的重量( 2 2 ) ,第四个是 8 ( 2 3 )的权重,依此类推。
例如,转换二进制到十进制数字将是:
| 十进制数字值 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 二进制数字值 | 1 | 0 | 1 | <跨度> 1 | 0 | 0 | <跨度> 1 | 0 | 1 |
加在一起在由“ 1 ”表示的位置从右到左的所有十进制数值给出:(256)+(64)+(32)+(4)+(1)= 357 10 或三百五十七作为十进制数。
然后,我们可以通过查找二进制的十进制等效值将二进制转换为十进制数字数组 101100101 2 并将二进制数字扩展为基数为 2 的系列,其等效值为 357 10 十进制或否定。
请注意,在数字转换系统中,“下标”用于表示相关的基本编号系统,1001 2 = 9 10 。如果在数字后没有使用下标,则通常假设成为小数。
重复除2方法
我们已经看到上面如何将二进制数转换为十进制数,但我们如何将十进制数转换为二进制数。将十进制数转换为二进制数等效的简单方法是写下十进制数并连续除以2(二)得到结果,并给出“1”或“0”的余数直到最终结果等于零。
例如。将十进制数 294 10 转换为等效的二进制数。
| Number | 294 |
如图所示,将每个十进制数除以“2”将得到一个结果加上一个余数。 如果被分割的十进制数是偶数,那么结果将是整数并且余数将等于“0”。如果十进制数是奇数,那么结果将不会完全分割,余数将为“1”。 二进制结果是通过将所有余数按最低有效位(LSB)排序得到的位于顶部,最重要位(MSB)位于底部。 |
|
| 除以2 | |||
| 结果 | 147 | 余数 | 0(LSB) |
| 除以2 | |||
| 结果 | 73 | 余数 | 1 |
| 除以2 | |||
| 结果 | 36 | 余数 | 1 |
| 除以2 | |||
| 结果 | 18 | 余数 | 0 |
| 除以2 | |||
| 结果 | 9 | 余数 | 0 |
| 除以2 | |||
| 结果 | 4 | 余数 | 1 |
| 除以2 | |||
| 结果 | 2 | 余数 | 0 |
| 除以2 | |||
| 结果 | 1 | 余数 | 0 |
| 除以2 | |||
| 结果 | 0 | 余数 | 1(MSB) |
这种除以2的十进制到二进制转换技术给出十进制数 294 10 相当于 100100110 2 二进制,从右到左阅读。这种2分频方法也适用于转换为其他数字基础。
然后我们可以看到二进制编号系统的主要特征是每个“二进制数字” “或”位“具有”1“或”0“的值,每个位的权重或值是从最低位或最低位(LSB)开始的前一位的两倍,这称为”总和“权重“方法。
因此我们可以通过使用权重和方法或使用重复的2分频方法将十进制数转换为二进制数,并将二进制数转换为十进制通过查找其权重和。
二进制数字名称&amp;前缀
二进制数可以加在一起,也可以像十进制数一样减去,结果根据所使用的位数组合成几个大小范围之一。二进制数有三种基本形式 - 位,字节和字,其中一位是单个二进制数字,一个字节是八位二进制数字,一个字是16位二进制数字。
分类将各个位分成更大的组通常由以下更常见的名称引用:
| 二进制数字位数(位) ) | 通用名称 |
| 1 | 位 |
| 4 | 半字节 |
| 8 | 字节 |
| 16 | Word |
| 32 | 双字 |
| 64 | Quad Word |
此外,从 Binary转换为Decimal 或甚至从 Decimal转换为Binary ,我们需要注意不要混淆两组数字。例如,如果我们在页面上写入数字10,如果我们假设它是十进制数字,它可能意味着数字“十”,或者它可能同样是二进制中的“1”和“0”,这是等于上面加权十进制格式中的数字2。
在将二进制数转换为十进制数并确定所使用的数字或数字是十进制数还是二进制数时,要克服此问题的一种方法是在最后一位数字后写一个称为“下标”的小数字,以显示该数字的基数正在使用的数字系统。
因此,例如,如果我们使用二进制数字串,我们将添加下标“2”来表示基数为2,因此数字将写为 10 <子> 2 。同样,如果它是标准十进制数,我们将添加下标“10”来表示基数为10的数字,因此该数字将写为 10 10 。
今天,随着微控制器或微处理器系统变得越来越大,现在将各个二进制数字(位)组合成8个,形成单个 BYTE 与大多数计算机硬件如硬驱动器和内存模块通常以兆字节或甚至千兆字节表示其大小。
| 字节数 | 通用名称 |
| 1,024(2 10 ) | 千字节(kb) |
| 1,048,576(2 20 ) | 兆字节(Mb) |
| 1,073,741,824(2 30 ) | 技嘉(Gb) |
| a非常长的数字!(2 40 ) | 太字节(Tb) |
二进制到十进制摘要
A“ BIT “是源自 BI nary digi T
十进制系统使用10个不同的数字,0到9给它一个10的基数
二进制数是加权值从右到左增加的加权数
二进制数字的权重从右到左翻倍
十进制数可以通过使用权重和方法或重复的二分法来转换为二进制数
当我们转换时数字从二进制到十进制,或十进制到二进制,下标用于避免错误
将二进制转换为十进制(base-2到base-10)或十进制到二进制数(base10到base) -2)可以通过如上所示的多种不同方式完成。将十进制数转换为二进制数时,重要的是要记住哪个是最低有效位( LSB ),哪个是最高有效位( MSB )。
在下一个关于二进制逻辑的教程中,我们将研究将二进制数转换为十六进制数,反之亦然,并显示二进制数可以用字母和数字表示。
-
二进制
+关注
关注
2文章
801浏览量
41796 -
十进制
+关注
关注
0文章
67浏览量
13292
发布评论请先 登录
相关推荐


十进制和二进制之间的转换原理
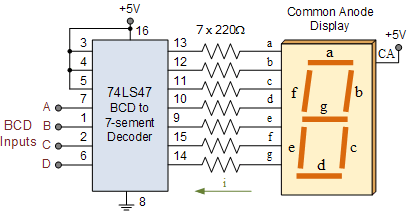
PIC16f877a MPlab组件 ADC结果显示在七段
二进制与十进制数对照显示实验,十进制,二进制对照
二进制编码的十进制表示转换解码器




 二进制如何转换为十进制?
二进制如何转换为十进制?










评论