二进制分数的使用

二进制分数使用与十进制数相同的加权原则，除了每个二进制数字使用base-2编号系统

我们知道十进制（或 denary ）数字使用十进制（基数为10）编号系统，其中十进制数中的每个数字都允许采用0到9范围内的十个可能值中的一个。因此，沿着十进制数从右向左移动，每个数字将它的值比其右边的数字大十倍。

但是当我们从右向左移动时，每个数字都比前一个数字大十倍，每个数字也可以是当我们从左到右沿相反方向移动时，它比它的相邻数字小十倍。

然而，一旦我们达到零（0）和小数点，我们不需要只停止，但可以继续沿着数字从左到右移动，产生通常称为分数。

典型的分数

这里以小数（或单数）数字为例，小数点右边的数字（数字5）值为小数点左边数字的十分之一（1/10或0.1）作为乘法值为1（1）的点（数字4）。

因此，当我们从左到右移动数字时，每个后续数字将立即成为数字值的十分之一

然后十进制编号系统使用位置或相对加权值的概念产生位置表示法，其中每个数字代表不同的加权值，取决于任何一侧占据的位置小数点。

因此在标准的否定编号系统中数学上，这些值通常写为：4 0 ，3 1 ，2 2 ，1 3 对于上面示例中小数点左边的每个位置。同样，对于小数点右边的小数，数字的权重变得更负，给出：5 -1 ，6 -2 ，7 - 3 等。

因此我们可以看到标准十进制系统中的每个数字都表示该数字内该数字的大小或重量。那么任何十进制数的值将等于其数字的总和乘以它们各自的权重，因此对于上面的示例：加权小数中的 N = 1234.567 10 格式也是相同的：

1000 + 200 + 30 + 4 + 0.5 + 0.06 + 0.007 = 1234.567 10

或者可以编写以反映每个否定数字的权重：

（1×1000）+（2×100）+（3×10）+（4×1）+（ 5×0.1）+（6×0.01）+（7×0.001）= 1234.567 10

或甚至以多项式形式表示：

<跨度>（1×10 3 ）+（2×10 2 ）+（3×10 1 ）+（4 ×10 0 ）+（5×10 -1 ）+（6×10 -2 ）+（7×10 - 3 ）= 1234.567 10

我们也可以使用这种位置表示法的概念，其中每个数字代表不同的加权值取决于它在二进制编号系统中占据的位置。这次的不同之处在于二进制数系统（或简称二进制数）是一个位置系统，其中数字的不同加权位置是2的幂（base-2）而不是10。

二进制分数

二进制编号系统是base-2编号系统，只包含两个数字，“0”或“1”。因此，二进制数的每个数字可以取“0”或“1”值，其中0或1的位置表示其值或加权。但是我们也可以对小于1的值进行二进制加权，产生所谓的无符号小数二进制数。

与小数小数类似，二进制数也可以通过将二进制数放入到无符号小数中来表示小数点的右边或在这种情况下，二进制点。因此，二进制点右侧的所有小数位具有各自的权重，其为2的负幂，从而产生二进制分数。换句话说，2的幂是负的。

因此对于二进制点右边的小数二进制数，每个数字的权重变得更负，给出：2 -1 ，2 -2 ，2 -3 ，2 -4 ，依此类推。

二进制分数

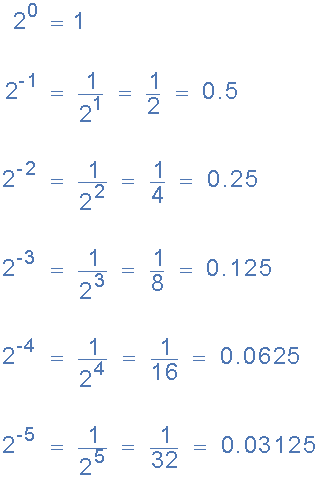
等等

因此，如果我们采用0.1011的二进制分数 2 然后考虑每个数字的位置权重，给出其十进制等值：

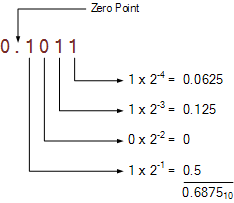
对于此示例，二进制数0.1011 2 的小数部分转换为0.6875 10 。

二进制分数示例No1

现在假设我们有以下二进制数： 1101.0111 2 ，它的等效十进制数是多少。

<跨度> 1101.0111 =（1×2 3 ）+（1×2 2 ）+（0×2 1 ）+（1×2 0 ）+（0×2 -1 ）+（1×2 -2 ）+（1×2 -3 ）+（1×2 -4 ）

<跨度> = 8 + 4 + 0 + 1 + 0 + 1/4 + 1/8 +16分之1

<跨度> = 8 + 4 + 0 + 1 + 0 + 0.25 + 0.125 + 0.0625 = 13.4375 10

因此， 1101.0111 2 给出如下：13.4375 10

所以我们可以看到分数二进制数，即加权小于1的二进制数（2 0 ），可以通过将2的幂的每次减少的二进制加权因子连续除以2来转换成它们的十进制数当量，同时记住2 0 等于1，

其他二元分数实例

0.11 =（1×2 -1 ）+（1×2 - 2 ）= 0.5 + 0.25 = 0.75 <子> 10

<跨度> 11.001 =（1×2 1 ）+ （1×2 0 ）+（1×2 -3 ）= 2 + 1 + 0.125 = 3.125 <子> 10

<跨度> 1011.111 =（1×2 3 ）+（1×2 1 ）+（1×2 0 ）（1×2 -1 ）+（1×2 -2 ）+（1×2 -3 ）

=8+2+1+0.5+0.25+0.12 5 = 11.875 10

将十进制转换为二进制分数

使用a将小数部分转换为小数二进制数类似于我们用于整数的方法。但是，这个时间乘法用而不是用整数除法而不是用于进位数的余数是十进制数的小数部分的二进制等价。

当从十进制转换为二进制时，整数（正序从右到左）部分和十进制数的小数（从左到右的部分）部分是单独计算的。

对于数字的整数部分，二进制等价通过连续地将（称为连续除法）十进制数的整数部分重复地除以2（÷2），从最低有效位（LSB）到最高有效位（MSB）以相反的顺序记录剩余部分，直到找到该值变为“0”，产生二进制等价。

所以要找到十进制整数的二进制等值： 118 10

118 （除以2）= 59plus余数0（LSB）

59 （除以2）= 29plus剩余nder1（↑）

29 （除以2）= 14plus余数1（↑）

14 （除以2）= 7plus余数0（↑ ）

7 （除以2）= 3plus余数1（↑）

3 （除以2）= 1plus余数1（↑）

1 （除法by 2）= 0plus余数1（MSB）

然后二进制当量 118 10 因此： 1110110 2 ←（LSB）

通过连续乘法（称为连续乘法）找到数字的小数部分将十进制数的小数部分重复2（×2），以正向顺序记录进位，直到该值变为“0”，产生二进制等价。

因此，如果乘法过程产生的产品更大如果乘法过程产生的产品小于“1”，则进位为“1”进位是“0”。

另请注意，如果连续的乘法过程似乎没有朝向最终的零，则小数将具有无限长度或直到相等的位数已经获得，例如8位。或者16位等等，具体取决于所需的精度。

所以要找到等效小数的二进制分数： 0.8125 10

0.8125 （乘以2）=1.625 = 0.625carry1（ MSB）

0.625 （乘以2）=1.25 = 0.25carry1（↓）

0.25 （乘以2）=0.50 = 0.5carry0（↓）

0.5 （乘以2）=1.00 = 0.0carry1（ LSB）

因此， 0.8125 10 的二进制当量是： 0.1101 2 ← （LSB）

我们可以使用上面的步骤仔细检查这个答案，将二进制分数转换成等效的十进制数： 0.1101 = 0.5 + 0.25 + 0.0625 = 0.8125 10

二进制分数示例No2

查找等效于以下十进制数的二进制分数： 54.6875

首先我们使用从上面的连续除法以正常方式将整数54转换为二进制数。

54 （除以2）= 27remainder0（LSB）

27 （除以2）= 13remainder1（↑）

13 （除以2）= 6rem ainder1（↑）

6 （除以2）= 3remainder0（↑）

3 （除以2）= 1remainder1（↑）

1 （除以2）= 0remainder1（MSB）

因此二进制当量因此， 54 10 ： 110110 2

接下来我们将小数部分转换为0.6875使用连续乘法得到二进制分数。

0.6875 （乘以2）=1.375 = 0.375carry1（MSB）

0.375 （乘以2）=0.75 = 0.75carry0（↓）

0.75 （乘以2）=1.50 = 0.5carry1（↓）

0.5 （乘以2）=1.00 = 0.0carry1（LSB）

因此， 0.6875 10 的二进制等效值是： 0.1011 2 ←（LSB）

因此二进制等效的十进制数： 54.6875 10 是 110110.1011 2

二元分数摘要

我们在本教程中已经看到二元分数将任何小数部分转换为等效的二进制分数，我们必须将小数部分乘以小数部分，并将小数部分乘以2并记录数字出现在二进制点的左侧。这个二进制数字是进位数字，总是为“0”或“1”。

然后我们必须将剩余的小数部分乘以2再次使用连续乘法重复上述序列直到分数对于重复的二进制分数，已经减少到零或者已经完成了所需的二进制位数量。分数由2的负幂表示。

对于混合十进制数，我们必须执行两个单独的运算。小数点左边的整数部分的连续除法和小数点右边的小数部分的连续乘法。

请注意，混合十进制数的整数部分将始终具有精确值二进制数等价，但小数部分可能不等，因为如果我们想要精确地表示小数部分，我们可以得到一个重复分数，产生无限数量的二进制数字。