布尔代数使用一组定律和规则来定义数字逻辑电路的操作
以及用于表示数字的逻辑符号“0”和“1”输入或输出,我们也可以将它们分别用作永久“开放”或“封闭”电路或接触的常数。
已经发明了一组规则或布尔代数表达式的法则来帮助减少执行特定逻辑运算所需的逻辑门数量导致一系列函数或定理通常称为布尔代数定律。
布尔代数是我们用来分析数字门和电路的数学。我们可以使用这些“布尔定律”来减少和简化复杂的布尔表达式,以减少所需的逻辑门数。因此,布尔代数是一个基于逻辑的数学系统,它具有自己的一套规则或定律,用于定义和减少布尔表达式。
布尔代数中使用的变量只有两个可能值中的一个,逻辑“0”和逻辑“1”,但表达式可以有无数个变量,所有变量都单独标记以表示表达式的输入,例如,变量A,B,C等,给出了A + B = C的逻辑表达式,但每个变量只能是0或1。
这些的例子布尔代数的布尔,规则和定理的各个定律在下表中给出。
布尔定律的真值表
|
Boolean Expression |
描述 |
等效 切换电路 |
布尔代数 法律或规则 |
| A + 1 = 1 |
A平行于 closed =“CLOSED” |
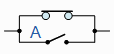 |
Annulment |
| A + 0 = A |
A与 open =“A” |
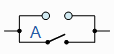 >> >> |
Identity |
| A. 1 = A |
A与 关闭=“A” |
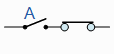 |
标识 |
| A。 0 = 0 |
A与 open =“OPEN”串联 |
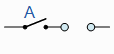 |
Annulment |
| A + A = A |
A并行与 A =“A” |
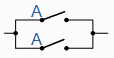 |
幂等 |
| A。 A = A |
A与 A =“A”串联 |
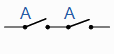 |
幂等 |
| NOT A = A |
NOT NOT A (double negative)=“A” |
双重否定 | |
| A + A = 1 |
A与 A = “CLOSED” |
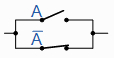 |
补充 |
| A。 A = 0 |
A系列与 NOT A =“OPEN” |
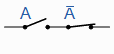 |
补充 |
| A + B = B + A |
A并行B = B与A |
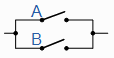 |
交换 |
| AB = BA |
与B = B与A串联 |
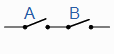 |
交换 |
| A + B =A.B | 将AND替换为OR | de Morgan's定理 | |
| AB = A + B | 反转并且用OR替换AND | de Morgan定理 |
布尔代数的基本定律与交换法有关,允许改变加法和乘法的位置,联想法允许删除加法和乘法的括号,以及分配允许表达式分解的定律与普通代数相同。
每个o f上面的布尔定律仅用一个或两个变量给出,但由单一定律定义的变量数量不限于此,因为可以有无数个变量作为输入表达。上面详述的这些布尔定律可用于证明任何给定的布尔表达式以及简化复杂的数字电路。
下面给出了各种布尔定律的简要描述,其中 A 表示变量输入。
布尔代数定律的描述
废除法 - 术语 AND 与“0”等于0或 OR 与“1”等于1
A. 0 = 0 变量AND与0总是等于0
A + 1 = 1 变量OR 'ed with 1总是等于1
身份法 - 术语 OR 带有“0”或 AND 带“1”将始终等于该术语
A + 0 = A 与0进行OR运算的变量始终等于变量
A. 1 = A 变量AND与1总是等于变量
幂等律 - AND '或 OR 与自身的输入等于输入
A + A = A 变量与自身进行“或”运算始终等于变量
A. A = A 与自身进行AND运算的变量始终等于变量
补充法 - 术语 AND ,其补码等于“0”,术语 OR '其补码等于“1”
A. A = 0 变量与其补码的AND'总是等于0
A + A = 1 与其补码相关的变量OR总是等于1
交换法 - 两个单独术语的应用顺序并不重要
A. B = B. A 两个变量AND'的顺序没有区别
A + B = B + A 订单其中两个变量是OR的没有区别
双重否定法律 - 反转两次的术语等于原始术语
A = A 变量的双重补码始终等于变量
de Morgan's Theorem - 有两个”de Morgan's“规则或定理,
(1)两个单独的术语 NOR '在一起与两个术语倒置(补语)和 AND '例如: A + B = A 。 B
(2)两个单独的术语 NAND '在一起是s ame作为两个术语倒置(补语)和 OR '例如: AB = A + B
上面未详述的布尔的其他代数定律包括:
分配法 - 该法允许表达式的乘法或分解。
A(B + C)= AB + AC (或分配法)
A +(BC)=(A + B)。(A + C)(和分配法)
吸收法 - 这项法律通过吸收类似的术语,可以将复杂的表达式简化为更简单的表达式。
A +(AB)= A (或吸收定律)
A(A + B)= A (和吸收定律)
联想法 - 该法允许从表达式中删除括号并重新组合变量。
A +(B + C)=(A + B)+ C = A + B + C(OR Associate Law)
A(BC)=(AB)C = A. B。 C(AND Associate Law)
布尔代数函数
使用上面的信息,简单的2输入AND,OR和NOT门可以用16种可能的函数表示,如下表所示。
2.
| 函数 | 描述 | 表达 |
| 1 | NULL | 0 |
| IDENTITY | 1 | |
| 3. | 输入A | A |
| 4. | 输入B | B |
| 5 。 | NOT A | A |
| 6。 | NOT B | B |
| 7. | A AND B(AND) | AB |
| 8. | A AND NOT B | A. B |
| 9. | NOT A AND B | A .B |
| 10. | NOT AND(NAND) | AB |
| 11. | A OR B(OR) | A + B |
| 12. | A OR NOT B | A+B |
| 13. | 不是A或B | A + B |
| 14. | NOT OR(NOR) | A + B |
| 15 | 异或 | A. <跨度>乙 + <跨度> A .B |
| 16 | 异NOR | A·B + A 。 B |
布尔代数的定律示例No1
使用上述定律,简化以下表达式:(A + B)(A + C)
| Q = | (A + B)。(A + C) | |
| AA + AC + AB + BC | - 分配法 | |
| A + AC + AB + BC | - 幂等与法律(AA = A) | |
| A(1 + C)+ AB + BC | - 分配法 | |
| A.1 + AB + BC | -Identity OR law(1 + C = 1) | |
| A(1 + B)+ B.C | - 分配法 | |
| A.1 + B.C | - 身份或法律(1 + B = 1) | |
| Q = | A +(B.C) | - 身份和法律(A.1 = A) |
然后表达式:(A + B )(A + C)可简化为 A +(BC),如分配法。
-
布尔代数
+关注
关注
0文章
11浏览量
7893 -
数字逻辑
+关注
关注
0文章
74浏览量
16748
发布评论请先 登录
相关推荐
逻辑代数基础
基尔霍夫定律及其应用
基尔霍夫的电压定律和能量守恒分析
关于代数攻击中代数免疫的若干性质分析
逻辑代数的基本定律和规则
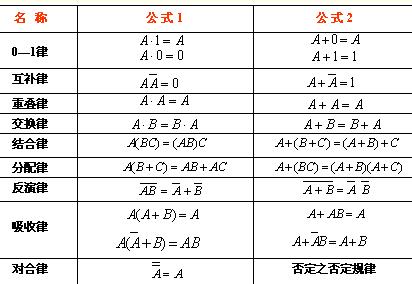




 布尔代数定律的描述
布尔代数定律的描述












评论