基尔霍夫的现行法律

基尔霍夫的电流定律（KCL）是基尔霍夫的第一个定律，用于处理进入和离开结的电荷守恒。

确定电流周围的电流量或大小或电子电路，我们需要使用某些法律或规则，允许我们以等式的形式记下这些电流。所使用的网络方程式是根据基尔霍夫定律的方程式，当我们处理电路电流时，我们将研究基尔霍夫的当前定律（KCL）。

Gustav Kirchhoff的现行定律是用于电路分析的基本定律之一。他的现行法律规定，对于并联路径，进入电路结的总电流恰好等于离开相同结的总电流。这是因为它没有其他地方可以去，因为没有电荷丢失。

换句话说，所有进入和离开结点的电流的代数和必须等于零：ΣI IN =ΣI OUT 。

基尔霍夫的这个想法通常被称为充电守恒，因为电流在结点周围保守而没有电流损失。让我们看一下Kirchhoff当前定律（KCL）应用于单个连接点的简单示例。

单个连接点

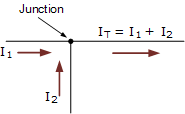
这个简单的单结示例中，离开结点的电流 I T 是两个电流的代数和， I 1 和 I 2 进入同一个交叉点。那是 I T = I 1 + I 2 。

请注意我们可以也正确地将其写为代数和： I T - （I 1 + I 2 ）= 0 。

所以，如果我 1 等于3安培且I 2 等于2安培，那么总电流I T 离开结点将是3 + 2 = 5安培，我们可以将此基本定律用于任意数量的结点或节点，因为进入和离开的电流总和将相同。

此外，如果我们颠倒了电流的方向，对于I 1 或I 2 ，得到的方程仍然适用。当我 1 = I T -I 2 = 5-2 = 3安培，I 2 = I T -I 1 = 5-3 = 2安培。因此，我们可以将进入结点的电流视为正（+），而离开结点的电流为负（ - ）。

然后我们可以看到电流的数学总和要么进入或者离开交叉点并且在任何方向上总是等于零，这形成了基尔霍夫连接规则的基础，更常见的是基尔霍夫的当前定律或（KCL）。

并联电阻

让我们看看我们如何将Kirchhoff的电流定律并联应用于电阻，无论这些分支中的电阻是相等还是不相等。请考虑以下电路图：

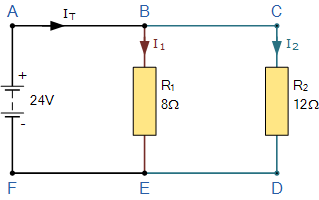
在这个简单的并联电阻器示例中，有两个不同的电流结。结点1发生在节点B处，结点2发生在节点E处。因此，我们可以使用基尔霍夫结点规则来处理这两个不同结点的电流，对于那些进入结点的电流以及流向结点的电流。 / p>

首先，所有电流，I T 离开24伏电源并到达A点，然后从那里进入节点B.节点B是一个结，因为电流现在可以分成两个不同的方向，一些电流向下流动并通过电阻器R 1 ，其余部分继续通过电阻器R 2 通过节点C继续。注意电流流动进入和离开节点通常称为分支电流。

我们可以使用欧姆定律来确定通过每个电阻的各个分支电流：I = V / R，因此：

对于电流分支B至E，通过电阻R 1

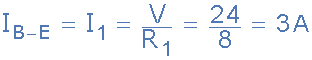
对于电流分支C至D通过电阻R <子> 2

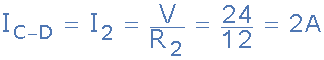
从上面我们知道基尔霍夫的现行定律表明，进入结的电流之和必须等于离开结的电流之和，在上面的简单例子中，有一个电流I T 进入节点B的结点，两个电流离开结点，I 1 ，I 2 。

由于我们现在从计算中知道离开节点B处的结的电流是I 1 等于3安培而I 2 等于2安培，进入节点B的结点的电流必须等于3 + 2 = 5安培。因此Σ IN = I T = 5安培。

在我们的例子中，我们在节点B和节点E有两个不同的连接点，因此我们可以确认I T 的这个值，因为两个电流在节点E再次重新组合。因此，对于Kirchhoff的连接规则保持为真，进入F点的电流之和必须等于流出的电流之和节点E的连接点。

由于进入结E的两个电流分别为3安培和2安培，因此进入F点的电流之和为：3 + 2 = 5安培。因此Σ IN = I T = 5安培，因此基尔霍夫电流定律成立，因为它与当前离开点A的值相同。

将KCL应用于更复杂的电路。

我们可以使用基尔霍夫电流定律来找到在更复杂电路周围流动的电流。我们希望现在知道节点（连接点）处的所有电流的代数和等于零，并且考虑到这个想法，这是确定进入节点和离开节点的电流的简单情况。考虑下面的电路。

基尔霍夫的现行法律例子No1

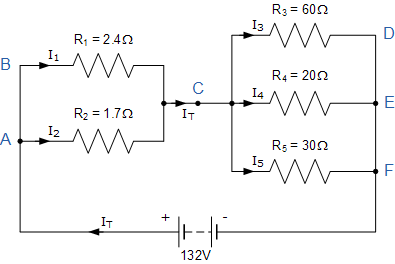
在这个例子中是电流在节点A，C，E和节点F处分开或合并在一起的四个不同的结点。电源电流I T 在流过电阻器R 1 和R 2 ，在节点C重新组合，然后再次通过电阻器R 3 ，R 4 和R 5 分离最后在节点F再次重新组合。

但在我们计算流过每个电阻支路的各个电流之前，我们必须首先计算电路总电流I T 。欧姆定律告诉我们I = V / R并且我们知道V的值，132伏，我们需要计算电路电阻如下。

电路电阻R AC

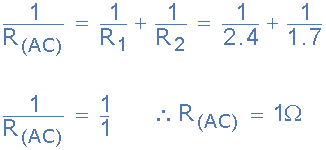
因此节点A和C之间的等效电路电阻计算为1欧姆。

电路电阻R CF

>

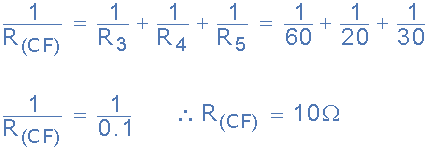
因此节点C之间的等效电路电阻并且F计算为10欧姆。然后总电路电流I T 给出如下：

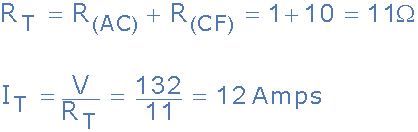
给我们一个等效电路：

基尔霍夫电流定律等效电路

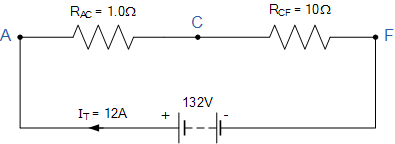
因此，V = 132V，R AC =1Ω，R CF =10Ω，I T = 12A。

建立等效并联电阻和电源电流后，我们可以现在计算各个分支电流并使用Kirchhoff的连接规则确认如下。

因此，我 1 = 5A，I 2 = 7A，I 3 = 2A，I 4 = 6A，I 5 = 4A。

我们可以通过使用节点C作为我们的参考点来计算进入和离开结点的电流，确认Kirchoff的电流定律适用于电路：

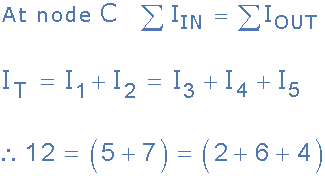
我们还可以仔细检查Kirchhoffs Current Law是否适用，因为进入交叉点的电流是正的，而离开的是周四，路口是负面的代数和是：I 1 + I 2 -I 3 -I 4 -I 5 = 0等于5 + 7 - 2 - 6 - 4 = 0.

因此我们可以通过分析证实基尔霍夫电流定律（KCL）表明电流的代数和在这个例子中，电路网络中的连接点始终为零是正确的。

基尔霍夫电流定律示例No2

使用基尔霍夫电流定律求出在后续电路周围流动的电流仅

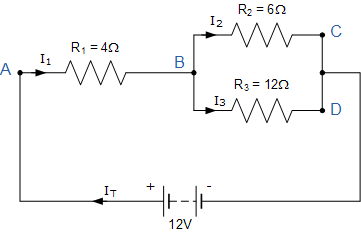
I T 是由12V电源电压驱动的电路周围的总电流。在A点， I 1 等于 I T ，因此会有 I 1 * R 电阻R 1 上的电压降。

该电路有2个分支，3个节点（B，C和D）和2个独立的循环，因此两个循环周围的I * R电压降将是：

循环ABC⇒12= 4I 1 + 6I 2

循环ABD⇒12= 4I 1 + 12I 3

由于基尔霍夫现行法律规定在节点B处， I 1 = I 2 + I 3 ，因此我们可以用两个当前的I 1 代替（I 2 + I 3 ）跟随循环方程，然后简化。

基尔霍夫环路方程

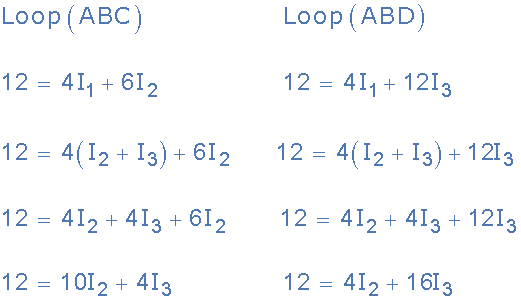
我们现在有两个与在电路周围流动的电流有关的联立方程。

Eq。否1： 12 = 10I 2 + 4I 3

等式No 2： 12 = 4I 2 + 16I 3

将第一个等式（循环ABC）乘以4并且从循环ABC中减去Loop ABD，我们可以减少这两个方程，得到 I 2 和 I 3 的值

等式否1： 12 = 10I 2 + 4I 3 （x4）⇒ 48 = 40I 2 + 16I <子> 3

等式No 2： 12 = 4I 2 + 16I 3 （x1）⇒ 12 = 4I 2 + 16I <子> 3

等式没有1-Eq。否2⇒ 36 = 36I 2 +0

用术语替换 I 2 of I 3 为我们提供 I 2 的值为 1.0Amps

现在我们可以通过将第一个等式（循环ABC）乘以4和第二个等式（Loop）来执行相同的过程来找到 I 3 的值再次通过从Loop ABD中减去Loop ABC，我们可以减少两个方程，得到 I 2 和 I 的值3

等式否1： 12 = 10I 2 + 4I 3 （x4）⇒ 48 = 40I 2 + 16I <子> 3

等式否2： 12 = 4I 2 + 16I 3 （x10）⇒ 120 = 40I 2 + 160I <子> 3

等式没有2-Eq。否1⇒ 72 = 0 + 144I 3

因此替换 I 3 in术语 I 2 为我们提供 I 3 的值为 0.5Amps

正如Kirchhoff的交叉规则所述： I 1 = I 2 + I 3

流过电阻器 R 1 的电源电流如下： 1.0 + 0.5 = 1.5Amps

因此 I 1 = I T = 1.5Amps ， I 2 = 1.0Amps 和 I 3 = 0.5Amps 根据该信息，我们可以计算出器件和电路周围各点（节点）的I * R压降。

我们可以简单而简单地使用欧姆定律解决了示例二的电路，但我们在这里使用基尔霍夫电流定律来说明如何解决更复杂的电路当我们不能简单地应用欧姆定律时。