网格电流分析是一种用于在电路的任何闭合路径中找到在环路或网格周围循环的电流的技术。
虽然基尔霍夫定律为我们提供了基本方法分析任何复杂的电路,通过使用网格电流分析或节点电压分析,可以通过不同的方法改进这种方法,从而减少所涉及的数学运算网络涉及这种数学减少可能是一个很大的优势。
例如,考虑上一节中的电路示例。
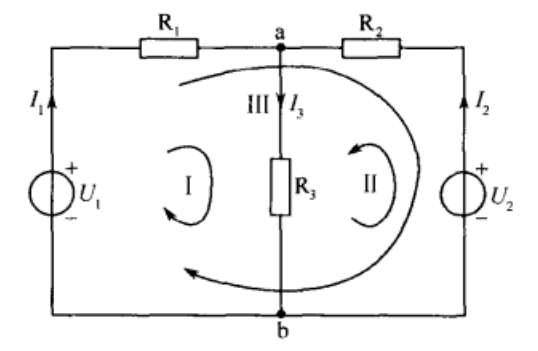
网状电流分析电路
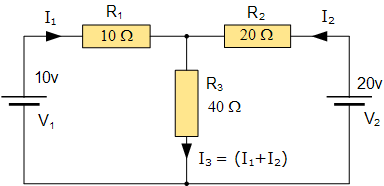
减少数学量的一种简单方法是使用基尔霍夫电流定律方程分析电路,以确定电流, I 1 和 I 2 流入两个电阻器。然后,无需计算当前 I 3 ,因为它只是 I 1 和 I <子> 2 。因此,基尔霍夫的第二个电压定律变为:
等式1: 10 = 50I 1 + 40I 2
公式2: 20 = 40I 1 + 60I 2
因此,已经保存了一行数学计算。
网格电流分析
解决上述电路的一种更简单的方法是使用网格电流分析或循环分析,有时也称为Maxwell的循环电流方法。我们需要用循环电流标记每个“闭环”,而不是标记分支电流。
作为一般的经验法则,只有顺时针方向的环路标记,循环电流的目标是覆盖电路的所有元件至少一次。任何所需的分支电流都可以从适当的环路或网状电流中找到,如前所述使用Kirchhoff方法。
例如:: i 1 = I 1 ,I <子> 2 = - I 2 和<跨度> I <子> 3 = I 1 -I 2
我们现在以与以前相同的方式编写Kirchhoff的电压定律方程来解决它们,但这种方法的优点是它确保了从电路方程获得的信息是求解电路所需的最小信息,因为信息更通用,并且可以很容易地以矩阵形式存储。
例如,考虑前一节中的电路。
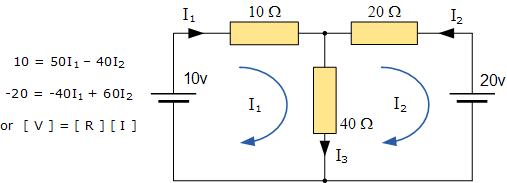
使用单个网格阻抗矩阵 Z 可以非常快速地解决这些方程。主对角线上的每个元素将是“正”,并且是每个网格的总阻抗。其中,每个元素OFF主要对角线将为“零”或“负”,并表示连接所有相应网格的电路元素。
首先我们需要理解在处理矩阵时,对于两个矩阵的除法与将一个矩阵乘以另一个矩阵的倒数相同,如图所示。
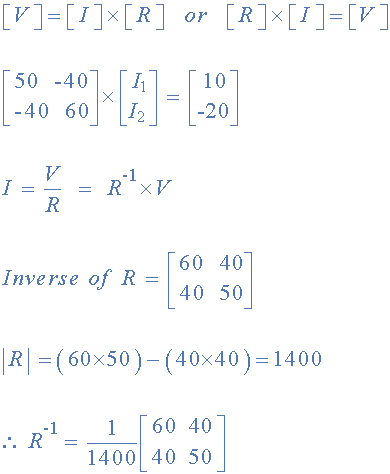
找到 R 的倒数,因为 V / R 与 V x R -1 ,我们现在可以用它来找到两个循环电流。
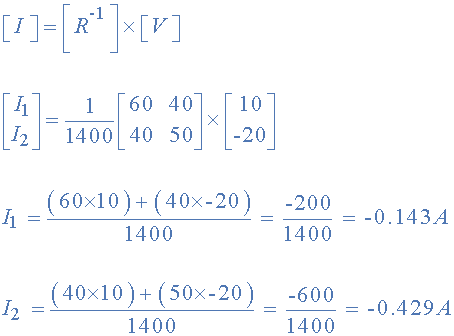
其中:
[V] 给出环路1的总电池电压,然后是环路2
[I] 表示我们试图找到的回路电流
[R] 是电阻矩阵
[R -1 ] 是[R]矩阵的反转
,这使 I 1 为 - 0.143Amps 和 I 2 as -0.429Amps
As: I 3 = I 1 -I 2
因此给出了 I 3 的组合电流as: -0.143 - ( - 0.429)= 0.286Amps
这是 0.286amps 的相同值,我们发现使用Kirchoff的电路定律在上一个教程中。
网格电流分析摘要
电路分析的这种“观察”方法可能是所有电路分析方法中最好的,具有解决的基本程序网格电流分析方程式如下:
1。用循环电流标记所有内部环路。 (我 1 ,我 2 ,...我 L 等)
2.写入[ L x 1 ]列矩阵[ V ],给出每个回路中所有电压源的总和。
3。为电路中的所有电阻写入[ L x L ]矩阵[ R ],如下所示:
R 11 =第一个循环中的总阻力。
R nn =第N个循环中的总电阻。
R JK =直接将循环J连接到循环K的电阻。
4。写入矩阵或向量方程 [V] = [R] x [I] 其中 [I] 是要找到的电流列表。
除了使用网格电流分析,我们还可以使用节点分析计算环路周围的电压,再次使用基尔霍夫定律减少所需的数学量。在下一个与直流电路理论相关的教程中,我们将研究节点电压分析。
-
电路
+关注
关注
173文章
5980浏览量
173153 -
电流
+关注
关注
40文章
6951浏览量
132829
发布评论请先 登录
相关推荐
无线网状网络的路由协议分析
接地电路电流采样反馈分析
如下电流检测电路具体是怎么分析的?
电流模式开关电源中斜坡补偿电路的分析与设计
蓝牙网状网络的四大优点分析




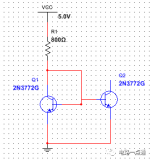
 网状电流分析电路
网状电流分析电路










评论