导读:生活中我们处处面临最优化的问题,比如,怎么样一个月减掉的体重最高?怎么样学习效率最高?怎么样可以最大化实现个人价值?
显然,每一个目标都受很多因素的影响,我们称之为目标函数的最优化。
优化的思路有很多种,比如基于梯度的梯度下降,基于二阶梯度的牛顿法,基于近似的二阶梯度的拟牛顿法,基于下界函数的最优化,贪婪算法,坐标下降法,将约束条件转移到目标函数的拉格朗日乘子法等等。
本文我们讨论一下基于下界函数的最优化,且将讨论的范围限定为无约束条件的凸优化。
基于下界函数的优化
在有些情况下,我们知道目标函数的表达形式,但因为目标函数形式复杂不方便对变量直接求导。这个时候可以尝试找到目标函数的一个下界函数,通过对下界函数的优化,来逐步的优化目标函数。
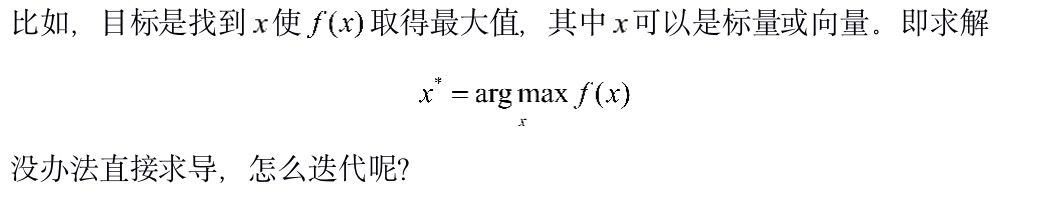



上面的描述性推导很是抽象,下面我们来看两个具体的例子,EM算法和改进的迭代尺度法。限于篇幅,我们重点推导EM算法,改进的迭代尺度法只是提及一下。
EM算法



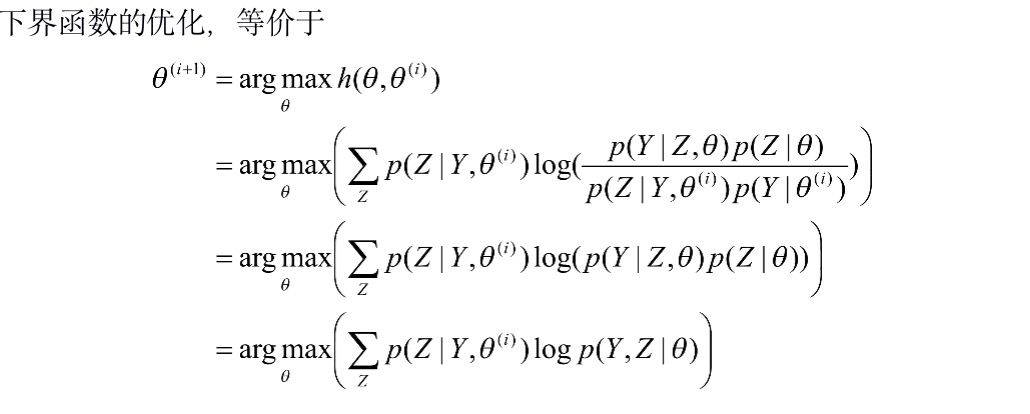
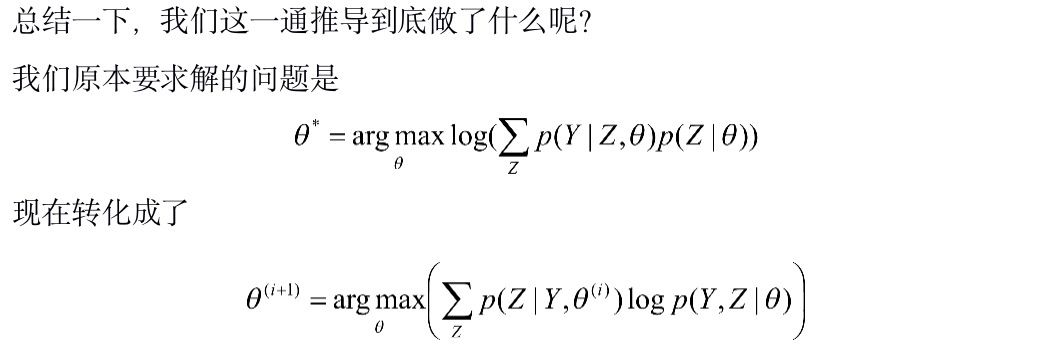



改进迭代算法
概率模型中最大熵模型的训练,最早用的是通用迭代法GIS(Generalized Iterative Scaling)。GIS的原理很简单,大致包括以下步骤:
假定初始模型(第0次迭代)为等概率的均匀分布。
用第k次迭代的模型来估算每种信息特征在训练数据中的分布,如果超过了实际的,就把相应的模型参数变小;反之,将参数变大。
重复步骤2,直到收敛。
GIS算法,本质上就是一种EM算法,原理简单步骤清晰,但问题是收敛太慢了。Della Pietra兄弟在1996年对GIS进行了改进,提出了IIS(Improved Iterative Scaling)算法。IIS利用log函数的性质,以及指数函数的凸性,对目标函数进行了两次缩放,来求解下界函数。详情可参阅李航的《统计学习方法》一书。
小结
本文讨论了一下基于下界函数的最优化这样一种优化思路,希望对大家有所帮助。同时也一如既往地欢迎批评指正,以及大神拍砖。
-
算法
+关注
关注
23文章
4636浏览量
93509 -
函数
+关注
关注
3文章
4350浏览量
63090
原文标题:优化思路千万种,基于下界函数的最优化效率如何?
文章出处:【微信号:rgznai100,微信公众号:rgznai100】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
一种基于经优化算法优化过的神经网络设计FIR滤波器的方法介绍
labview数据的组合排序最优化
粒子群算法城镇能源优化调度问题
一种求解非线性约束优化全局最优的新方法
一种解决函数优化问题的免疫算法
Matlab最优化方法

一种具有全局快速寻优的多学科协同优化方法

一种小生境灰狼优化算法
一种语义规则为指导的增量优化方法
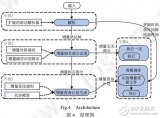
一种改进灰狼优化算法的用于求解约束优化问题
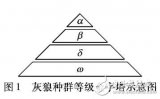




 基于下界函数的最优化这样一种优化思路
基于下界函数的最优化这样一种优化思路










评论