GNN在普适性与学习局限性等问题

【导读】GNN是目前机器学习领域的热门网络之一，肯多研究与技术分享相比不可知的深度学习网络模型，GNN 有哪些吸引我们的优势及硬核实力。然而，GNN 是完美的吗？有什么缺点？在何种情况下，GNN 是无法发挥其能力的？近日，在 arXiv 上发布了一篇论文，专门研究探讨了 GNN 在普适性与学习局限性等问题。

本文主要从计算能力有限的角度，来研究GNN在消息传递分布式系统中的图灵普适性和局限性，并得到了两个与图论问题能否解决（impossibility statements）有关的结论：

（1）在一定的充足条件下，GNN是具有图灵普适性的；

（2）而在深度和广度被限制的条件下，GNN的性能会有一定的局限性。

应用第一个结论，可以对一些图论优化问题设置更低的计算复杂度下界，第二个结论则说明在深度和广度的乘积不超过图的大小时，GNN是无法解决其他的一些问题的。

专业术语

为了方便大家后续阅读理解文章，我们先把文中涉及的几个专业问题做简单阐述：

1、图灵普适性（Turing universal）

一个具有图灵普适性的图灵机（Universal Turing machine）能够模拟任何图灵机在任何输入下的情况。

2、一致性问题（Consensus）

即在分布式计算或者多代理（multi-agent）系统中，如何在发生进程故障的情况下保持系统的可靠性（reliability）。这通常需要进程就计算过程中的一些数值或数值操作达成一致，包括如何将提交到数据库，如何识别leader进程，状态机复制（一种故障容忍机制），原子广播等操作。

3、不可能结果（Impossibility result）

这是分布式领域的专业术语，在一个完全异步的消息传递分布式系统中，如果一个进程有故障，那么一致性问题是无法得到解决的，在此基础上，有两个比较著名的 impossibility result：FLP和CAP，详见[1][2]。本文中提出了关于GNN的两个结论都是属于GNN的 impossibility results。简单来说，就是在一定的限制条件下问题能否被解决，那么任务的impossibility result就只有两种情况：能和不能。

4、GNN的深度和广度（depth and width）

深度就是网络层数，广度就是每层的感知域，也就是每个节点的能获取到信息的邻接节点的范围。

模型普适性的研究

机器学习中的一个基本任务是研究哪些内容是一个模型（网络）能学习到，而哪些是不能学习到的，也就是研究模型的普适性，研究其能否解决大部分任务。过去的一些研究通过不变函数或者等效函数来对网络进行等效近似，从而在函数层面研究什么是一个模型能学习到的内容。

通常理论认为，在有充足的训练数据和合适的学习优化算法的情况下，普适性网络能够解决大部分给定的任务，然而这种理解是不全面的，因为在实际应用时要满足充足训练数据和合适优化算法是比较困难的，这种无限制的普适性网络是不能作为实际部署时的网络设计参考的。

因此，可以从问题的对立面，即研究模型的局限性，来间接地研究其普适性，也就是在特定的任务中，特定的限制条件下网络不能学习到的内容。这有助于了解模型和特定任务之间的关系，从而知晓任务能否被解决（impossibility results），进而帮助我们调整模型的参数。例如，在图分类任务中，我们希望模型能学习到同一类图的共同特征，不同类图的区别特征，然而如果GNN模型本身的深度和广度不足以学习到足够的特征，那么这个问题就是impossible的，因此就需要进一步的调整深度和广度。

文章主要贡献

本文所研究的特定任务是图论中的一些优化任务，特定限制条件是 GNN 的深度和广度，将深度和广度与理论计算机科学中的复杂度等度量联系起来，再将计算复杂度作为这些优化任务的完成下界（从 impossible 变为 possible 的最低复杂度要求），从而得到GNN的深度和广度对具体任务的影响，以及对GNN普适性的影响。具体地，关于普适性的研究有以下两个结论。

1、GNN 的图灵普适性

在足够的条件下，GNN 能以图灵机的形式对任意输入函数进行运算，且不限于网络结构。通过建立 GNN 和经典分布式计算模型 LOCAL 之间的图灵等效，来间接的研究其普适性。这里的足够条件是：

（1）有足够的层数

（2）每一层都有足够的广度

（3）节点之间可以相互独立（ids）

（4）每一层计算的函数有足够的表现力

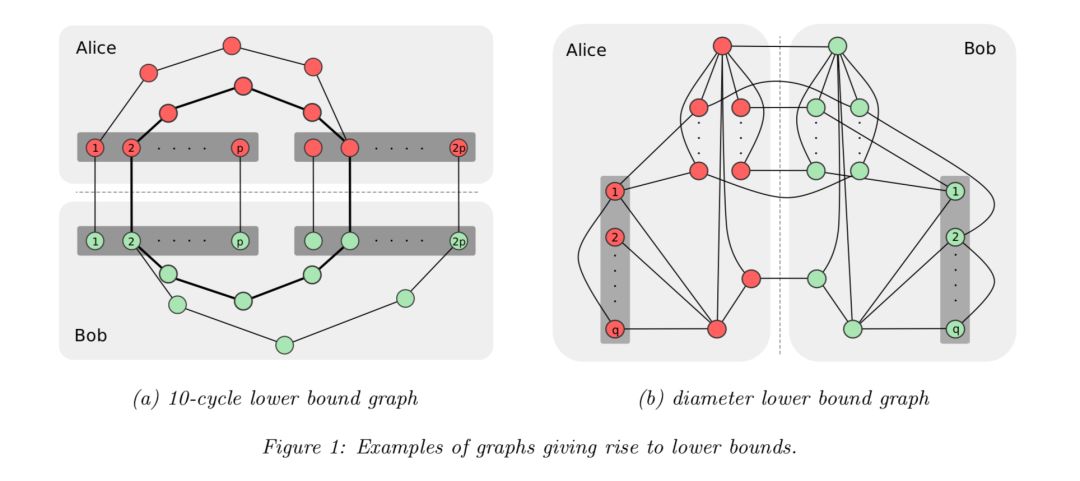
2、GNN 的学习能力局限性

正如前面提到的，在深度和广度都被限制的情况下，GNN是无法表现出其图灵普适性，即应用在具体任务上时，无法解决这个任务。那么如何确定能否完成任务的下界呢？还是通过 LOCAL。任务或问题的 impossiblility result 可以在GNN和LOCAL之间以一定的形式相互转换，因此研究任务在 GNN下能否完成和在LOCAL下能否完成是等效的，进而可以在LOCAL模型下为完成任务的计算复杂度要求设置下界。具体的，文章中提到了四种类型的任务（问题定义详见原论文）：

（1）检测（detecting）图G中是否含有特定长度的环（cycle of specific length）

（2）验证（verifying）图G的给定子图是否连通（connected），是否具有环（cycle），是否为生成树（spanning tree，具备树结构，没有环），是否为二分图（bipartite，顶点集合可以分为两个子集，所有边的两个顶点分属于这两个子集），是否为简单路径（simple path，与图的哈密顿循环有关）

（3）计算（computing）两个顶点间的最短路径（shortest path between two vertices），图的最小割（minimum cut），以及最小生成树（the minimum spanning tree）

（4）求图的最大独立集（maximum independent），最小顶点覆盖（minimum vertex cover），或图的顶点着色问题（chromatic coloring）

以上问题都是属于图论中的传统优化问题，虽然不是现在主流研究的顶点分类，图分类问题，但二者之间有密不可分的联系。这些问题的具体计算复杂度下界为：

总结

本文首次对GNN模型提出了 impossible 问题，并通过等效计算的方法，以计算复杂度的形式，给出了 GNN 在部分图论任务中impossible results下界与网络宽度和广度的关系，在一定程度上说明了 GNN 的性能会受到网络本身的宽度和广度的限制。

由于原文中的数学推导过于复杂，因此这里我只介绍文章的基本思想。GNN作为目前机器学习领域的热门研究之一，已经被应用于各种各样的任务，通常在应用一个网络的同时，也要同步地去研究这个网络的内在本质，从而更好的理解，改进它，进而帮助我们在实际应用网络时更好的设置网络的参数，这篇文章就是一个很好的例子。