一、引言
近几年来,在伺服应用系统领域中对各种转速的要求提高了人们对开关磁阻电机(简称SRM)的兴趣。主要原因还是由于SRM具有结构简单、成本低、运行可靠、低速转矩大、简单的功率转换电路、控制方式灵活和效率高等优点。虽然SRM在过去的几年里有了很大发展,但仍存在一些问题有待研究,如与一般电机相比其转距脉动比较明显,这就限制了其在伺服传动系统中的应用。为了使SRM能在伺服领域中发挥其固有的优点,研究如何有效的抑制SRM低速转矩脉动具有十分重要的意义。在这方面各国学者做了大量的研究,有人提出按在饱和运行时产生近似正弦的转矩/转角静态特性来优化电动机的结构设计,并且采用伺服电动机控制器产生正弦的希望电流/转角分布,以此削弱瞬时转矩脉动。文献[1]中采用模糊自适emerging SRM.应控制方案,模糊参数从开始的自由选择到最后调整为最优。文献[2]中采用局部逼近的神经网络,对期望的电流波形进行在线学习,从而实现转矩脉动的最小化。但上述方法并没得到广泛的实际应用,其原因主要是其控制方案复杂,难以实时控制。
本文中通过借鉴步进电机细分驱动技术,结合分析SRM矩角特性为本文的控制策略提供理论上的依据,并在实验过程中验证了控制策略的实效性,达到实验的目的,有效地减小转矩脉动,并使噪声大大减小。
二、微分驱动的原理
在步进电机的驱动控制中,将电机绕组中的电流对应各个平衡位置进行细分,由常规的矩形波供电改成阶梯波供电,绕组中的电流经过若干个阶梯上升到额定值或者从额定值经过若干个阶梯下降到零。经过细分后,驱动电流的变化幅度大大减小。故转子到达平衡位置时的过剩能量也大为减少;另一方面,控制信号的频率提高了N倍(细分数),故可远离转子的低频谐振频率。因此,运用细分驱动不仅能使电机运行平稳,而且还能减弱或消除振荡引起的低频噪声。
从上述可以看出,步进电机的细分实质是在电机各相绕组的电流切换时代替原来的绕组电流直接通断的方法。对于SRM而言,其工作原理与大角度步进电动机相似,定子磁动势在空间以一个较大的步进角步进运行,由此我们考虑到在SRM驱动中是否也可以借鉴步进电机细分驱动的思想,在换相时细分绕组电流使通过绕组的电流阶梯变化,通过控制各相电流的大小使绕组转矩矢量在转子的各平衡位置保持大小基本恒定,即减小了转矩脉动。
三、SRM转矩矢量控制原理
在SRM矩角特性分析中,若忽略磁路的非线性因素影响,电磁转距可表示为:

式中L为SRM相绕组的直感,忽略高次谐波,相绕组自感为:
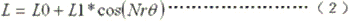
式中:L0、L1为自感的恒定分量和基波分量的幅值,可以认为是常数。Nr为SRM转子齿数
由(1)、(2)可得:
T(θ,i)=-Tmax*sin(Nrθ)……………………(3)
所以,每相绕组产生的基波电磁转矩是一种空间正弦波,稳定零位取决于该相磁极中心线的位置。电磁转矩是转子位置θ和相电流的函数。因此,可以用空间矢量TA代表A相绕组的电磁转矩,其相位和A相绕组磁极中心线一致。在开关磁阻电机步进运动分析中,旋转磁场转矩矢量图可以使分析形象化,在本文的分析中以(8/6)四相SR电动机为例,如图1。
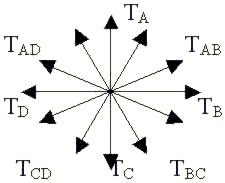
图1 SRM旋转磁场转矩矢量
对于(8/6)四相SR电动机而言,A相绕组产生的稳定零位和B相绕组产生的稳定零位错开一个步进角,在空间按几何角度15度,若用电角度表示90度。如规定转子顺时针方向旋转为正转,则只要按A-B-C-D的顺序依次给各相绕组供电,开关磁阻电动机的转子以步进角15度一步一步的正转。假定忽略电动机的互感,允许将转矩进行矢量相加,即得到图1所示的旋转磁场转矩矢量,其中TAB 、TBC、TCA和TAD称为派生转矩矢量,表示两相同时供电的合成转矩;TA、TB、TC、TD称为基本转矩矢量,他们相位取决于定子磁极中心线的空间位置,表示一相单独供电时的转矩,相临两个转矩错开步进角3.75度。派生转矩和基本转矩的关系可表示为下列向量形式:
TAB=TA+TB…………………………(4)
派生转矩矢量的相位可以通过对绕组电流幅值的控制加以调节,使它出现在基本转矩矢量之间的任何相位上,采用控制绕组电流的办法增加SRM的每转步数,提高分辨率,减小转矩脉动。随着电动机每转细分步数的增加,可供选择的最佳离散电流波形为正弦函数波形,如果能够控制各相绕组的电流为正弦波,则实现SRM的连续控制。
四、微分驱动在SRM控制系统中的实现
由以上对(8/6)SRM转矩控制原理的分析可知,开关磁阻电机细分驱动的核心就是为了实现转矩矢量幅值相等,控制相绕组电流跟随给定转速对应的给定电流大小,使实时转速保持在给定转速误差范围内,从而有效减小了转矩的脉动。
同时导通的两相绕组电流可表示为下式,式中为合成矢量对应的电流大小:
ia=Im*cosθ;
ib=Im*sinθ; ………………………………………(5)
则合成电流矢量i(以ia为参考):
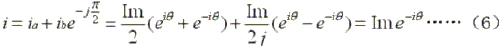
i是一个以Im为幅值,-θ为辐角的矢量。这样,由式(1)、(6)可知,每当θ的值发生变化时,合成的矢量转过一个相应的角度,且幅值大小保持不变,实现了恒力矩的细分驱动。利用式(5)可得到细分后通电相电流数据。
所以要控制转矩必须控制电流,而控制电流是以控制PWM功率变换器输出脉宽被调制的功率开关信号为直接控制量,使实际输出电流按阶梯波电流变化。因此SRM的微分驱动要靠控制PWM的占空比来实现。用下式表示加在导通相绕组的PWM信号的占空比:
Ya=Y*cosθ ;
Yb=Y*sinθ ;……………………………………(7)
上式中:Y为占空比幅值; Ya,Yb分别为Y在通电相绕组的分量;θ为转矩角;
(7)式中的占空比幅值Y与 速度闭环中的给定速度通过量化换算得出线性对应关系:
Y=k*n;k为比例系数;
所以在速度给定的前提下,占空比幅值Y保持恒定,由(7)式可知,只要调整特定平衡位置的转矩角即可控制各相PWM脉宽占空比分量,根据(5)式与(7)式的对应关系,由各相占空比分量大小的变化从而控制了导通相电流的大小。
(8/6)四相SRM转子极距角(周期)为60度,每相步进角为15度,因此微分驱动的行为即是要细分该15度的步进角,在15度的步进角中找到三个转矩平衡位置,由于SRM绕组电流的大小受PWM功率变换器控制,所以调节PWM输出脉宽即可使实际输出电流如图2所示按阶梯波电流变化,各相通电顺序为:
电机正转时:A-AB1-AB2-AB3-B-BC1-BC2-BC3-C-CD1-CD2-CD3-D-DA1-DA2-DA3-A
反转时:A-AD1-AD2-AD3-D-DC1-DC2-DC3-C-CB1-CB2-CB3-B-BA1-BA2-BA3-A
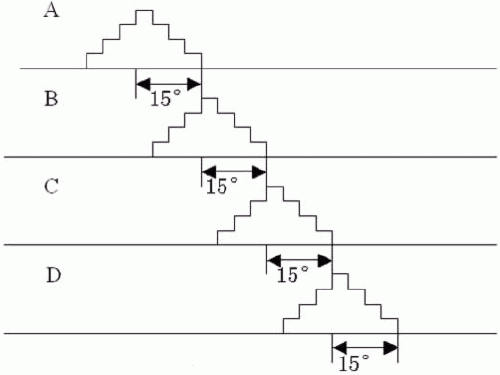
图2(8/6)SRM细分绕组理想电流波形
在SRM转子位置检测中,由光电旋转编码器检测转子位置产生较高分辨率的数字信号。如转子每旋转一周(360度)能产生N个信号,则称其为Np/r(脉冲/转)。把N个脉冲信号细分,每转过N/96个脉冲调整一次相绕组电流大小,使转子的一个大步距角细分成4个小的步距角。从而使电流用换相区代替换相点,即在换相时关断相电流不是立即关断到零,而是按阶梯下降;导通相也并不是立即导通,而是按阶梯逐渐导通。阶梯的宽度 即PWM脉宽占空比由32个脉冲转过的时间决定。
控制系统原理如图3所示,实际转速与给定转速相比较产生的偏差信号通过调节器经过PID运算产生给定转速对应PWM脉宽占空比Y,同时根据转子位置脉冲查表对应平衡位置转矩角θ对应的正余弦值,经过算术运算求得实时通电相PWM占空比幅度Ya、Yb,即控制了通过SRM绕组的有效电流大小。
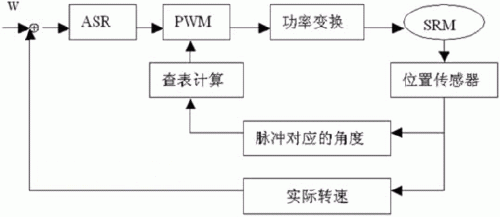
图3 SRM细分驱动控制原理图
五、实验与结论
本文论述的微分驱动SRM的控制策略在具体实施阶段,选用了Microchip公司的PIC18F2331高档八位单片机,该芯片内部集成了丰富的外设资源,其中功率控制PWM模块、CCP模块、A/D模块、光电编码器接口(QEI)等为SRM的控制提供了方便。
利用CCP模块的捕捉模式,当转子位置信息脉冲符合设定的条件时(上升沿或下降沿出现),中断标志位CCP1IF被硬件自动置位,产生一次CCP1捕捉中断。将TMR1的计数值传送到CCPR1寄存器。根据计数值可计算电机转速。
在PIC18F2331中,功率控制PWM模块支持三个PWM发生器和六个输出通道。在本系统中,功率变换部分采用半桥式电路,相与相之间完全独立,每相需要一个IGBT作为主开关器件,所以只要选用两个PWM发生器和四个输出通道即可满足电机的驱动控制。
A/D模块为10位高速转换器,可通过寄存器设置芯片的工作电压作为A/D转换的参考电压(即使用VCC为参考电压)。则模拟信号的输入范围为0~VREF。
相电流采样选用霍尔电流传感器采样电流信号,霍尔电流传感器本身已存在滤波电路,输出可直接提供给单片机的A/D模块。
在本控制系统中采用了光电编码器测量转子位置,作为闭环控制的反馈量。PIC18F2331提供了这种编码器的接口电路,编码脉冲通过2个引脚QEA和INDX 输入到芯片内部作为输入时钟,时钟信号使位置计数器寄存器(POSCNT)递增。此寄存器的工作模式决定了是在QEA 输入沿递增。如果与周期寄存器MAXCNT 匹配该寄存器复位。如果允许位置计数器中断,当POSCNT复位时会产生一个中断。
由于本系统采用了外设资源集成度比较高的PIC单片机,所以硬件电路比较简单。 系统框图如下:
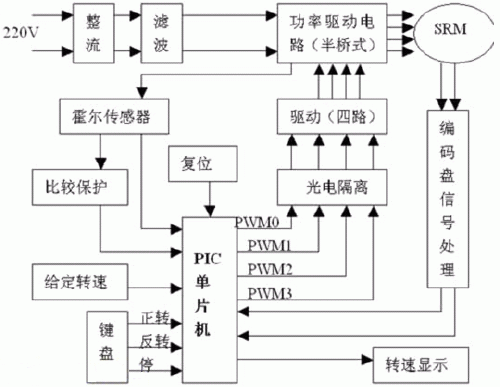
图4 系统框图
经过实验验证,该微分驱动控制方法使SRM最低可平稳运行在20r/min的转速,在低速运行状态下的转矩脉动大大减小,转动时的噪声也得到了有效的改善。
但是如果在感性负载的情况下,电动机中电流的上升或衰减并不是瞬时完成的。尤其在SRM高速运行时,绕组中电流只有很短的时间来跟踪给定,因此微步细分的步数和转速都受到一定程度的限制,并不能无限微步细分。
参考文献
[1] S. Mir, M.E. Elbuluk, I. Husain, Torque-ripple minimization in switched reluctance motors using adaptive fuzzy control, IEEE Trans. Industry Appl. 35 (2) (1999) 461_/468 (March/April).
[2] Reay D S , Green T C, Williams B W .Application of Associative Memory Neural Networks to the Control of a Switched Reluctance Motor[c].Proc.IECON’93,Maui,HI.
[3] 王宏华. 开关型磁阻电动机调速控制技术. 机械工业出版社, 1995.
[4] 王鸿钰,步进电机控制技术入门,1990.
[5] PIC18F2331/2431/4331/4431数据手册,Microchip Technology Inc.
[6] 刘和平等 PIC18FXXX单片机程序设计及应用,北京航空航天大学出版社,2005.
 电子发烧友App
电子发烧友App



















评论