采样控制系统时间响应特性及其计算方法

采样控制系统时间响应特性及其计算方法

    摘  要：本文针对采样控制系统连续信号与离散信号共存的特点，指出传统离散化分析方法因忽略了系统在采样时刻之间的信息导致无法精确、真实地反映采样控制系统的时间响应特性，在此基础上，应用采样控制系统直接设计方法，基于提升技术，在考虑系统在采样时刻之间全部信息的条件下，推导给出了采样控制系统时间响应的计算方法，最后通过一个具体计算实例说明了本文方法的有效性。
    关键词：采样控制系统  提升技术  时间响应

1 引言
    当前多数控制方案都采用离散控制器控制连续被控对象的方法，这就构成了采样控制系统［１］。连续时间信号和离散时间信号共存，是采样控制系统的显著特点，也成为精确分析采样控制系统的难点所在［２］。传统的采样控制系统时间响应的计算方法是将连续被控对象离散化后，应用离散系统理论近似计算系统的时间响应，这种计算方法的缺陷有两点：一是系统的真实输出为连续输出，而计算结果却是离散的；另外，计算过程中只考虑系统在采样时刻点的信息，却忽略了系统在采样时刻之间的信息，因此只能是一种不精确的计算方法。
??本课题受高等学校博士学科点专向科研基金资助(HB-097-6820)
    本文应用采样控制系统直接设计方法［２，３］，基于提升技术，推导给出了采样控制系统时间响应计算方法。
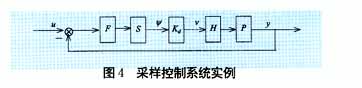
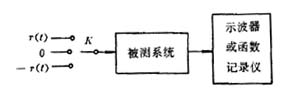
    标准采样控制系统的结构框图如图1所示，图中实线代表连续信号，虚线代表离散信号，y(t)为输出信号，u(t)为外部输入信号，ψ、ν为数字信号，Kd为线性时不变离散控制器，S、H分别为理想采样开关和保持器，G为广义连续LTI被控对象，可表示为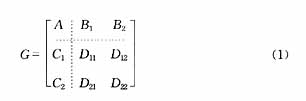

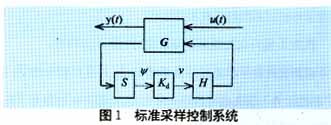
    由于采样开关的存在，使采样控制系统中连续和离散信号共存，具有周期时变性。Bassam A.Bamieh将采样控制系统进行提升化处理，提升后系统为离散时不变系统，其输入输出空间为无穷维，而系统范数不变［２，３］。可见，提升技术虽然解决了采样控制系统的周期时变问题，但提升后系统的输入输出空间是无穷维，这一问题成为采样控制系统分析和设计的主要难点。
2 采样控制系统时间响应特性及其计算方法
    本节应用提升技术将采样控制系统Ｆ转化为线性时不变系统F，然后求解系统F(G，Kd)的时间响应，得到提升输出。最后，将提升输出进行逆提升处理，从而得到采样控制系统的时间响应输出y(t)，如图2所示。

2.1 采样控制系统的提升化处理
    提升算子L和逆提升算子L－１的作用可做如下直观解释［２］：L将定义在t∈［０，＋∞)上的连续信号y分割成定义在k∈N上的无穷个离散信号yk，每一个离散信号取值于定义在［０，h)上的Banach空间；而L－１是将无穷个离散信号“粘贴”成连续信号，如图3所示，提升技术具有如下性质［４］：
    性质1：连续信号经过提升后，信号的范数保持不变，且L·L－１＝Ｉ。
    性质2：周期时变的采样控制系统经过提升化处理后变成输入输出空间为无穷维的线性离散时不变系统，且提升系统不改变采样控制系统的范数和稳定性。?
    性质3：提升化处理不改变系统的时间响应特性。
    根据提升算子和逆提升算子的定义，只是对信号的“分割”或“粘贴”，并不丢失信号的任何信息，因此提升化处理并不改变信号的时域特性，性质3显然成立，证明略。

    为使问题简化，设式(1)所示被控对象模型满足D２１＝Ｄ２２＝０，提升后采样控制系统中广义被控对象模型为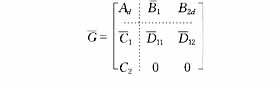


2.2 采样控制系统的时间响应特性
    提升系统的闭环状态空间表示为，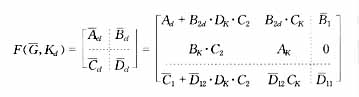

    由于提升系统是线性时不变离散系统，故系统的闭环状态空间表示为

    但［kh,(k+1)h)时间段内，由于B1u是定积分，因此是常值，同时区间［kh,(k+1)h)内却是变化的，所以在区间［kh,(k+1)h)内随时间t′变化。假设系统初态为零，对于任意时刻t(0≤t＜∞)，在输入信号u(t)作用下，系统的输出响应为

    可见根据式(2)，对于任意时刻t，都存在yk(t′)与之对应，所以由式(2)表示的采样控制系统时间响应是连续的，而且式(2)中，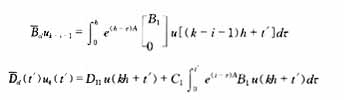

    以上算子表达式说明式(2)描述的采样控制系统的时间响应考虑了采样时刻之间系统的信息，并且在任意时变输入信号下，算子都具有精确解，这样，式(2)真实地反映了采样控制系统的时间响应特性。
2.3 采样控制系统时间响应计算方法

    当外部输入信号为任意时变信号时，算子的计算方法是首先将积分区间n等分，然后应用近似求和的方法计算积分项，n值选取越大，计算结果越精确，计算公式如下：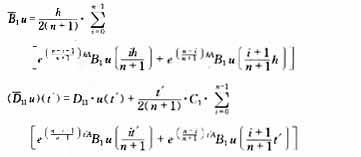



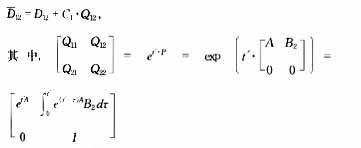
3 计算实例

　

    根据前述内容计算采样控制系统的时间响应，响应曲线如图5和图6所示。
    图5为单位阶跃信号下的响应曲线，图6为频率0.5?Hz、单峰1°的正弦输入下［０，５］秒内的输出响应，曲线1是应用本文方法计算出的时间响应曲线，由于考虑了采样时刻之间系统的信息，所以响应曲线是光滑曲线，而曲线2是首先将低通滤波器和连续被控对象离散化，得到纯离散系统后计算出的响应曲线，在一个周期［kh,(k+1)h)时间内，系统输出为常值，故响应曲线为阶梯状。

    另外，当t′＝０时，即只考虑采样时刻的响应时，若外部输入为常值，提升系统简化为通常的离散系统，故图5中曲线1与曲线2在采样时刻存在重合点；而当外部输入为任意时变信号时，由于离散系统理论认为在［kh,(k+1)h)区间内，外部输入信号为常值u(kh)，却没有考虑连续输入信号在［kh,(k+1)h)间内的变化，因而相对于真实系统的输出产生滞后，且随着采样周期增加，滞后变大。因此，图6中曲线2滞后于曲线1，即使在采样时刻点，两条曲线也不存在重合点。可见，基于提升技术计算出的采样控制系统时间响应输出更接近于真实系统。
4 结论
    本文应用提升技术，将周期时变的采样控制系统转化为线性时不变离散控制系统，然后求解出提升系统的时间响应，再经过逆提升处理，解算出采样控制系统的时间响应。这种方法的优点在于考虑了连续被控对象在采样时刻之间的动态性能，因此相比于传统采样控制系统时间响应的计算方法，更具实际意义。

参考文献：

［１］Bassam Bamieh,J.Boyd Pearson.A lifting technique for linear periodic systems with applications to sampled_data control［Ｊ］．System & Control Letters，1991,17:79-88
［２］Bassam Bamieh,J.Boyd Pearson.A General Framework for Linear Periodic Systems with Applications to H.∝. Sampled_data Control［Ｊ］.IEEE Trans AC，1992,37:418-435
［３］毕贞福.采样控制系统设计方法及其应用研究［Ｄ］．哈尔滨工业大学博士学位论文，1998
［４］T.Chen,B.A.Francis.Optimal Sampled_data Control Systems［Ｃ］．Springer_Verlag,1995