并联电阻的等效计算公式为:
1R =1R1 +1R2 +…+1Rn (1)
使用该公式时,有两种情况计算比较方便:
① 并联的电阻比较少时,如两个电阻并联时,一般都是直接由公式R=R1×R2R1+R2 求得等效电阻 ;
② 当并联的n个电阻阻值相等时,等效电阻为 R=R1n 。
但当多个电阻并联且电阻值又都不相等时,计算就比较烦琐,为此,本文对公式(1)进行了变形,使多个电阻的并联计算变得简化。
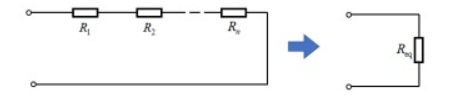
将公式(1)变形可得:
R= 1 1R1 +1R2 +…+1Rn = Ri RiR1 +RiR2 +…+RiRn = Ri K1+K2+…+Kn (2)
其中K1=RiR1 ,K2=RiR2 ,… Kn=RiRn ,Ri为n个并联电阻中的一个,Ri的选择可遵循如下的规则:
① 选能被其它电阻整除的一个电阻作Ri
例1 有三个电阻并联,R1=3Ω,R2=6Ω,R3=18Ω,则选电阻R3作为被除电阻Ri,即: K1=183 =6,K2=186 =3,K3=1818 =1
等效电阻 R=Ri K1+K2+K3 = 18 6+3+1 =2Ω
②当找不到一个电阻能被其它电阻整除时,选阻值最大的电阻作为被除电阻Ri 。
例2 三个电阻R1=8Ω,R2=10Ω,R3=12Ω并联,则选阻值最大的电阻R3=12Ω作为被除电阻Ri,计算就比较方便,此时有:
K1=128 =1.5,K2=1210 =1.2,K3=1212 =1
等效电阻 R=Ri K1+K2+K3 = 12 1.5+1.2+1 =12 3.7 =3.24Ω
当然,也可以任选一个电阻作为被除电阻Ri,但与选择阻值最大的电阻作为被除电阻时相比,计算时小数增多,增加了烦琐程度,甚至影响计算精度.
例如,例2中,选8Ω的电阻作为被除电阻Ri,则有:
K1=88 =1,K2=810 =0.8,K3=812 =0.67
得等效电阻 R=Ri K1+K2+K3 = 8 1+0.8+0.67 =8 2.47 =3.23Ω
可见,计算比上例烦琐,精度也有所降低.
③也可以选择n个电阻之外的任意一个阻值作被除电阻,这个电阻可以选成能被所有的n个电阻整除,这样计算更方便。
例如,例2中的三个电阻R1=8Ω,R2=10Ω,R3=12Ω并联时,可选一个能被三个电阻都整除的数值作被除电阻值,如选120Ω,则有:
K1=1208 =15,K2=12010 =12,K3=12012 =10
等效电阻
R= Ri K1+K2+K3 = 120 15+12+10 = 120 37 =3.24Ω
结果与例2一致,但计算中少了小数,更容易被接受。
公式(2)的物理意义,就是把所有的电阻都折算成电阻Ri的并联,共折算成K1+K2+…+Kn 个Ri的并联,如上述例1中把所有的电阻都折算成18Ω电阻的并联,将3Ω看作是6个18Ω的电阻并联,6Ω的电阻可看作3个18Ω的电阻并联。上述例2中把所有的电阻都折算成8Ω电阻的并联,10Ω电阻可看作0.8个8Ω的电阻并联,12Ω可看作0.67个8Ω的电阻并联.其中0.8个8Ω的电阻可以这样理解,将8Ω的电阻纵向剖成10份,每份的截面积是原来的十分之一,电阻是原来的十倍(80Ω),取其中的8份并联,即为0.8个8Ω的电阻并联.
综上所述,运用公式(2)计算等效电阻,比公式(1)简单,尤其是当并联的电阻较多时,分解了难点,计算显得更方便了。
 电子发烧友App
电子发烧友App









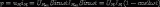




















评论