RLC串联谐振电路解析，RLC串联谐振仿真

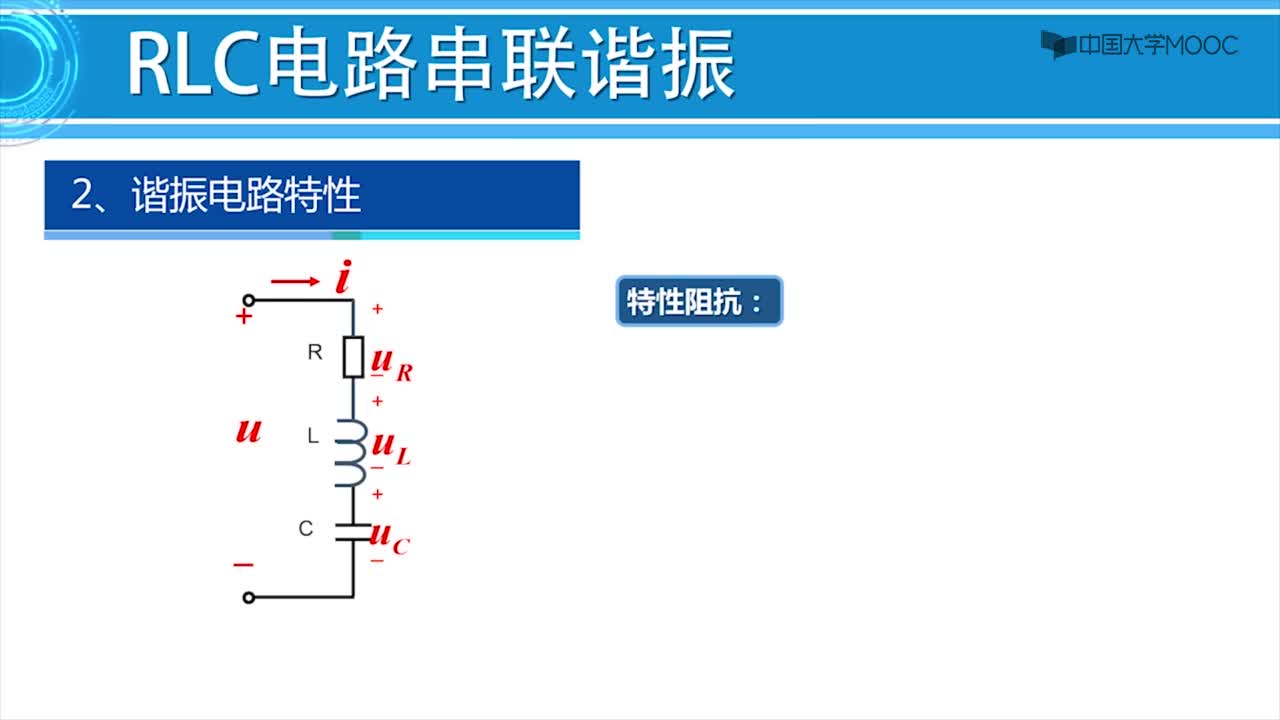
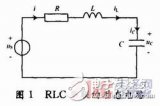
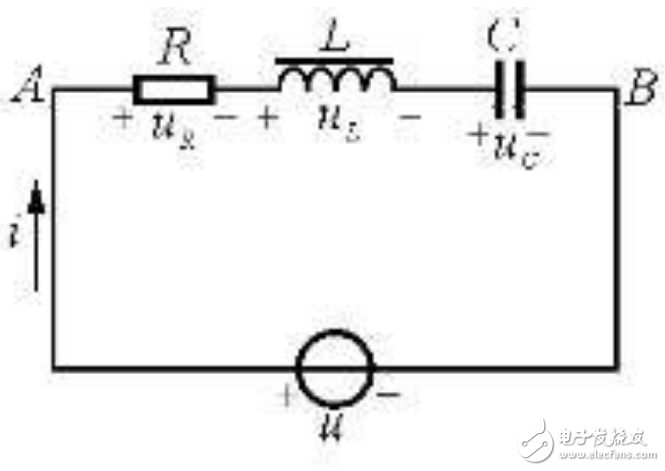
　　RLC电路：由电阻，电感，电容组成的电路。RLC电路是一种由电阻（R）、电感（L）、电容（C）组成的电路结构。RC电路是其简单的例子，它一般被称为二阶电路，因为电路中的电压或者电流的值，通常是某个由电路结构决定其参数的二阶微分方程的解。电路元件都被视为线性元件的时候，一个RLC电路可以被视作电子谐波振荡器。

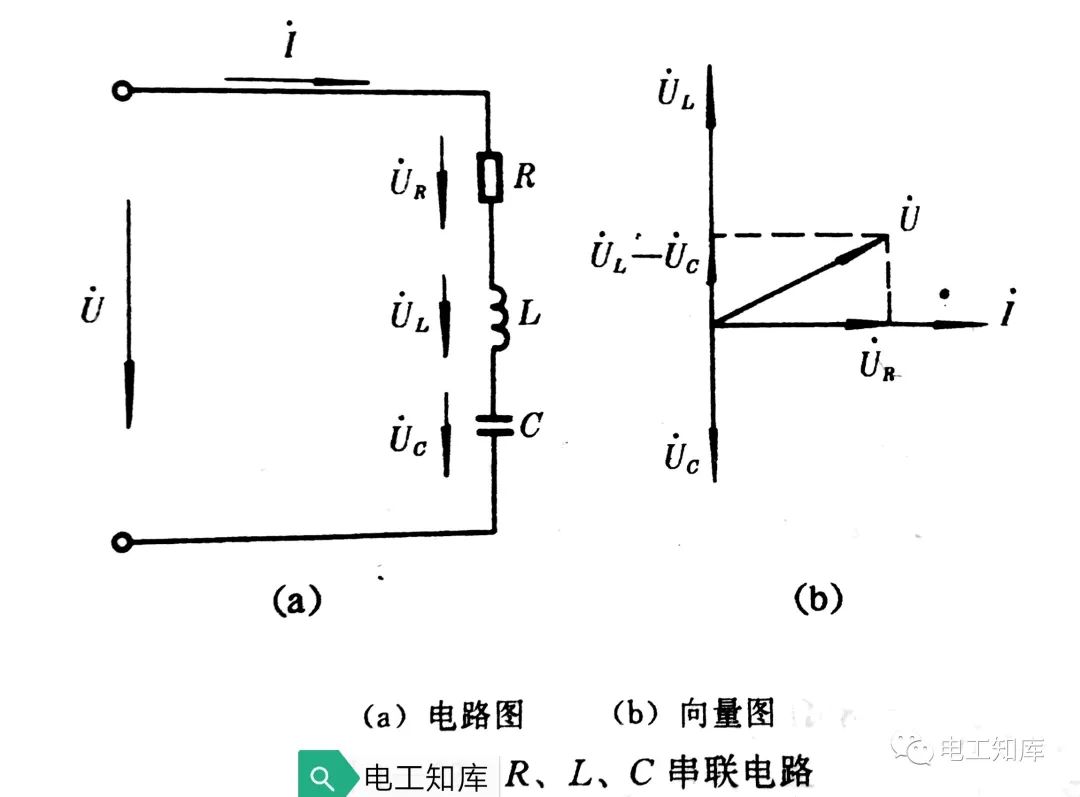
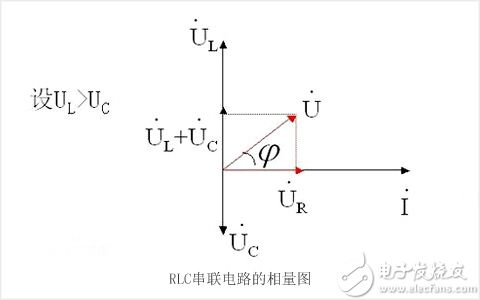
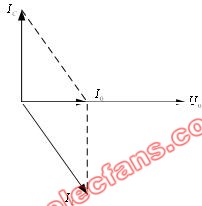
　　RLC串联电路的相量图：

　　

　　Φ=arctan（X/R）=arctan［XL-XC）/R］

　　当XL》XC时，X》0，R》0，电路呈感性

　　当XL《XC时，X《0，R》0，电路呈容性

　　当XL=XC时，X=0，R》0，电路呈电阻性 称为串联谐振状态

　　Z=［（XL-XC）^2+R^2］^（1/2） U=|z|*I

　　RLC串联谐振原理说明：

　　

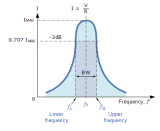
　　图示RLC串联谐振电路有选频特性：当输入端接幅度恒定的正弦交流电压源Uin时，若改变Uin的频率，输出Uout的信号幅度会随着输入信号频率的改变而改变，变化趋势如右图所示：当Uin的频率为某频率fo时Uout幅度达到最大，当Uin的频率远离fo时，Uout的输出幅度值会递减。

　　

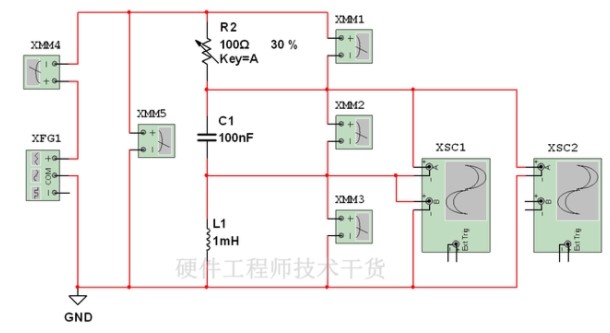
　　RLC 电路的频率响应仿真：

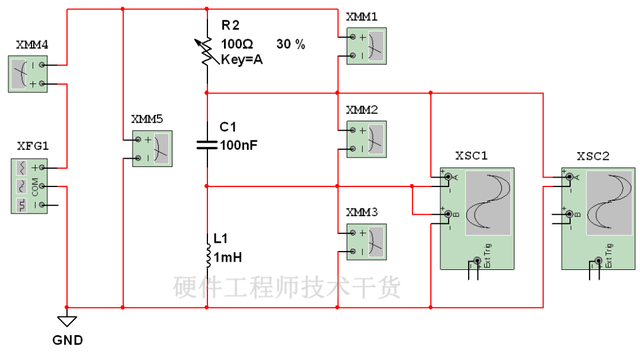
　　（1）创建仿真电路

　　在Multisim 10 仿真软件的工作界面上建立如图4所示的仿真电路， 并设置电感L1 = 25 mH， C1 = 10 nF，R1= 10Ω 。双击！ XFG1？函数发生器， 调整“Wavefrms”为正弦波， “Frequency”为1 kHz， “ Amplitude”为1 V。

　　

　　图4 RLC 串联谐振仿真电路

　　（2）打开仿真开关

　　双击！ XSC1？虚拟示波器和“ XMM1”电压表， 将电压表调整为交流档， 并拖放到合适的位置， 再调整“ XFG1”函数发生器中的“Frequency”正弦波频率， 分别观察示波器的输出电压波形和电压表的电压， 使示波器的输出电压最大或电压表输出最高; 然后记录下“XFG1”函数发生器中的“ Frequency”正弦波频率， 如图5所示。

　　

　　图5 正弦波频率

　　（3）谐振状态下的特性

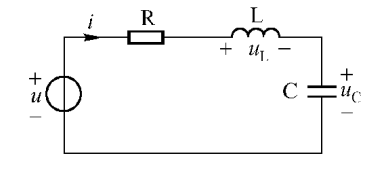
　　串联回路总电抗

　　

　　此时， 谐振回路阻抗|Z0 |为最小值， 整个回路相当于一个纯电阻电路， 激励电源的电压与回路的响应电压同相位， 如图6所示。

　　谐振时， 电感ω0L 与容抗1/ω0C相等， 电感上的电压UL 与电容上的电压UC 大小相等， 相位差180°。

　　在激励电源电压（ 有效值） 不变的情况下， 谐振回路中的电流I = Ui/ R 为最大值。

　　

　　图6 谐振时输入、输出电压的相位

　　（4）谐振电路的频率特性

　　串联回路响应电压与激励电源角频率之间的关系称为幅频特性。在Mult isim 10 仿真软件中可使用波特图仪或交流分析方法进行观察。

　　波特图仪法： 双击“ XBP1”波特图仪， 幅频特性如图7所示， 当f 0 约为10 kHz 时输出电压为最大值。

　　

　　图7 幅频特性

　　交流分析法： 选择“Simulate”菜单中的“Analy sis”进入“AC Analysis”的交流分析， 分析前进行相关设置。

　　在“Frequency Parameters”选项卡中“ Start f requency”设置为1 kHz， “Stop f requency”设置为100 kHz， 如图8所示。在“Output”选项卡中， 选择“V ［ 5］ ”为输出点， 如图9 所示。单击“Simulate”开始仿真， 交流仿真结果如图10 所示。

　　

　　图8 交流分析对话框

　　

　　图9 设置输出节点

　　

　　图10 RLC 串联幅相频特性

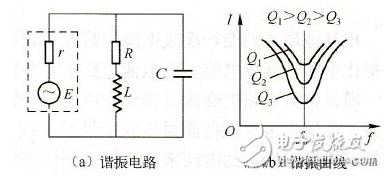
　　（5）品质因数Q

　　RLC 串联回路中的L 和C 保持不变， 改变R 的大小， 可以得出不同Q 值时的幅频特性曲线。取R =1Ω ， R = 10 和R = 100 三种阻值分别观察品质因数Q。

　　双击电阻R 1 ， 在弹出的对话框中修改电阻的阻值为1Ω ， 双击“ XBP1”波特图仪， 打开仿真开关， 幅频特性如图11 所示。

　　

　　图11 R= 1Ω 时的幅频特性

　　关闭仿真开关， 修改R1 电阻阻值为10 ， 双击“XBP1”波特图仪， 打开仿真开关， 幅频特性如图7 所示。关闭仿真开关， 将R1 电阻阻值为100 ， 双击“XBP1”波特图仪， 再打开仿真开关， 幅频特性如图12所示。

　　

　　图12 R= 100 时的幅频特性

　　显然， Q 值越高， 曲线越尖锐， 电路的选择性越好，通频带也越窄。

　　（6）结论

　　从Mult isim 10 仿真软件进行RLC 串联谐振电路实验的结果来看， RLC 串联谐振电路在发生谐振时， 电感上的电压UL 与电容上的电压UC 大小相等， 相位相反。这时电路处于纯电阻状态， 且阻抗最小， 激励电源的电压与回路的响应电压同相位。谐振频率f 0 与回路中的电感L 和电容C 有关， 与电阻R 和激励电源无关。品质因数Q 值反映了曲线的尖锐程度， 电阻R 的阻值直接影响Q 值。