品质因数(Q因数)是一个储能器件(如电感线圈、电容等)、谐振电路中所储能量同每周期损耗能量之比的一种质量指标;串联谐振回路中电抗元件的Q值等于它的电抗与其等效串联电阻的比值;元件的Q值愈大,用该元件组成的电路或网络的选择性愈佳。
Q=无功功率/有功功率
对于无辐射系统,如
Z=R+jX
则Q =|X|/RQ=无功功率/有功功率
串联谐振回路的品质因数为串联谐振回路的特性阻抗与回路电阻之比。
在串联电路中,电路的品质因数Q有两种测量方法
一是根据公式
Q=UL/U0=Uc/U0测定
Uc与UL分别为谐振时电容器C与电感线圈L上的电压;
另一种方法是通过测量谐振曲线的通频带宽度
△f=f2-f1
再根据
Q=f0/(f2-f1)
求出Q值。
式中f0为谐振频率,f2与f1是失谐时,亦即输出电压的幅度下降到最大值的
1/√2(=0.707)
倍时的上、下频率点。
Q值越大,曲线越尖锐,通频带越窄,电路的选择性越好。
在恒压源供电时,电路的品质因数、选择性与通频带只决定于电路本身的参数,与信号源无关。
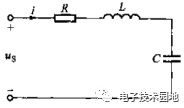
由电容C、电感L和由电容的漏电阻与电感的线电阻R所组成的串联谐振电路。
此电路的复数阻抗Z为三个元件的复数阻抗之和。
Z=R+jωL+(-j/ωC)=R+j(ωL-1/ωC)(1)
上式电阻R是复数的实部,感抗与容抗之差是复数的虚部,虚部我们称之为电抗用X表示, ω是外加信号的角频率。
当X=0时,电路处于谐振状态,此时感抗和容抗相互抵消了,即式⑴中的虚部为零,于是电路中的阻抗最小。
因此电流最大,电路此时是一个纯电阻性负载电路,电路中的电压与电流同相。
电路在谐振时容抗等于感抗,所以电容和电感上两端的电压有效值必然相等,电容上的电压有效值
UC=I*1/ωC=U/ωCR=QU
品质因数
Q=1/ωCR
这里I是电路的总电流。
电感上的电压有效值
UL=ωLI=ωL*U/R=QU
品质因数
Q=ωL/R
因为:
UC=UL
所以
Q=1/ωCR=ωL/R
电容上的电压与外加信号电压U之比
UC/U=(I*1/ωC)/RI=1/ωCR=Q
电感上的电压与外加信号电压U之比
UL/U= ωLI/RI=ωL/R=Q
从上面分析可见,电路的品质因数越高,电感或电容上的电压比外加电压越高。
电路的选择性:
电路的总电流
I=U/Z=U/[R2+(ωL-1/ωC)2]1/2=U/[R2+(ωLω0/ω0-ω0/ωCω0)2]1/2 ω0
是电路谐振时的角频率。
当电路谐振时有:
ω0L=1/ω0C所以I=U/{R2+[ω0L(ω/ω0-ω0/ω)]2}1/2= U/{R2+[R2(ω0L/R)2](ω/ω0-ω0/ω)2}1/2= U/R[1+Q2(ω/ω0-ω0/ω)2]1/2
因为电路谐振时电路的总电流
I0=U/R
所以
I=I0/[1+Q2(ω/ω0-ω0/ω)2]1/2
有:
I/I0=1/[1+Q2(ω/ω0-ω0/ω)2]1/2
作此式的函数曲线。
设(ω/ω0-ω0/ω)2=Y

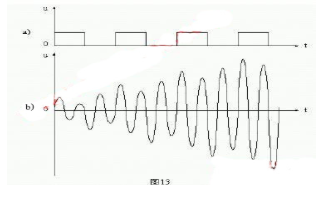
这里会有三条曲线,对应三个不同的Q值,其中有Q1》Q2》Q3。
可看出当外加信号频率ω偏离电路的谐振频率ω0时,I/I0均小于1。
Q值越高在一定的频偏下电流下降得越快,其谐振曲线越尖锐。因此也就是说电路的选择性是由电路的品质因数Q所决定的,Q值越高选择性就会越好。
 电子发烧友App
电子发烧友App









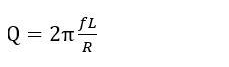












评论