为什么要计算运算放大器的闭环增益呢？有啥用

闭环增益计算

运算放大器深度负反馈状态，放大电路的增益为1/F(s)。而在实际应用中很少去计算F(s)，一般通过深度负反馈时的“虚短”、“虚断”概念去计算。深度负反馈时，1+A(s)F(s) > >1，则A(s)F(s) = Xf(s)/X’i(s)> >1，而Xi(s)=X’i(s)+Xf(s)，那么X’i(s)可以忽略不计，Xi(s)=Xf(s)。

对于深度串联负反馈，则有Ui(s)=Uf(s)；对于深度并联负反馈，则有Ii(s)=If(s)。

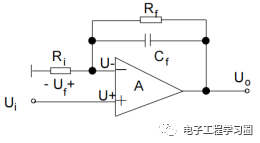
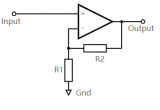
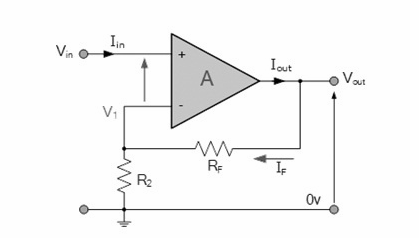
虚短、虚断示意图

如图所示，Ui加在同相输入端，同相输入端电压U+=Ui，反馈电压加在反相输入端，反相输入端电压U-=Uf，由Ui≈Uf，则U-=U+，此时，运放两个输入端之间近似短路，但又不是真正的短路，我们称为“虚短”。又因为运放的差模输入电阻Rid很大，所以当Uid=U+-U-≈0时，可以近似认为流入运放同相输入端I+和反相输入端I-电流都为0，但又不是真正的断路，我们称为“虚断”。根据这两点可以计算图中的闭环增益：

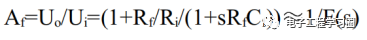
放大器电路稳定性分析

放大器的稳定性分析，都是基于闭环增益分析，如下式所示，应用于放大器的频率响应借助波特图分析。

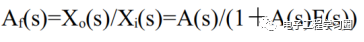
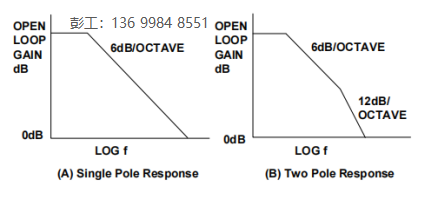
放大器对不同频率的正弦信号的稳态响应称为频率响应。放大器的频率表响应可以直接由放大器的放大倍数对频率的关系来描述，如下所示。

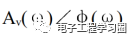
其中，Av(ω)表示电压放大倍数和频率f的关系，称为幅频响应，而Ф(ω)，表示放大器输出电压与输入电压之间的相位差和频率的关系，称为相频响应。两者综合起来可全面表征放大器的频率响应。在半对数坐标图（半对数坐标系一个轴是分度均匀的普通坐标轴，另一个轴是分度不均匀的对数坐标轴）上，一般频率采用对数分度，幅值（以db表示的电压增益）或者相角则采用线性分度。那么，这两张半对数坐标图就称为对数频率响应或波特图。

由闭环增益的算式可知，1+A(s)F(s)=0时，放大器电路会发生自激振荡，那么放大器稳定性分析就是分析1+A(s)F(s)是否等于0，那么将拉式变换转换成傅氏变换，可得自激振荡时，A(jω)F(jω)=-1。故|A(jω)F(jω)|=1，∠A(jω)F(jω)=-180°。因此，自激振荡或正反馈表现在波特图上即幅频响应图中，20lg|A(jω)|和20lg|F(jω)|曲线相交时，对应频率处的相角小于等于-180°。一般采用折线法画出电路的波特图，下面举例分析下图的波特图：

虚短、虚断示意图

由于一般情况下，Rf/Ri>>1，故F(s)≈Rf/Ri/(1+sRfCf)。然后分析幅频响应，近似画出20lg|F(jω)|的曲线，

由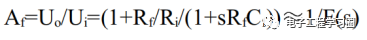

可得20lg|F(jω)|=-20lg|Rf/Ri/(1+(jωRfCf))|。那么，当ω<<1/RfCf时，20lg|F(jω)|≈-20lg|Rf/Ri|，当ω>>1/RfCf时，20lg|F(jω)|≈-20lg|Rf/Ri/(jωRfCf)|。因此，在波特图中，ω<1/RfCf时，20lg|F(jω)|是一条直线，ω>1/RfCf时，20lg|F(jω)|是一条斜线，相交点的频率为ω=1/RfCf，如下图所示：

波特图

同理ω<<1/RfCf时，∠F(jω)=∠Rf/Ri=0°，当ω>>1/RfCf时，∠F(jω)=∠Rf/Ri/(jωRfCf)=-90°，当ω=1/RfCf时，∠F(jω)=-45°。分析放大器稳定，主要是检查∠A(jω)F(jω)，还需要开环增益的幅频曲线，一般从器件资料中查看。现举例分析图中曲线，上图中粗黑线表示20lg|F(jω)|，相频特性是根据20lg|A(jω)F(jω)| = 20lg|A(jω)|-20lg1/|F(jω)|得到。

可以看到20lg|A(jω)|和20lg1/|F(jω)|曲线相交时，对应相角大约是-100°大于-180°电路稳定。我们可以看到，在fc之前，相角达到了-135°，若20lg1/|F(jω)|曲线拐点再往高频移动一些，fc或fc之前对应的相角就有可能达到-180°，从而使电路处于不稳定状态。

审核编辑：刘清