k means聚类算法实例

所谓聚类问题，就是给定一个元素集合D，其中每个元素具有n个可观察属性，使用某种算法将D划分成k个子集，要求每个子集内部的元素之间相异度尽可能低，而不同子集的元素相异度尽可能高。其中每个子集叫做一个簇。

与分类不同，分类是示例式学习，要求分类前明确各个类别，并断言每个元素映射到一个类别，而聚类是观察式学习，在聚类前可以不知道类别甚至不给定类别数量，是无监督学习的一种。目前聚类广泛应用于统计学、生物学、数据库技术和市场营销等领域，相应的算法也非常的多。

K-Means算法实例

例：以下是一组用户的年龄数据，将K值定义为2对用户进行聚类。并随机选择16和22作为两个类别的初始质心。

Data_Age = ［15，15， 16， 19， 19， 20， 20， 21， 22， 28， 35， 40， 41， 42， 43， 44， 60， 61， 65］;

CenterId1 =16， CenterId2 = 22

（1）、计算距离并划分数据

通过计算所有用户的年龄值与初始质心的距离对用户进行第一次分类。计算距离的方法是使用欧式距离。距离值越小表示两个用户间年龄的相似度越高。

第一次迭代：

Data_Age = ［15，15， 16， 19， 19， 20， 20， 21， 22， 28， 35， 40， 41， 42， 43， 44， 60， 61， 65］;

Distance（16）= ［1， 1， 0， 3， 3， 4， 4， 5， 6， 12， 19， 24， 25， 26， 27， 28，44， 45， 49］;

Distance（22）= ［7， 7，6， 3， 3， 2， 2， 1， 0， 6， 13， 18， 19， 20， 21， 22， 38， 39，43］;

Group1_（16）= ［15，15， 16］; Mean =15.33

Group2_（22）= ［19，19， 20， 20， 21， 22， 28， 35， 40， 41， 42， 43， 44， 60， 61， 65］; Mean = 36.25

（2）、使用均值作为新的质心

将两个分组中数据的均值作为新的质心，并重复之前的方法，迭代计算每个数据点到新质心的距离，将数据点划分到与之距离较小的类别中。

第二次迭代：

Data_Age = ［15，15， 15.33， 16， 19， 19， 20， 20， 21， 22， 28，35， 36.25， 40， 41， 42， 43， 44， 60， 61， 65］;

Distance（15.33）=［0.33， 0.33， 0.67，3.67， 3.67， 4.67， 4.67， 5.67， 6.67， 12.67， 19.67， 24.67， 25.67， 26.67，27.67， 28.67， 44.67， 45.67， 49.67］;

Distance（36.25）=［21.25， 21.25， 20.25， 17.25， 17.25， 16.25，16.25， 15.25， 14.25， 8.25， 1.25， 3.75， 4.75， 5.75，6.75， 7.75， 23.75， 24.75， 28.75］;

Group1_（15.33）=［ 15， 15， 16， 19， 19， 20， 20， 21， 22］; Mean = 18.56

Group2_（36.25）=［ 28， 35， 40， 41， 42， 43， 44， 60， 61，65］; Mean = 45.90

第三次迭代：

Data_Age = ［15，15， 16， 18.56， 19， 19， 20， 20， 21， 22， 28，35， 40， 41， 42， 43， 44， 45.90， 60， 61， 65］;

Distance（18.56）=［3.56， 3.56， 2.56，0.44， 0.44， 1.44， 1.44， 2.44， 3.44， 9.44， 16.44， 21.44， 22.44， 23.44，24.44， 25.44， 41.44， 42.44， 46.44］;

Distance（45.90）=［30.90， 30.90， 29.90， 26.90， 26.90， 25.90，25.90， 24.90， 23.90， 17.90， 10.90， 5.90， 4.90， 3.90，2.90， 1.90， 14.10， 15.10， 19.10］;

Group1_（18.56）=［ 15， 15， 16， 19， 19， 20， 20， 21， 22， 28］; Mean = 19.50

Group2_（45.90）=［ 35， 40， 41， 42， 43， 44， 60， 61， 65］; Mean = 47.89

第四次迭代：

Data_Age = ［15，15， 16， 19， 19， 19.50， 20， 20， 21， 22， 28，35， 40， 41， 42， 43， 44， 47.89， 60， 61， 65］;

Distance（19.50）=［4.5， 4.5， 3.5，0.5， 0.5， 0.5， 0.5， 1.5， 2.5， 8.5， 15.5， 20.5， 21.5， 22.5， 23.5， 24.5，40.5， 41.5， 45.5］;

Distance（47.89）=［32.89， 32.89， 31.89， 28.89， 28.89， 27.89，27.89， 26.89， 25.89， 19.89， 12.89， 7.89， 6.89， 5.89，4.89， 3.89， 12.11， 13.11， 17.11］;

Group1_（19.50）=［ 15， 15， 16， 19， 19， 20， 20， 21， 22，28］; Mean = 19.50

Group2_（47.89）=［ 35， 40， 41， 42， 43， 44， 60， 61， 65］; Mean = 47.89

（3）、算法停止条件

迭代计算每个数据到新质心的距离，直到新的质心和原质心相等，算法结束。

MATLAB中的kmeans函数

MATLAB中的kmeans函数采用的是将N*P的矩阵X划分为K个类，使得类内对象之间的距离最大，而类之间的距离最小。

使用方法：

Idx = Kmeans（X，K）

［Idx， C］ = Kmeans（X，K）

［Idc， C， sumD］ = Kmeans（X，K）

［Idx， C， sumD， D］ = Kmeans（X，K）

各输入输出参数介绍：

X---N*P的数据矩阵

K---表示将X划分为几类，为整数

Idx---N*1的向量，存储的是每个点的聚类标号

C---K*P的矩阵，存储的是K个聚类质心位置

sumD---1*K的和向量，存储的是类间所有点与该类质心点距离之和

D---N*K的矩阵，存储的是每个点与所有质心的距离

［┈］ = Kmeans（┈，’Param1’，’Val1’，’Param2’，’Val2’，┈）

其中参数Param1、Param2等，主要可以设置为如下：

1、’Distance’---距离测度

‘sqEuclidean’---欧氏距离

‘cityblock’---绝对误差和，又称L1

‘cosine’---针对向量

‘correlation’---针对有时序关系的值

‘Hamming’---只针对二进制数据

2、’Start’---初始质心位置选择方法

‘sample’---从X中随机选取K个质心点

‘uniform’---根据X的分布范围均匀的随机生成K个质心

‘cluster’---初始聚类阶段随机选取10%的X的子样本（此方法初始使用’sample’方法）

Matrix提供一K*P的矩阵，作为初始质心位置集合

3、’Replicates’---聚类重复次数，为整数

MATLAB代码：

% KMeans算法的基本思想是初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。

% 然后按平均法重新计算各个簇的质心，从而确定新的簇心。一直迭代，直到簇心的移动距离小于某个给定的值。

% 随机获取200个点

X = ［randn（50，2）+［-ones（50，1）， +ones（50，1）］; randn（50，2）+［ones（50，1）， ones（50，1）］; 。。。

randn（50，2）+［ones（50，1）， -ones（50，1）］; randn（50，2）+［-ones（50，1），-ones（50，1）］］;

%{

MATLAB中的kmeans函数采用的是将N*P的矩阵X划分为K个类，使得类内对象之间的距离最大，而类之间的距离最小。

使用方法：

Idx = Kmeans（X，K）

［Idx，C］ = Kmeans（X，K）

［Idc，C，sumD］ = Kmeans（X，K）

［Idx，C，sumD，D］ = Kmeans（X，K）

各输入输出参数介绍：

X---N*P的数据矩阵

K---表示将X划分为几类，为整数

Idx---N*1的向量，存储的是每个点的聚类标号

Ctrs---K*P的矩阵，存储的是K个聚类质心位置

sumD---1*K的和向量，存储的是类间所有点与该类质心点距离之和

D---N*K的矩阵，存储的是每个点与所有质心的距离

%}

opts = statset（‘Display’，‘final’）;

［Idx，Ctrs，SumD，D］ = kmeans（X，4，‘Replicates’，4，‘Options’，opts）;

% 画出聚类为1的点。

% X（Idx==1，1），为第一类的样本的第一个坐标；X（Idx==1，2）为第一类的样本的第二个坐标

plot（X（Idx==1，1）， X（Idx==1，2）， ‘r.’， ‘MarkerSize’， 14）;

hold on;

plot（X（Idx==2，1）， X（Idx==2，2）， ‘b.’， ‘MarkerSize’， 14）;

hold on;

plot（X（Idx==3，1）， X（Idx==3，2）， ‘g.’， ‘MarkerSize’， 14）;

hold on;

plot（X（Idx==4，1）， X（Idx==4，2）， ‘y.’， ‘MarkerSize’， 14）;

hold on;

% 绘出聚类中心点，kx表示是交叉符

plot（Ctrs（：，1）， Ctrs（：，2）， ‘kx’， ‘MarkerSize’， 14， ‘LineWidth’， 4）;

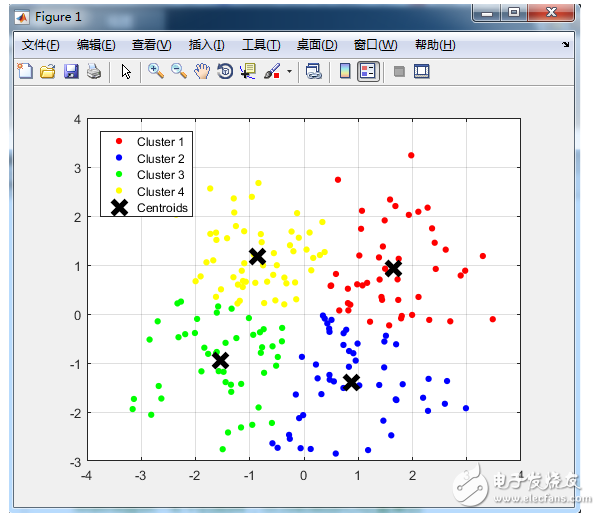
legend（‘Cluster 1’， ‘Cluster 2’， ‘Cluster 3’， ‘Cluster 4’， ‘Centroids’， ‘Location’， ‘NW’）;

grid on;

%{

［┈］ = Kmeans（┈，’Param1’，’Val1’，’Param2’，’Val2’，┈）

其中参数Param1、Param2等，主要可以设置为如下：

1、‘Distance’---距离测度

‘sqEuclidean’---欧氏距离

‘cityblock’---绝对误差和，又称L1

‘cosine’---针对向量

‘correlation’---针对有时序关系的值

‘Hamming’---只针对二进制数据

2、‘Start’---初始质心位置选择方法

‘sample’---从X中随机选取K个质心点

‘uniform’---根据X的分布范围均匀的随机生成K个质心

‘cluster’---初始聚类阶段随机选取10%的X的子样本（此方法初始使用’sample’方法）

Matrix提供一K*P的矩阵，作为初始质心位置集合

3、‘Replicates’---聚类重复次数，为整数

%}