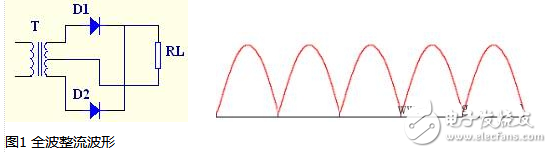
全波整流电路图(一)
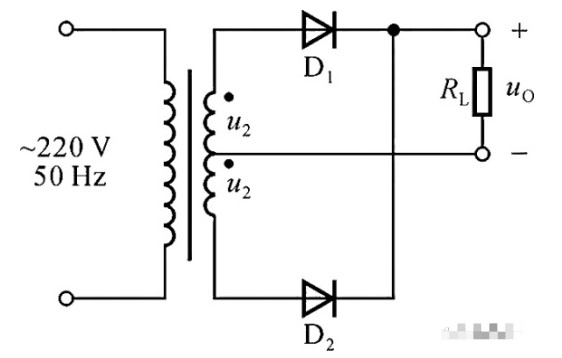
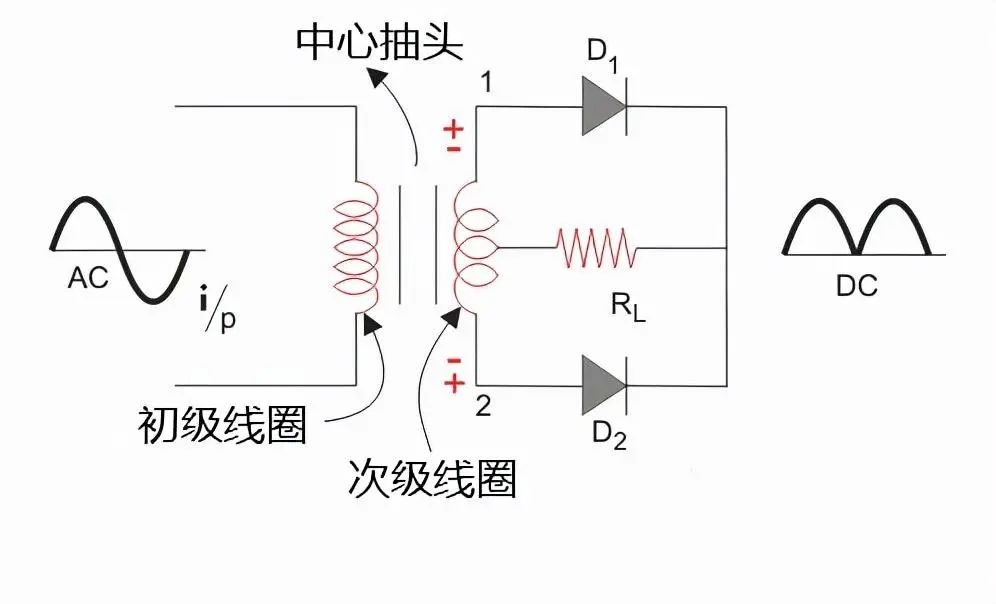
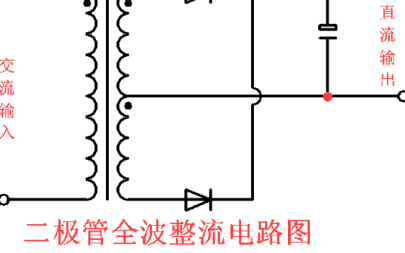
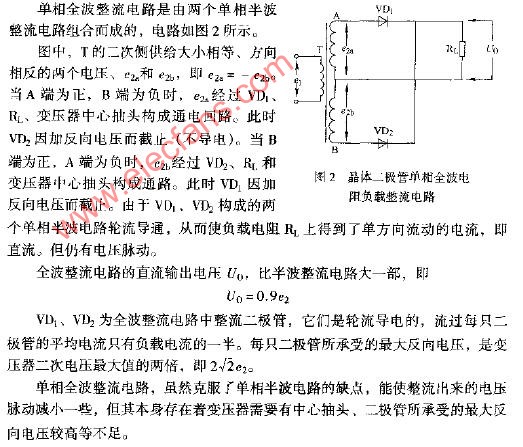
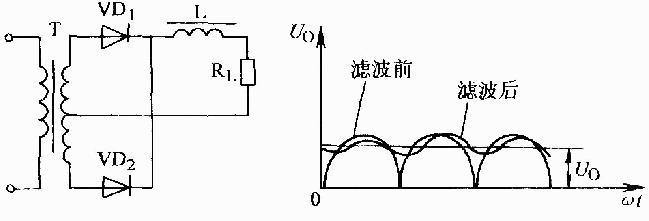
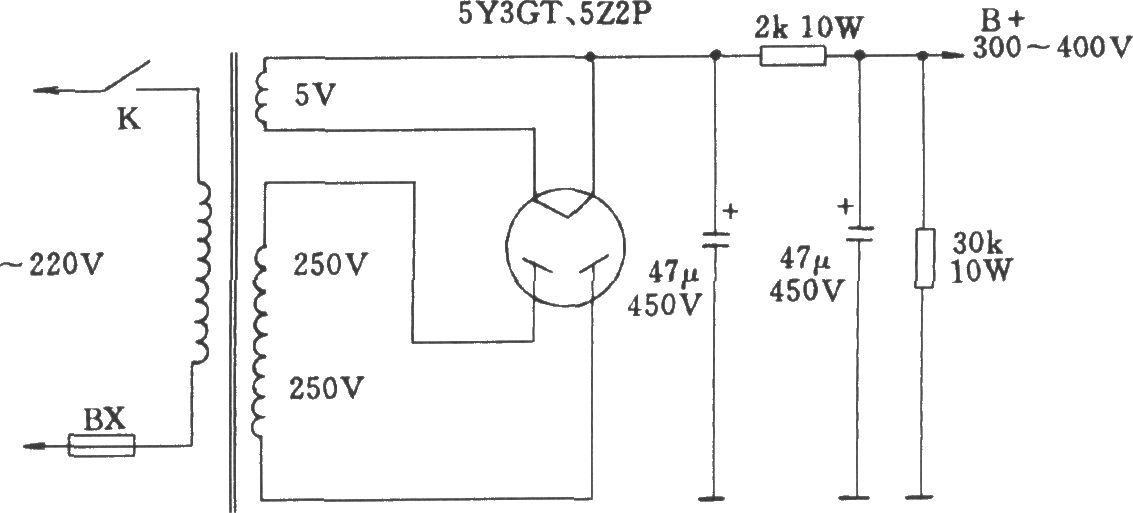
如图所示,全波整流电路只需二只整流二极管,但电源变压器却需要有带中心抽头的两组相同电压的绕组。利用带中心抽头的变压器,使它们在交流电的正半周和负半周分别向RL供给同一方向的电流,从而构成全波整流电路。
设交流电在正半周时,变压器输出电压极性为上正下负,上半绕组电源经D1、R、中心抽头形成回路,而下半绕组不通,此时D1导通D2不导通,电流ID1经RL成回路;在负半周时,电压极性与前相反,可知D2导通而D1不导通,ID2以相同方向经RL成回路,由此在负载上得到的是正负两个半周都有整流输出的波形,故称为全波整流。这时经整流的直流(平均值)电压为半波整流的两倍,而且脉动情况也有一定的改善,这种整流电路的缺点是每组线圈只有一半的时间通过电流,所以变压器的利用率不高。
全波整流电路图(二)
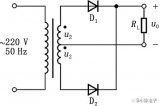
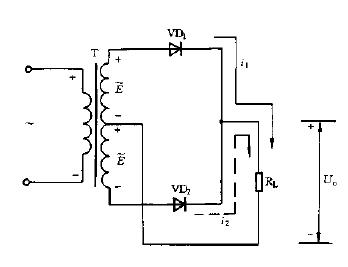
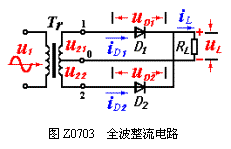
全波整流电路如图Z0703所示。它是由次级具有中心抽头的电源变压器Tr、两个整流二极管D1、D2和负载电阻RL组成。变压器次级电压u21和u22大小相等,相位相反,即
u21=-u22=
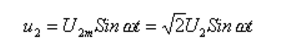
式中,U2是变压器次级半边绕组交流电压的有效值。
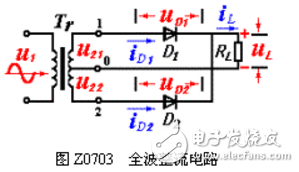
全波整流电路的工作过程是:在u2的正半周(ωt=0~π)D1正偏导通,D2反偏截止,RL上有自上而下的电流流过,RL上的电压与u21相同。
在u2的负半周(ωt=π~2π),D1反偏截止,D2正偏导通,RL上也有自上而下的电流流过,
RL上的电压与u22相同。可画出整流波形如图Z0704所示。可见,负载凡上得到的也是一单向脉动电流和脉动电压。其平均值分别为:

加在二极管两端的最高反向电压为
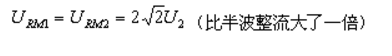
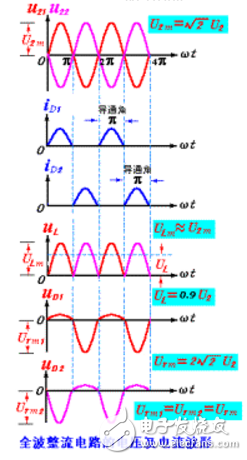
选择整流二极管时,应以此二参数为极限参数。
全波整流输出电压的直流成分(较半波)增大,脉动程度减小,但变压器需要中心抽头、制造麻烦,整流二极管需承受的反向电压高,故一般适用于要求输出电压不太高的场合。
全波整流电路图(三)
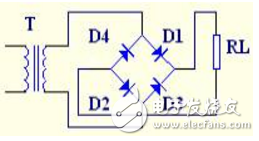
图1
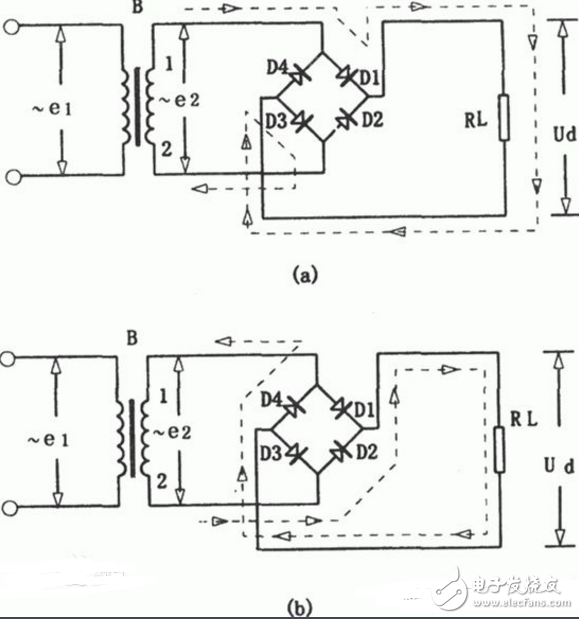
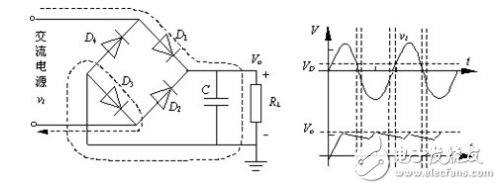
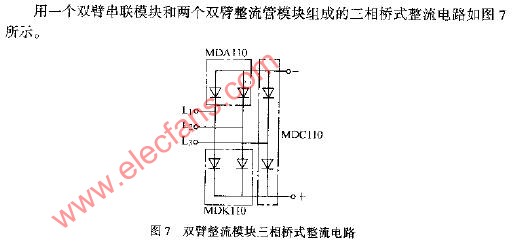
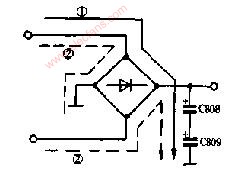
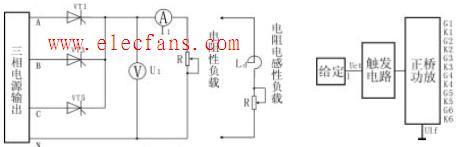
桥式整流电路,也可认为它是全波整流电路的一种,变压器绕组按图1方法接四只二极管。D1~D4为四只相同的整流二极管,接成电桥形式,故称桥式整流电路。利用二极管的导引作用,使在负半周时也能把次级输出引向负载。具体接法如图所示,从图中可以看到,在正半周时由D1、D2导引电流自上而下通过RL,负半周时由D3、D4导引电流也是自上而下通过RL,从而实现了全波整流。在这种结构中,若输出同样的直流电压,变压器次级绕组与全波整流相比则只须一半绕组即可,但若要输出同样大小的电流,则绕组的线径要相应加粗。至于脉动,和前面讲的全波整流电路完全相同。
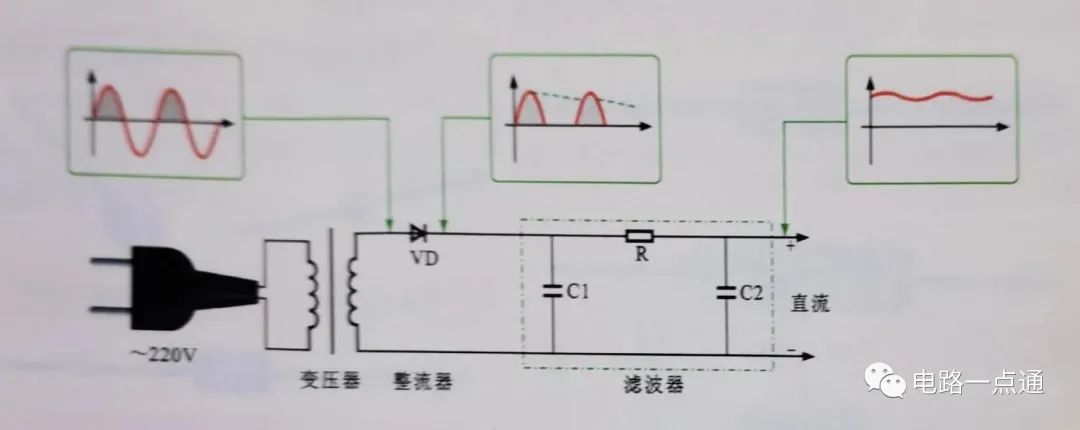
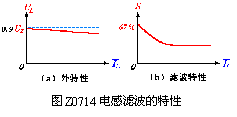
由于整流电路的输出电压都含有较大的脉动成分。为了尽量压低脉动成分,另一方面还要尽量保留直流成分,使输出电压接近理想的直流,这种措施就是滤波。滤波通常是利用电容或电感的能量存储作用来实现的。
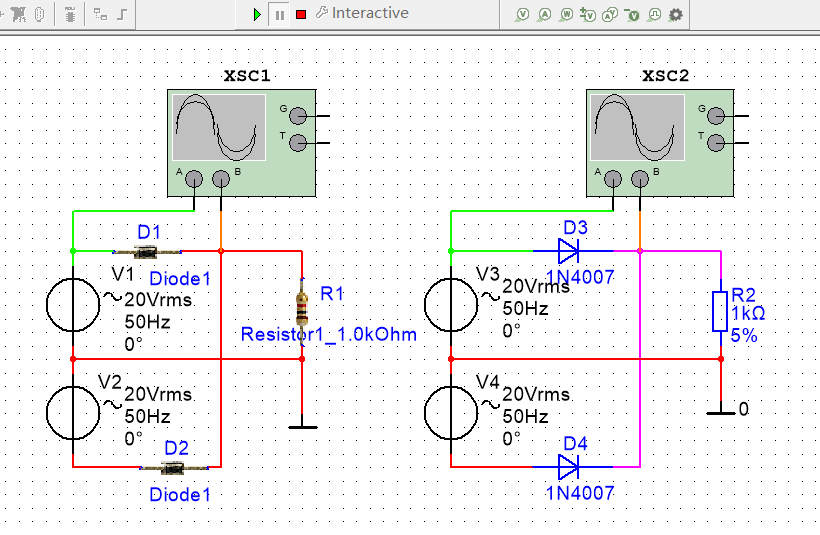
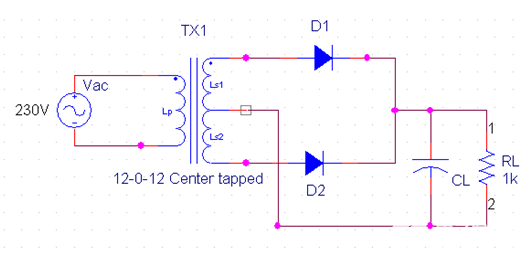
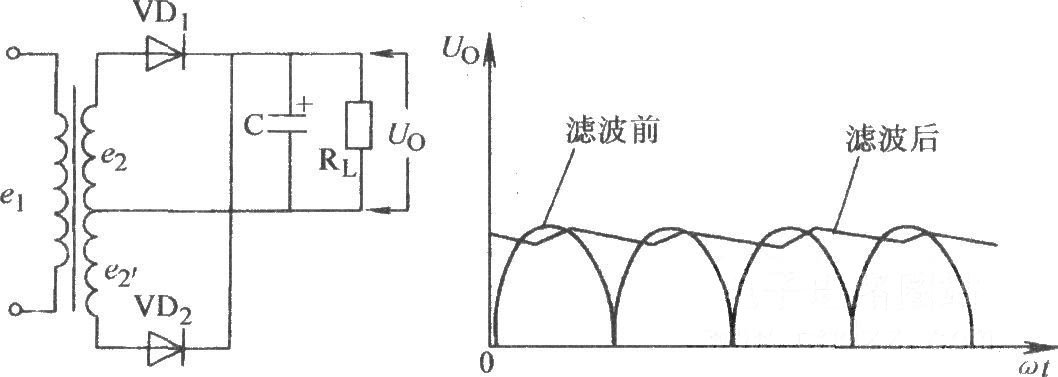
在本实验电路中采用的是电容滤波,即在负载电阻RL上并联一个滤波电容C,电路如图2,滤波后的波形如下图。
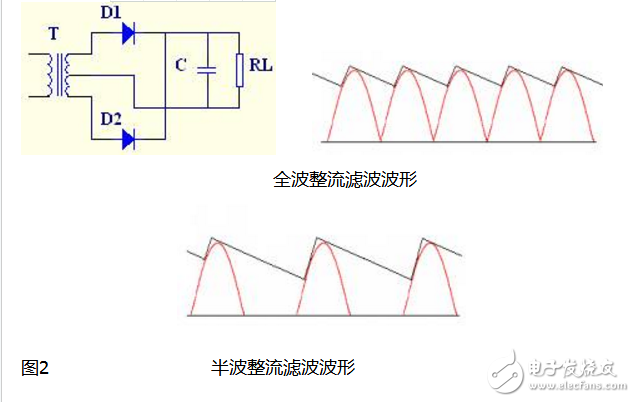
全波整流电路图(四)
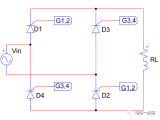
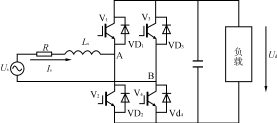
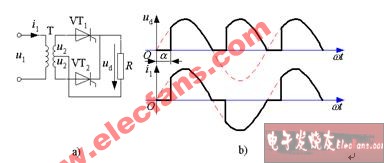
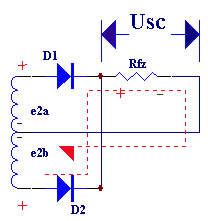
当输入电压处于交流电压的正半周时,二极管D1导通,输出电压Vo=vi-VD1。当输入电压处于交流电压的负半周时,二极管D2导通,输出电压Vo=vi-VD2。
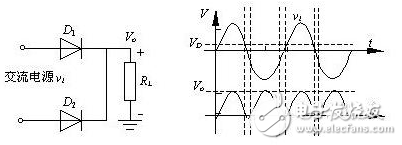
由上述分析可知,二极管全波整流电路输出的仍然是一个方向不变的脉动电压,但脉动频率是半波整流的一倍。
全波整流电路图(五)
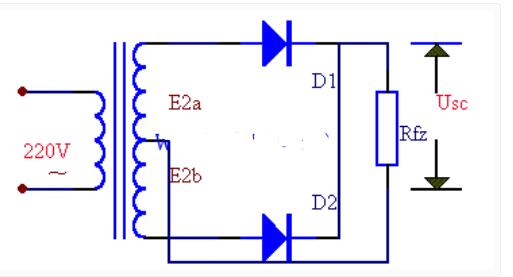
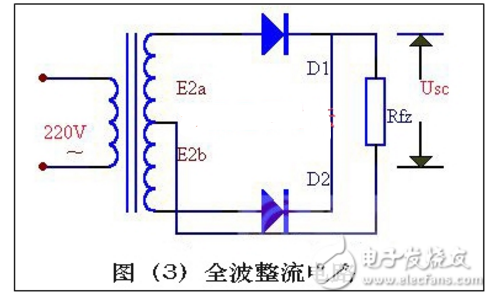
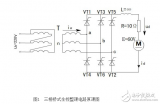
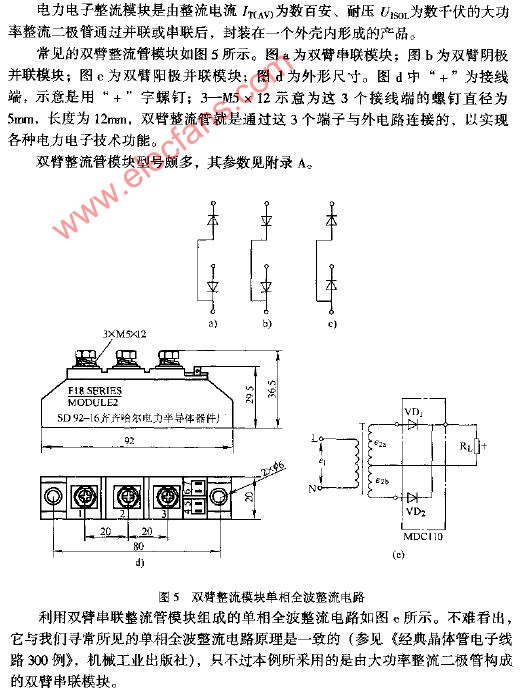
如果把整流电路的结构作一些调整,可以得到一种能充分利用电能的全波整流电路。图5-3是全波整流电路的电原理图。
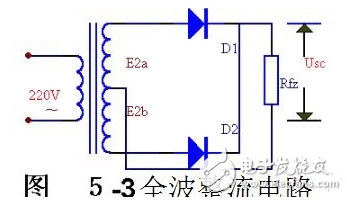
全波整流电路,可以看作是由两个半波整流电路组合成的。变压器次级线圈中间需要引出一个抽头,把次组线圈分成两个对称的绕组,从而引出大小相等但极性相反的两个电压e2a、e2b,构成e2a、D1、Rfz与e2b、D2、Rfz,两个通电回路。
全波整流电路的工作原理,可用图5-4所示的波形图说明。在0~π间内,e2a对Dl为正向电压,D1导通,在Rfz
上得到上正下负的电压;e2b对D2为反向电压,D2不导通(见图5-4(b)。在π-2π时间内,e2b对D2为正向电压,D2导通,在Rfz
上得到的仍然是上正下负的电压;e2a对D1为反向电压,D1不导通(见图5-4(C)。
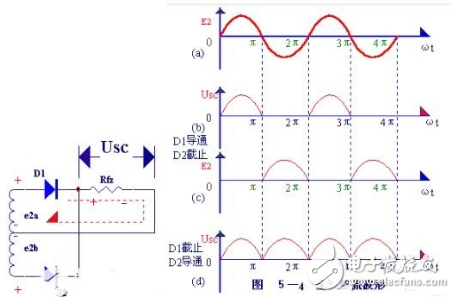
如此反复,由于两个整流元件D1、D2轮流导电,结果负载电阻Rfz
上在正、负两个半周作用期间,都有同一方向的电流通过,如图5-4(b)所示的那样,因此称为全波整流,全波整流不仅利用了正半周,而且还巧妙地利用了负半周,从而大大地提高了整流效率(Usc=0.9e2,比半波整流时大一倍)。
图5-3所示的全波整滤电路,需要变压器有一个使两端对称的次级中心抽头,这给制作上带来很多的麻烦。另外,这种电路中,每只整流二极管承受的最大反向电压,是变压器次级电压最大值的两倍,因此需用能承受较高电压的二极管。
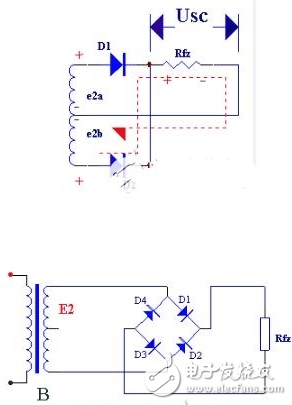
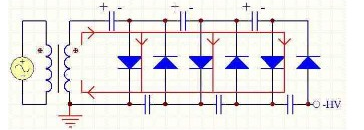
图5-5(a)为桥式整流电路图,(b)图为其简化画法。
全波整流电路图(六)
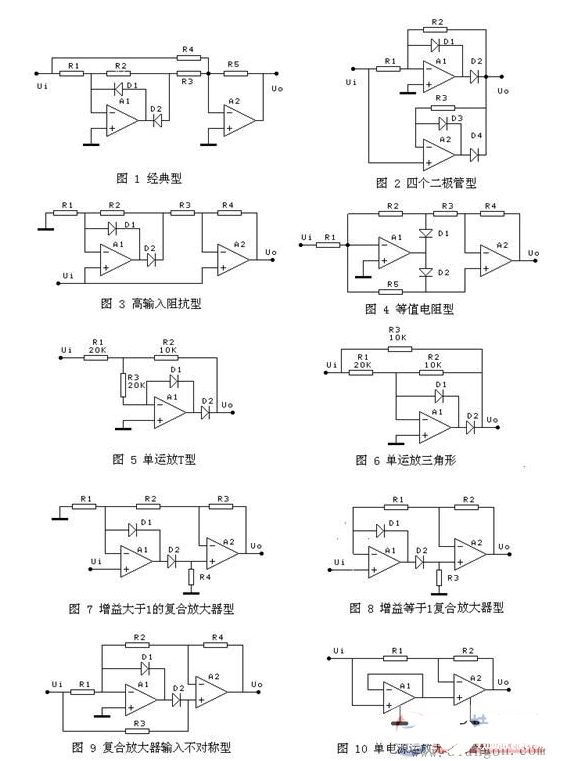
利用二极管(开关器件)的单向导电特性,和放大器的优良放大性能相结合,可做到对输入交变信号(尤其是小幅度的电压信号)进行精密的整流,由此构成精密半波整流电路。若由此再添加简单电路,即可构成精密全波整流电路。
二极管的导通压降约为0.6V左右,此导通压降又称为二极管门坎电压,意谓着迈过0.6V这个坎,二极管才由断态进入到通态。常规整流电路中,因整流电压的幅值远远高于二极管的导通压降,几乎可以无视此门坎电压的存在。但在对小幅度交变信号的处理中,若信号幅度竟然小于0.6V,此时二极管纵然有一身整流的本事,也全然派不上用场了。
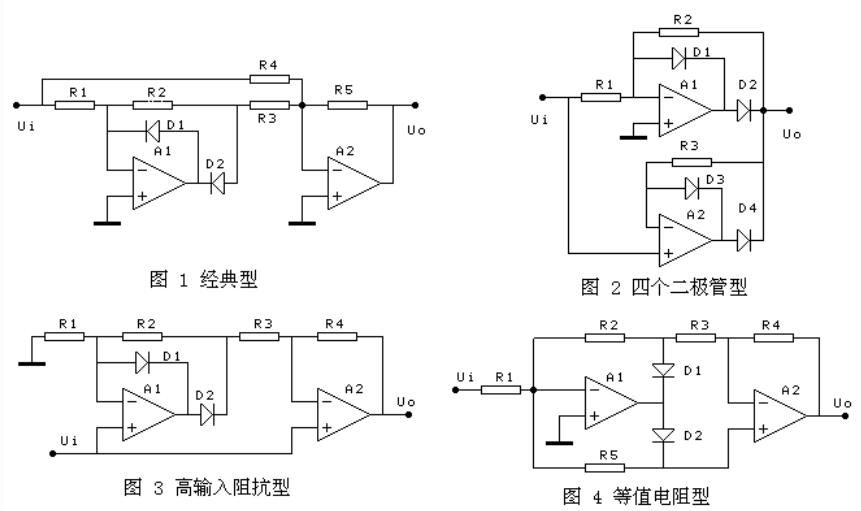
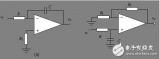
在二极管茫然四顾之际,它的帮手——有优良放大性能的运算放大器的适时出现,改变了这种结局,二者一拍即合,小信号精密半波整流电路即将高调登场。请看图1。
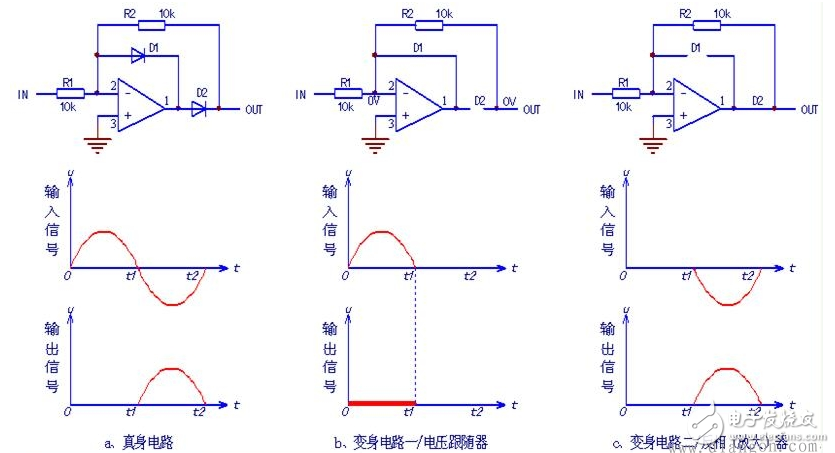
图1 半波精密整流电路及等效电路
上图电路,对输入信号的正半波不予理睬,仅对输入信号的负半波进行整流,并倒相后输出。
(1)在输入信号正半周(0~t1时刻),D1导通,D2关断,电路等效为电压跟随器(图中b电路):
在D1、D2导通之前,电路处于电压放大倍数极大的开环状态,此时(输入信号的正半波输入期间),微小的输入信号即使放大器输入端变负,二极管D1正偏导通(相当于短接),D2反偏截止(相当于断路),形成电压跟随器模式,因同相端接地,电路变身为跟随地电平的电压跟随器,输出端仍能保持零电位。
(2)在输入信号负半周(t1~t2时刻),D1关断,D2导通,电路等效反相器(图中c电路):
在输入信号的负半波期间,(D1、D2导通之前)微小的输入信号即使输出端变正,二极管D1反偏截止,D2正偏导通,形成反相(放大)器的电路模式,对负半波信号进行了倒相输出。
在工作过程中,两只二极管默契配合,一开一关,将输入正半波信号关于门外,维持原输出状态不变;对输入负半波信号则放进门来,帮助其翻了一个跟头(反相)后再送出门去。两只二极管的精诚协作,再加上运算放大器的优良放大性能,配料充足,做工地道,从而做成了精密半波整流这道“大餐”。
如果调整反馈电阻R2的阻值,使R2=2R1,再与输入信号相混合,则形成全波精密整流电路,如图2所示。
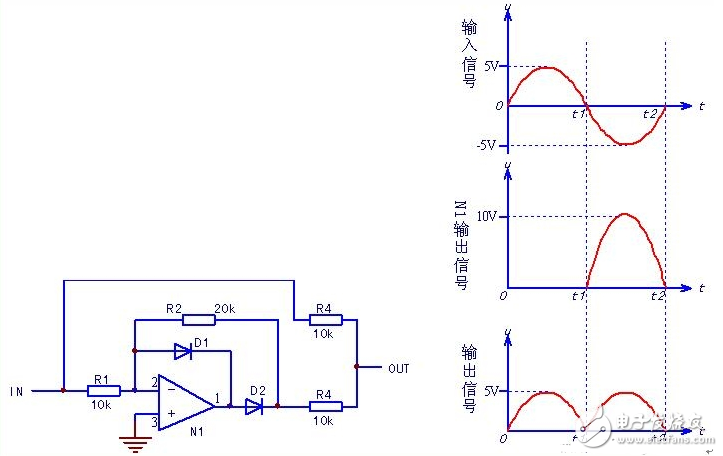
图2 精密全波整流电路及波形图
将N1放大器的反馈电阻R2增大,使R2=2R1,使其将整流信号反相放大两倍后输出,再与输入信号相加,其整流的+10V与输入负半波的-5V相加,10+(-5)=5,恰好能将负半波“消灭”掉,得到全波整流电压。
所谓魔电(模电),如果能够识破其变身术,只剩下一个个的电路模型,又何魔之有?
对精密整电路的故障检测,其前提是:所有运算放大器,均是直流放大器,甚至可以施加直流电压信号来确定电路好坏。
(1)输入信号电压为零时,输出端(D2的负端为输出端),输出电压也为0V;
(2)正的电压信号输入时,输出端保持0V;
(3)负的电压信号输入时,IN=-OUT
常见全波精密整流电路形式:
(1)精密全波整流电路之一

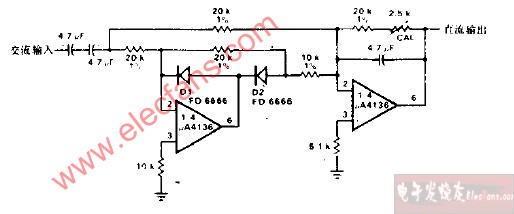
图3 精密全波整流电路之一
如图3中的a电路所示,N1及外围电路构成正半波输入2倍压反相整流放大电路,N2为反相求和电路。若输入信号峰值为±2V的正弦波信号电压,则a点输出为-4V对应输入正半波的电压信号;此信号经在N1反相输入端与输入信号相加(-4V+2V=-2V),得到-2V的脉动直流(在后级电路需要正的采样电压时)输入信号,又经N2反相求和电路,得到2V脉动直流信号。电路起到全波或桥式整流电路同样的作用,但整流线性和精度得到保障。
该电路形式比之图3电路,采用一级反相加法器,为实用电路。另外,若令R1=R2=R4=R5,令R3=1/2R1,将偏置电路的参数改变后,电路全波整流性能仍然是相同的。同一功能电路,可以有多种设计模式,正所谓条条大道通罗马。
(2)精密全波整流电路之二
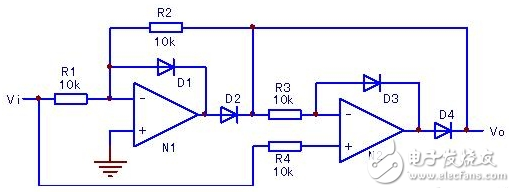
图4 精密全波整流电路之二
将图4全波整流电路的工作原理简述如下:输入正半波期间(Vi》0),N1输入端电压《0,D1通,D2断;同时正向输入电压送入N2同相输入端,D3、D4通。此时等效为电压跟随器电路,将正半波信号输送到Vo端,即Vi=Vo。
在输入负半波期间(Vi《0),N1的输出端》0,D1断,D2通;N2因输入负半波导致D4断,D3通,输出信号回路被阻断。此时N1变身为反相器电路,将输入负半波倒相后送至Vo端。
利用D1~D2的单向导电——通、断特性与放大器配合,巧妙地完成了全波整流任务。
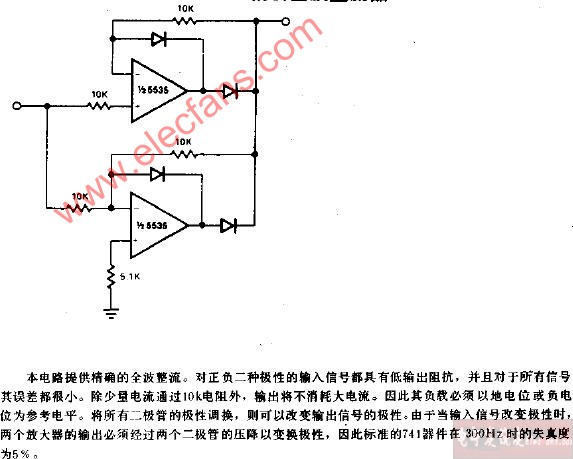
(3)精密全波整流电路之三
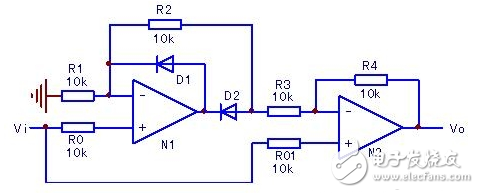
图5 精密全波整流电路之三
将图5电路简述一下:此为高输入阻抗(输入信号进入N1、N2的同相输入端,输入信号电流近于零)全波整流电路,输入正半波期间,D1通,D2断,N2(此时为电压跟随器)将输入正半波送至Vo端;输入负半波期间,D1断,D2通,N1此时变身为2倍压同相放大器,其输出信号电压向Vi信号同时送入N2(此时变身为减法器),经相减后输出负向的全波整流电压。
分析该电路原理(如图5),除了采用电阻串联分压那把金钥匙之处,尚应注意以下两点:
1)确定电路的基本电路构成。如N1为2倍压反相放大器,N2为减法器电路;
2)动态中“变身倾向”的定性。如N2在输入正半波期间变身为电压跟随器。
掌握此两个要点,根据信号输入(动、静态或正、负半波状态)变化,把握放大器的“七十二变”,从而推导出输出端信号电压的变化规律。
对精密整电路的故障检测,前文已有述及,可更为简化为一个原则:输出为输入的绝对值。要么Vi=Vo,要么Vi=-Vo。此为检测其工作状态的依据。
 电子发烧友App
电子发烧友App











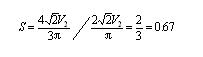










评论