所谓传递函数即线性定常系统在零初始条件下,输出量的拉氏变换式与输入量的拉氏变换式之比。传递函数通常用于单输入、单输出的模拟电路,主要用在信号处理、通信理论、控制理论。这个术语经常专门用于如本文所述的线性时不变系统(LTI)。实际系统基本都有非线性的输入输出特性,但是许多系统在标称参数范围内的运行状态非常接近于线性,所以实际应用中完全可以应用线性时不变系统理论表示其输入输出行为,有的书中也把其译为:“转移函数”。
n阶滤波器传递函数的一般表达式为
![]()
若将传递函数分解为因子式,则上式变为
![]()
式中,sao?,sa1,…,sas咖为传递函数的极点;sbo,sb1执,…,sbm为传递函数的零点。
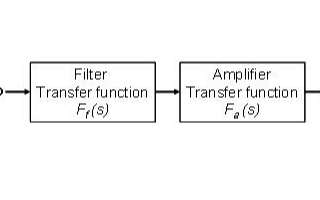
在设计滤波器的电路时,直接实现3阶以上传递函数的电路是很难的。当需要设计大于或即是3阶的滤波器时,一般采取将高阶传递函数分解为几个低阶传递函数乘积的形式。如
Gn(s)=G1(S).G2(S)… Gk(s)
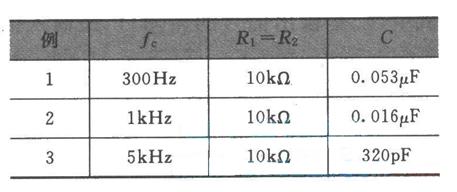
式中,k≤n。例如,设计一个5阶滤波器,可用两个2阶滤波器和一个1阶滤波器级联得到。

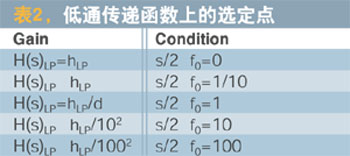
表中,G(s)为滤波器的传递函数,c(ω)为滤波器的幅频特性,G0为滤波器的通带增益或零频增益,ωc为一阶滤波器的截止角频率,ωn为二阶滤波器的自然角频率,ω0为带通或带阻滤波器的中心频率,ε为2阶滤波器的阻尼系数。
将k个低阶传递函数的滤波器的基本节级联起来,可构成n阶滤波器。由于用集成运放构成的低阶滤波器,其输出阻抗很低9所以不必考虑各基本节级联时的负载效应,保证了各基本节传递函数设计的独立性。
一阶滤波器和二阶滤波器是设计集成有源滤波器的基础,表列出了常用的一阶、二阶滤波器的传递函数和幅频特性。在设计滤波器时,可直接查表得到其传递函数,这样就避免了在设计滤波器时求解传递函数的麻烦。
二阶低通滤波器

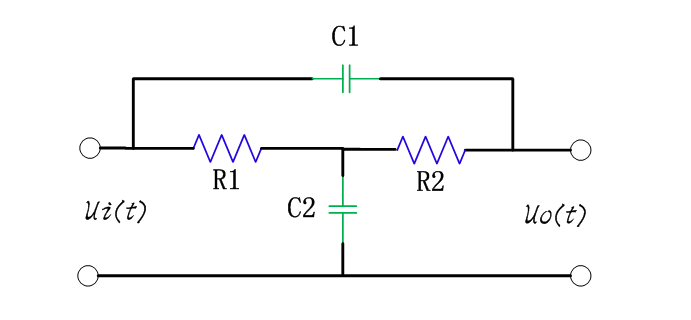
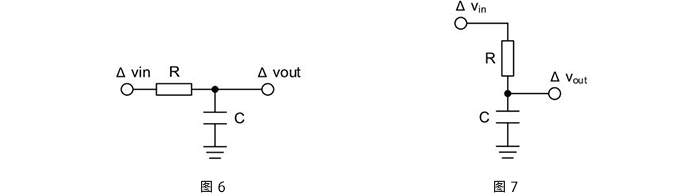
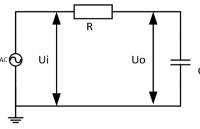
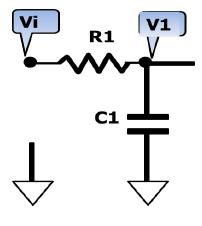
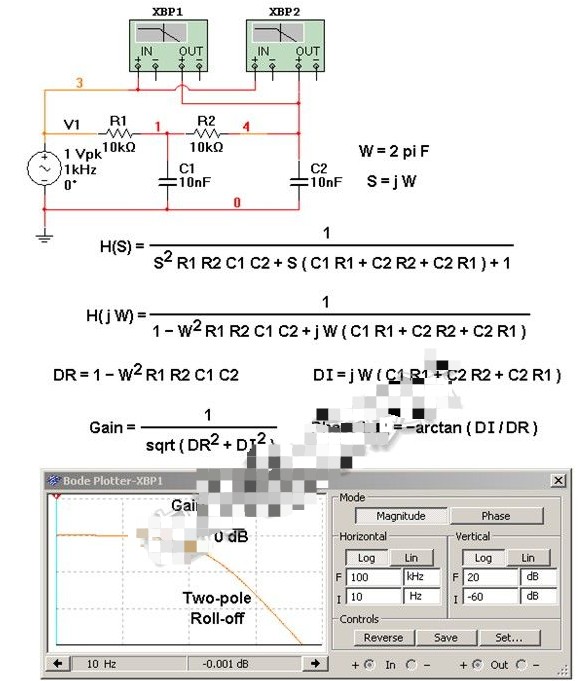
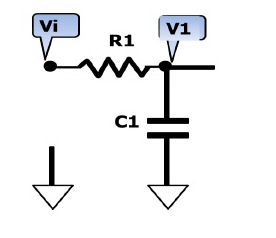
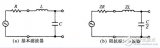
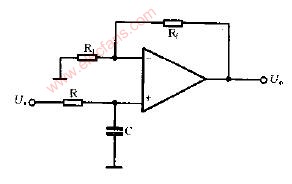
为了改进一阶低通滤波器的频率特性,可采用二阶低通滤波器。一个二阶低通滤波器包含两个RC支路,如图所示为二阶低通滤波器的一般电路。此一般电路对于二阶高通滤波器也同样适用。 图6-2-3所示的滤波器是同相放大器。在图6-2-3中,零频增益为

在节点B可得

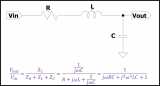
将式(6-2-8)代人式(6-2-6),转变到复频域,可得一般二阶低通滤波器的传递函数为

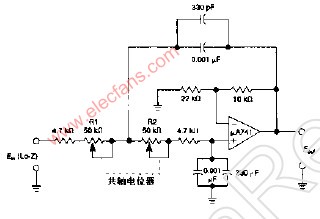
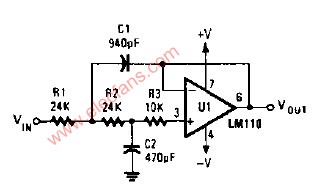
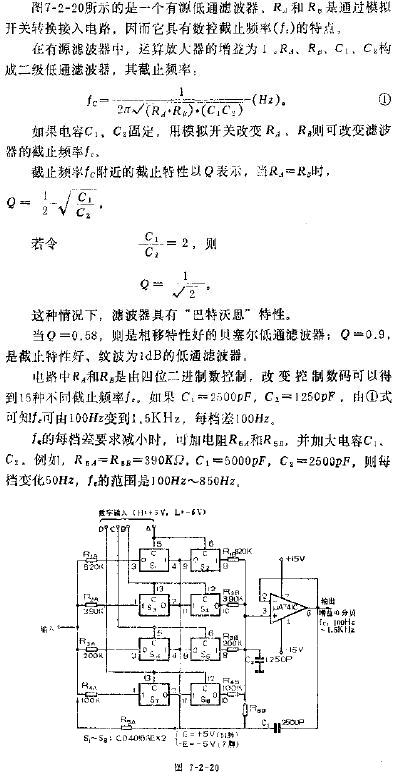
在构成二阶低通滤波器时,只需选择巧,殇,蚝,‰导纳的值即可。例如,当选择Y1=1/R1,Y2=1/R2,Y3=sC1 Y4=sC2时,则构成图6-2-4所示的二阶低通滤波器。

对于上图所示的二阶低通滤波器,其传递函数为


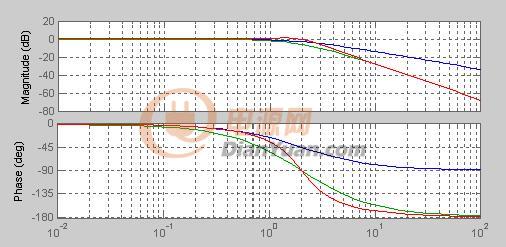
如图6-2-5所示为二阶低通滤波器的幅频特性曲线,其阻带衰减特性的斜率为-40dB/10oct,克服了一阶低通滤波器阻带衰减太慢的缺点。
二阶低通滤波器的各个参数,影响其滤波特性,如阻尼系数苫的大小,决定了幅频特性有无峰值,或谐振峰的高低。如图6=2-6所示为苫对二阶低通滤波器幅频特性的影响。

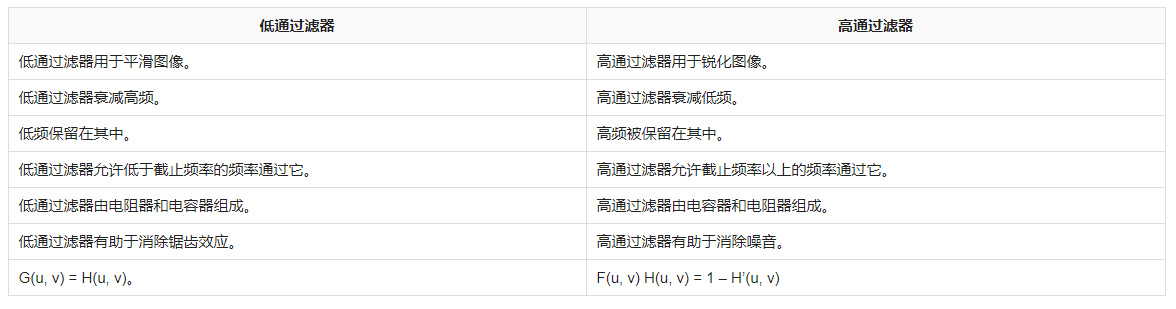
由传递函数判断滤波器
根据系统函数快速判断滤波器类型
(1)死办法,用傅里叶变换求出H(f),在画出幅频特性曲线,看高频部分是不是“通”
(2)用拉氏变换求出H(s),然后记住一句话:分子上有什么就通什么!
举个例子:
H(s)=as/(bs+c)
分子上有“高次”,所以是高通。
这里的“高次”是这个意思:
分母上有s的0次和1次,分子是s的1次,所以是较高的那个,简称“高次”。
H(s)=a/(bs+c)
分子上有“低次”,所以是低通。
H(s)=as^2/(bs^2+cs+d)
分子上有“高次”,所以是高通。
H(s)=a/(bs^2+cs+d)
分子上有“低次”,所以是低通。
H(s)=as/(bs^2+cs+d)
分子上有“中间次”,所以是带通。
第(2)种方法还没找到理论根据,如果将分子分母都除以“高次”,在判断频率从小变化到无穷的情况能理解
如果只有一个零极点,可以根据复平面上零极点位置来判断。
 电子发烧友App
电子发烧友App








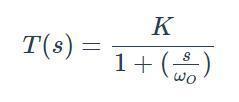
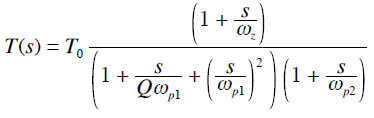
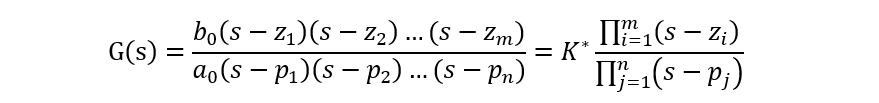
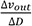
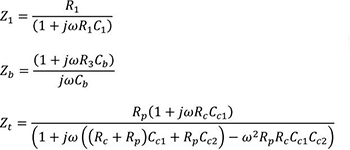
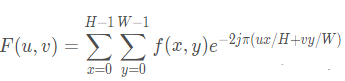




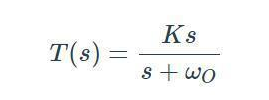

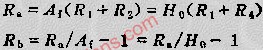

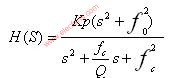










评论