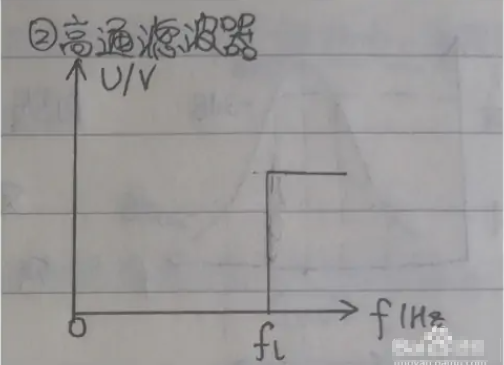
高通滤波器是一种让某一频率以上的信号分量通过,而对该频率以下的信号分量大大抑制的电容、电感与电阻等器件的组合装置。其特性在时域及频域中可分别用冲激响应及频率响应描述。后者是用以频率为自变量的函数表示,一般情况下它是一个以复变量jω为自变量的的复变函数,以H(jω)表示。它的模H(ω)和幅角φ(ω)为角频率ω的函数,分别称为系统的“幅频响应”和“相频响应”,它分别代表激励源中不同频率的信号成分通过该系统时所遇到的幅度变化和相位变化。可以证明,系统的“频率响应”就是该系统“冲激响应”的傅里叶变换。当线性无源系统可以用一个N阶线性微分方程表示时,频率响应H(jω)为一个有理分式,它的分子和分母分别与微分方程的右边和左边相对应。
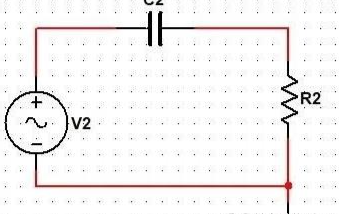
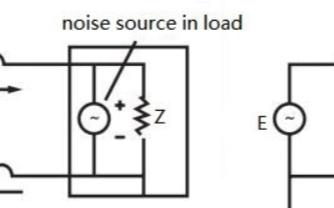
电容和电阻组成的高通滤波器
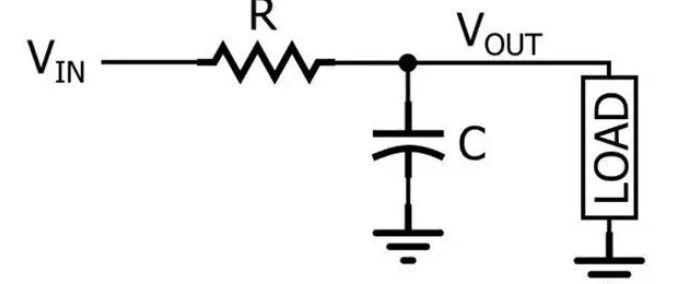
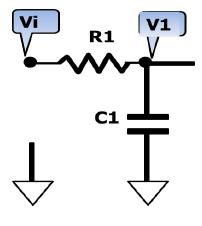
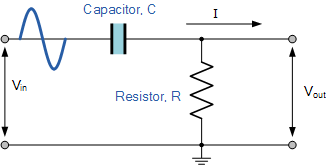
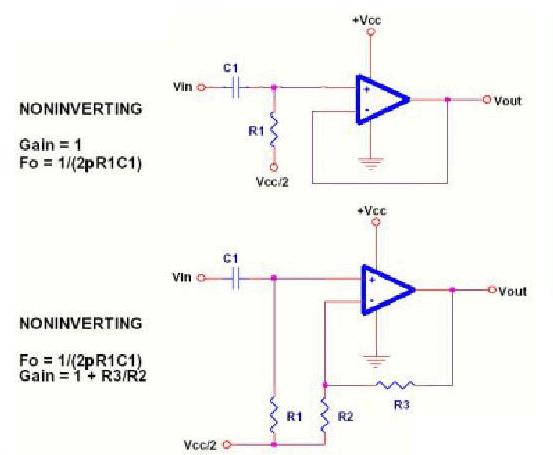
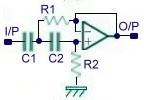
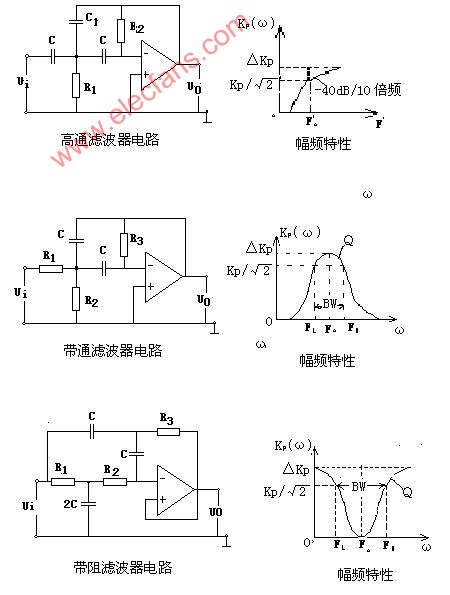
电阻和电容组成的高通滤波器的电路如下:

电阻的阻抗是固定值,为R。
电容的容抗与信号频率f有关,Xc=1/2πfC。
输出电压Uo=Ui*R/(R-jXc)
|Uo|
=Ui*R/√(R^2+Xc^2)
=Ui*R/√(R^2+1/(2πfC)^2)
=Ui/√(1+1/(2πfRC)^2)
记1/2πRC为f0,f0为滤波器的截止频率。
那么,
|Uo|=Ui/√(1+(f0/f)^2)
f=f0时,|Uo|=√2/2*Ui
f趋向0时,|Uo|趋向Ui
f趋向无穷大时,|Uo|趋向0。
f越大,|Uo|越小。
高通滤波器原理解析
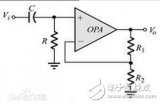
最简单的高通滤波器是“一阶高通滤波器”,它的的特性一般用一阶线性微分方程表示,它的左边与一阶低通滤波器完全相同,仅右边是激励源的导数而不是激励源本身。当较低的频率通过该系统时,没有或几乎没有什么输出,而当较高的频率通过该系统时,将会受到较小的衰减。实际上,对于极高的频率而言,电容器相当于“短路”一样,这些频率,基本上都可以在电阻两端获得输出。换言之,这个系统适宜于通过高频率而对低频率有较大的阻碍作用,是一个最简单的“高通滤波器”。

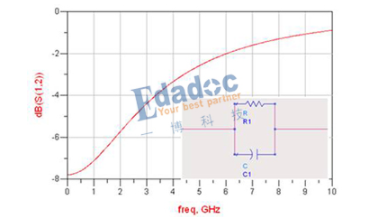
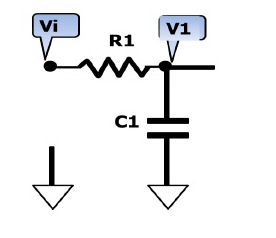
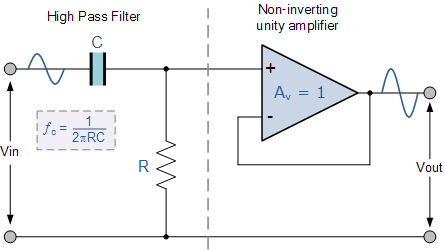
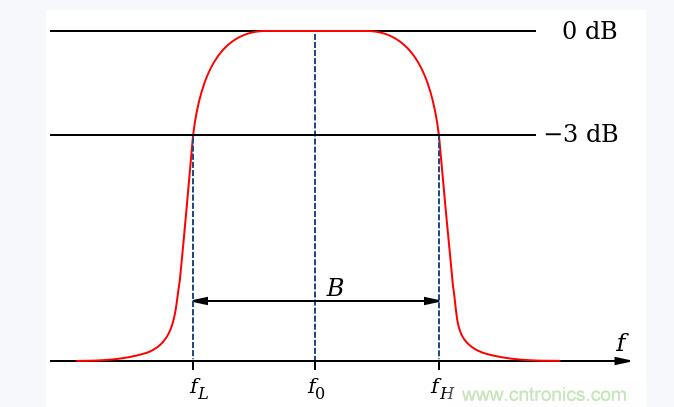
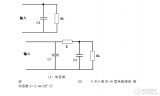
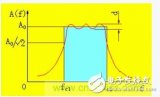
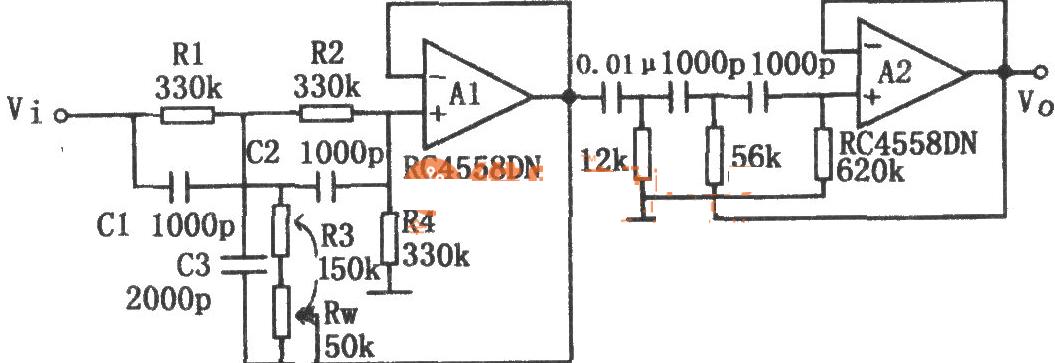
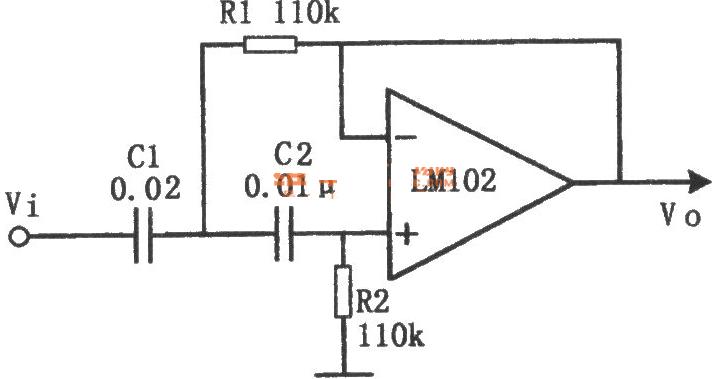
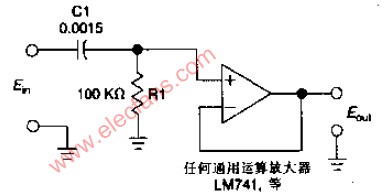
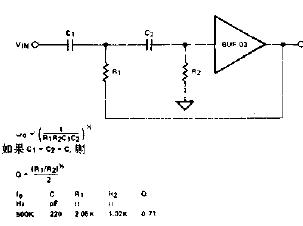
下图是RC元件构成的高通滤波器。图(a)是电路, 图(b)是这一高通滤波器的幅频特性曲线。从这一曲线可以看出,当输入信号Vi中频率低干转折频率f。时,输出受到明显的衰减。高于转折频率f。的信号输出大。

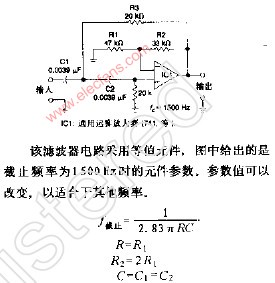
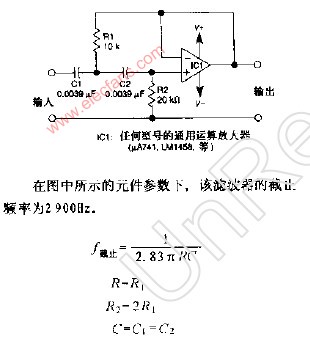
这一电路的工作原理是这样:当频率低于f。的信号输入这一滤波器时,由于C1的容抗很大而受到阻止,输出减小,且频率愈低输出愈小。当频率高于f。的信号输入这一滤波器时,由于C1容抗已很小,故对信号无衰减作用,这样该滤波器具有让高频信号通过,阻止低频信号的作用。这一电路的转折频率f。由下式决定:

 电子发烧友App
电子发烧友App











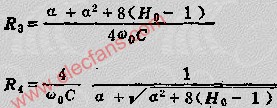
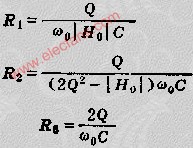
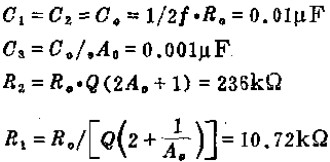












评论