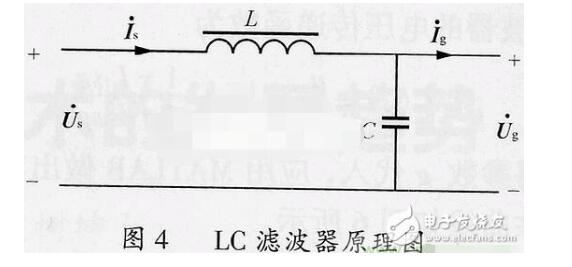
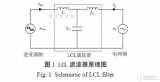
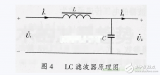
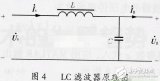
LC滤波器简单设计法
滤波器按照通带特性分类有:低通滤波器(LPF)、高通滤波器(HPF)、带通滤波器(BPF)、带阻滤波器(BRF)、全通滤波器(APF)。关于全通滤波器说明一下,从频率的选择上没有什么特别的作用,因为它基本不具备选频特性,那么这个滤波器有什么用呢?当信号通过这个滤波器时,不会损失任何频率成分,但是信号所包含的各频成分的延时会随频率不同而不同,那么这个滤波器的作用就是改变信号延时,常用在对系统延时进行补偿的场合,也成为移相器。
大家都知道理想的滤波器矩形窗是很难实现的,设计时使用某个函数逼近窗函数来进行设计,这样的滤波器设计方法称为函数型滤波器,根据函数对滤波器进行分类:
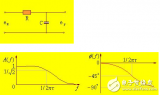
巴特沃斯型滤波器,在通带内响应最为平坦。
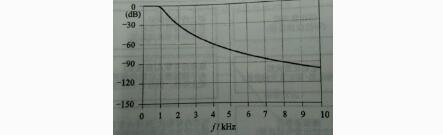
图1巴特沃斯型滤波器
切比雪夫型滤波器(等波纹滤波器),截止频率特别好,群延时特性不太好,通带内有等波纹起伏。
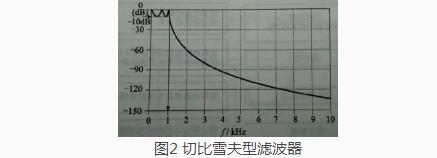
图2切比雪夫型滤波器
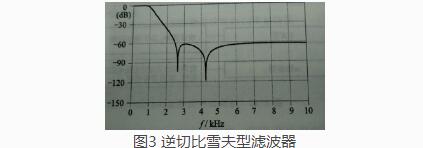
逆切比雪夫型滤波器(巴特沃斯-切比雪夫滤波器),阻带内有零点(陷波点),椭圆滤波器有更好的截止特性,因此并不经常使用。
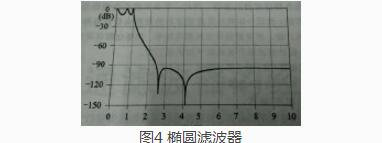
椭圆滤波器(联立切比雪夫滤波器),通带内有起伏,阻带内有零点(陷波点),截止频率比其他滤波器都好,但是对器件要求很高。
贝塞尔型滤波器(延时最平伏滤波器),通带内延时特性最为平坦,截止特性特别差。
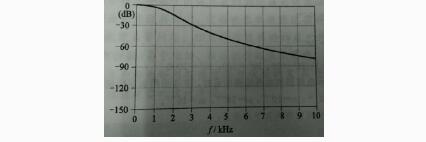
图5贝塞尔滤波器
一般没有特别要求可以选择巴特沃斯滤波器,衰减特性和相位特性都比较好。对衰减特性有要求的情况,可以选择切比雪夫滤波器,但是其相位特性不是很好,对非正弦信号会产生失真。对相位特性由要求的情侣,可以选择贝塞尔滤波器,输出信号一般不会失真。一般滤波器通带内有起伏,则衰减特性会比较好。
低通滤波器设计(LPF)
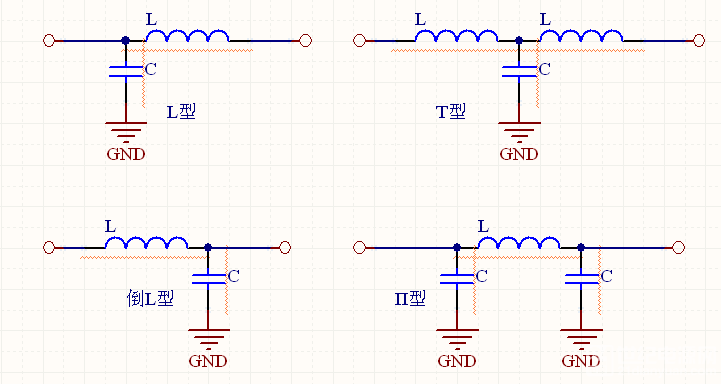
以上基于函数的滤波器设计都是现代模拟滤波器设计的典型方法,比较古典的基于映像参数的设计方法,在设计方法上比较简单,但是相较则截止频率不准确、性能较差。
定K型滤波器,以变量f作为截止频率,计算时只需要将f换成实际截止频率即可。
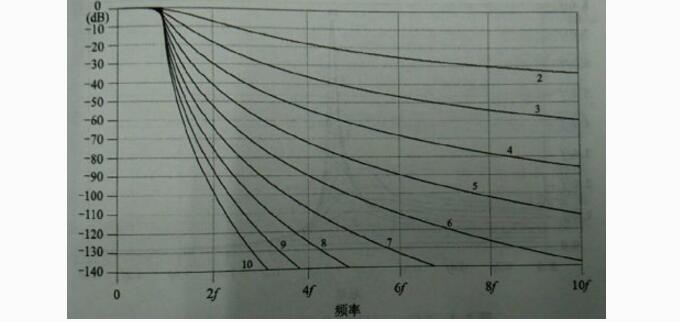
图62~10阶定K型LPF滤波器衰减特性
依据归一化LPF设计定K型滤波器
计算步骤:归一化低通滤波器——》截止频率变换——》特征阻抗变换
M=(待设计滤波器的截止频率)/(基准滤波器的截止频率)
K=(待设计滤波器的特征阻抗)/(基准滤波器的特征阻抗)
电感值计算:L‘=(L*K)/M
电容值计算:C’=C/(K*M)
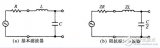
例如:2阶定K型归一化LPF电路,截止频率为1/(2*pi)(pi代表数学圆周率),特征阻抗为1欧姆。
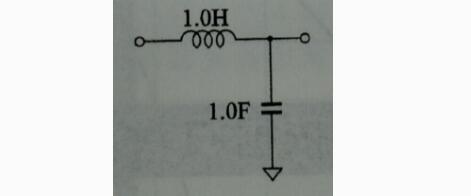
图7归一化2阶定K型LPF
设计截止频率为1KHz,特征阻抗为50欧姆的LPF定K型滤波器。
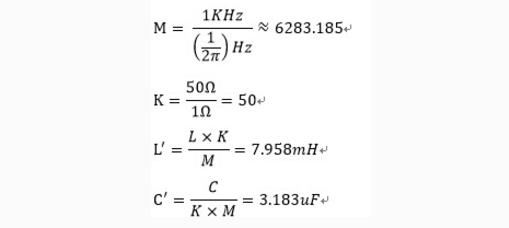
由此可以得到所设计的滤波器:
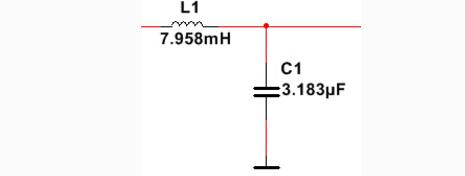
图8截止频率为1KHz,特征阻抗为50欧姆的定K型LPF
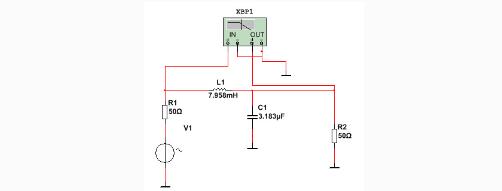
图9仿真电路
可以得到仿真幅频特性曲线:
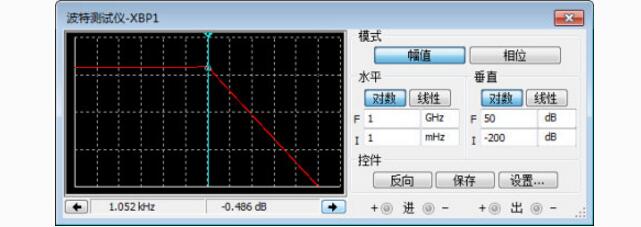
图10仿真幅频特性曲线结果
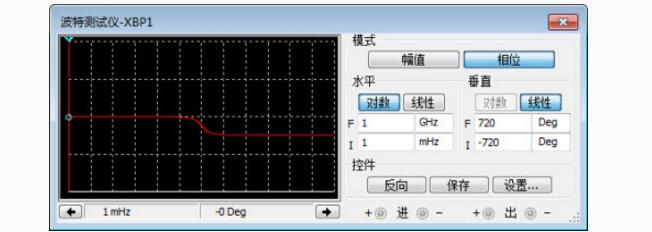
图11仿真相频特性曲线结果
用软件仿真结果还是可以的,对于实际电路就需要进行实际的测试了。
以上过程给大家一个计算方法,对于其他滤波器都可以使用相同的方法,一下提供给大家一些归一化的电路参数,大家在进行计算后先使用仿真软件进行一下仿真,结果有所偏差可以适当更换元件值,最后再实际电路上使用还需要进行实际调整。
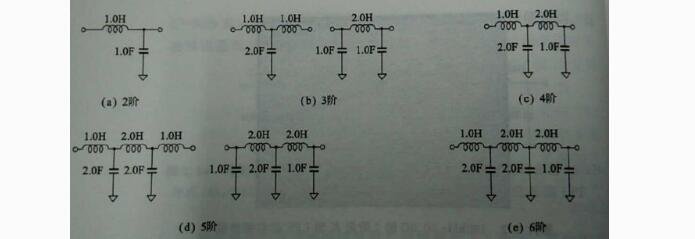
图12定K型LPF归一化电路参数(截止频率都为1/(2*pi),特征阻抗都为1欧姆)
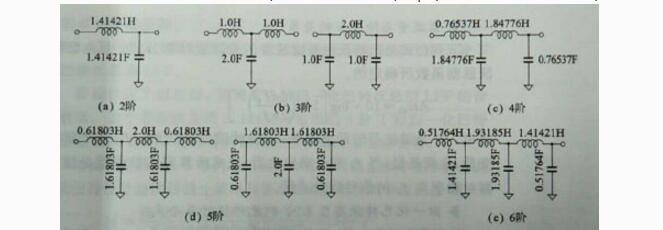
图13巴特沃斯LPF滤波器归一化电路参数(截止频率都为1/(2*pi),特征阻抗都为1欧姆)
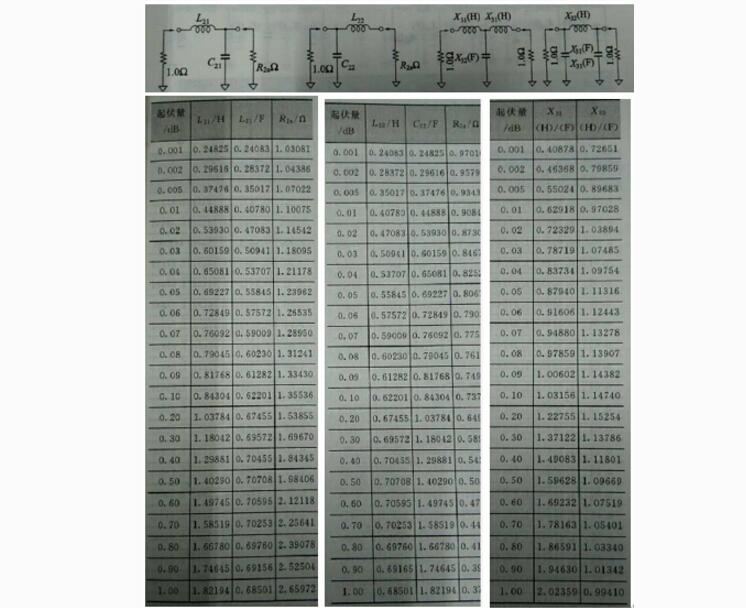
图14切比雪夫LPF归一化电路参数(截止频率都为1/(2*pi),特征阻抗都为1欧姆)
由于切比雪夫滤波器在通带内有起伏,因此多了一个起伏参数,在进行参数选择的时候需要注意与起伏量对应。
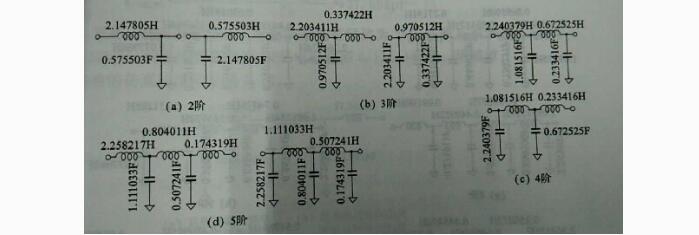
图15贝塞尔LPF归一化电路参数(截止频率都为1/(2*pi),特征阻抗都为1欧姆)
 电子发烧友App
电子发烧友App

























评论