切比雪夫逼近方法
本文给出了物理学家和工程师感兴趣的一般切比雪夫逼近方法(Chehyshev approximation method)的处理方法。详细讨论了切比雪夫多项式(Chebyshev polynomial)的性质, 简要介绍了其在电路理论中的应用.
介绍
在逼近给定函数的各种方法中, 切比雪夫方法(Chebyshev method)对于物理学家和工程师来说是最有吸引力和最重要的方法之一。最初由切比雪夫(P. I. Chebyshev)在机械连杆问题中引入[26], 随着威廉·卡尔(W. Cauer)发表《一种新的滤波器设计方法》[5], 该方法在电气工程中变得特别重要。
本文的目的是回顾关于这个主题的各种文章, 目的是以高度概括的方式介绍材料, 让物理学家和工程师充分理解这个逼近问题。特别强调了切比雪夫多项式, 并简要应用于电路理论。
1. 逼近问题和切比雪夫逼近





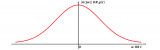
其最大偏差等于2.75。如图1所示。
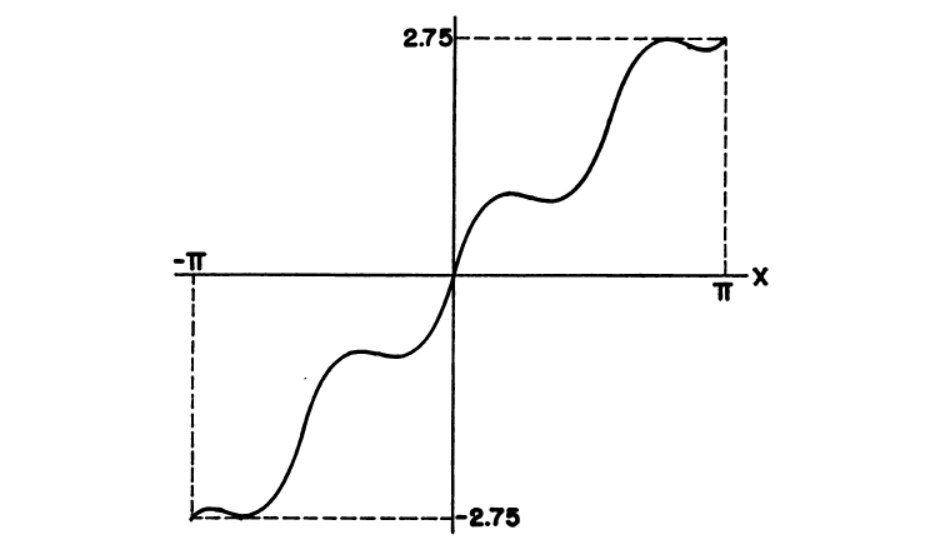

3.切比雪夫多项式




在区间中的切比雪夫多项式

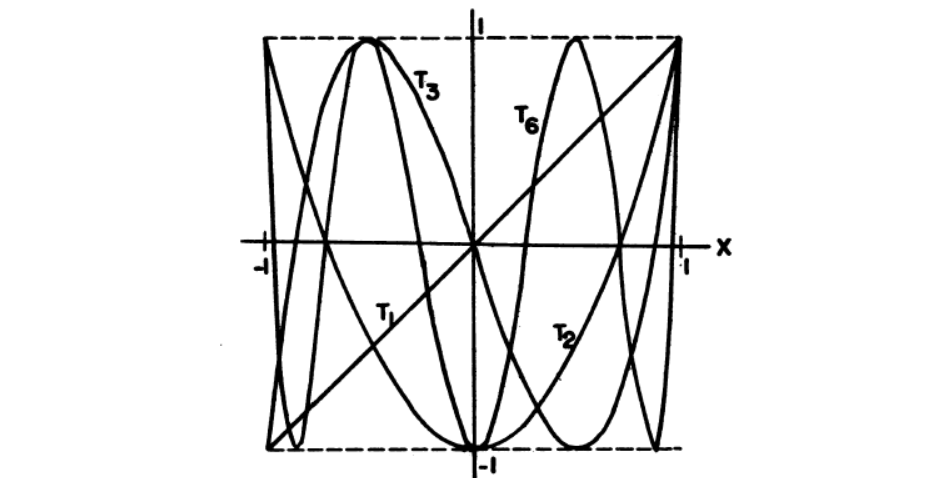


切比雪夫多项式的更多性质

4. 最大化最大根(Maximization of the largest root)。


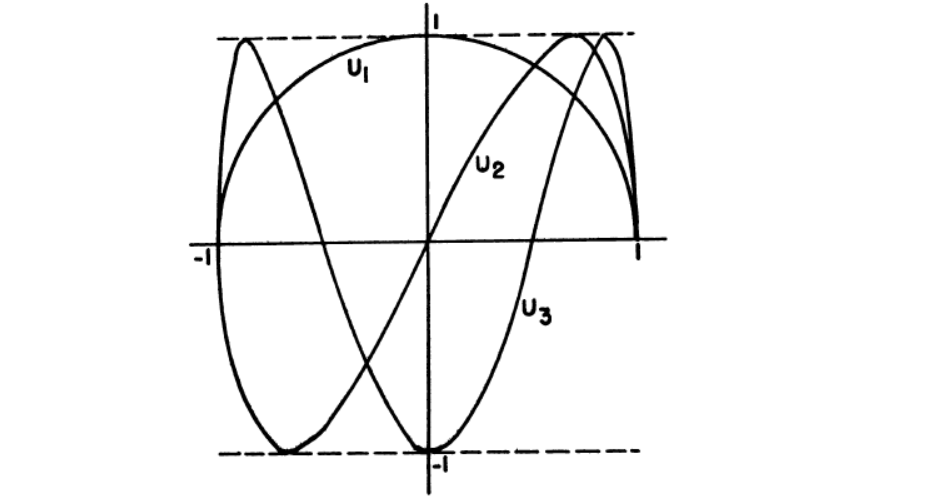


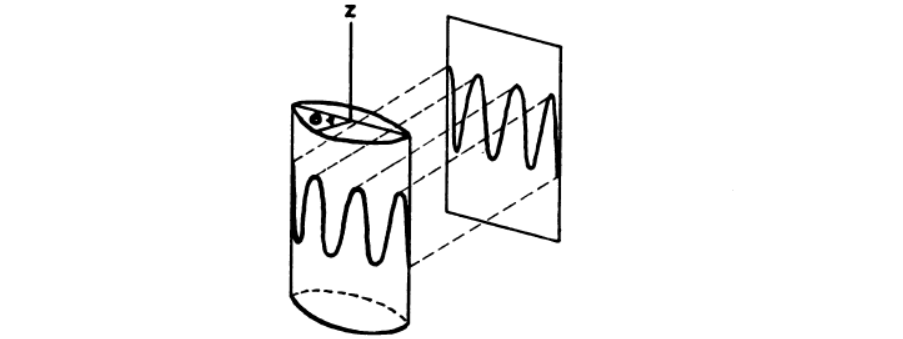

10. 切比雪夫多项式中任意函数的展开。

译注:下图是真空三极管原理图
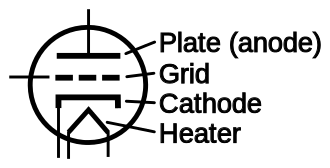

切比雪夫多项式在天线上的应用
天线设计中经常遇到的问题是波束应尽可能窄, 功率增益应最大且旁瓣应相对较小。这些要求通常不容易甚至不可能同时满足, 因此出现了关于什么是最佳方向图模式的问题。对于本次讨论, 我们将把具有指定的旁瓣电平具有最小波束宽度的方向图称为最佳方向图。
要确定获得最佳方向图的方法, 考虑一组n个各向同性点源, 它们的间距均匀分布并且都处于同一相位, 如图5所示。
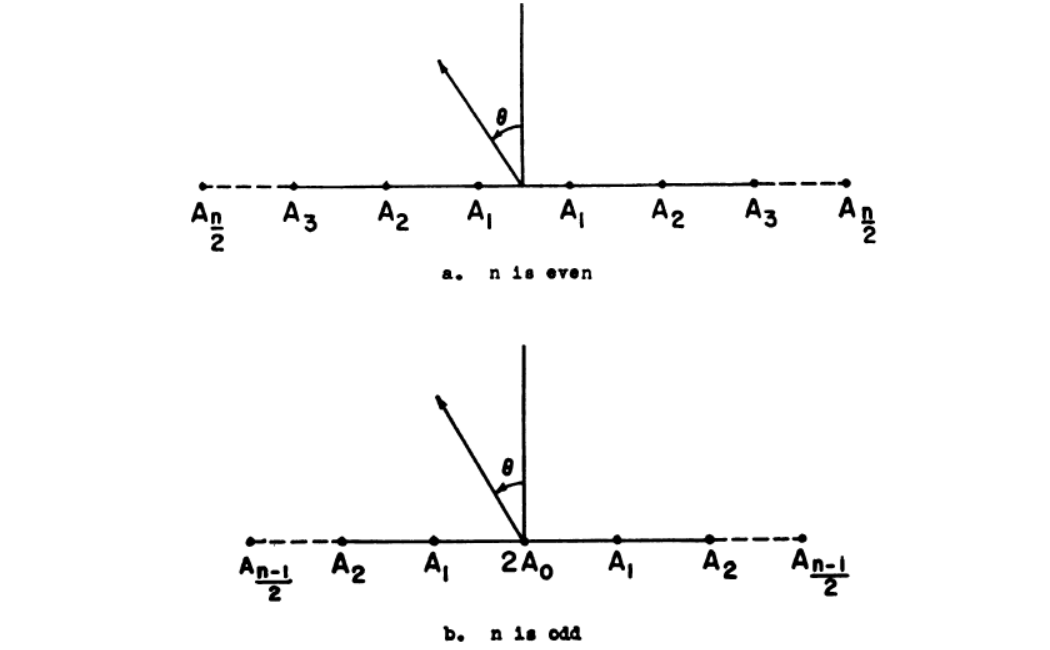


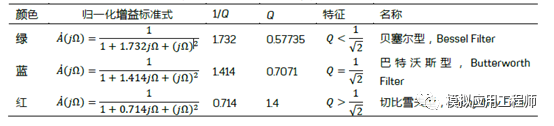
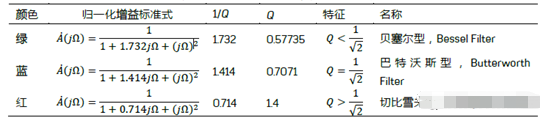
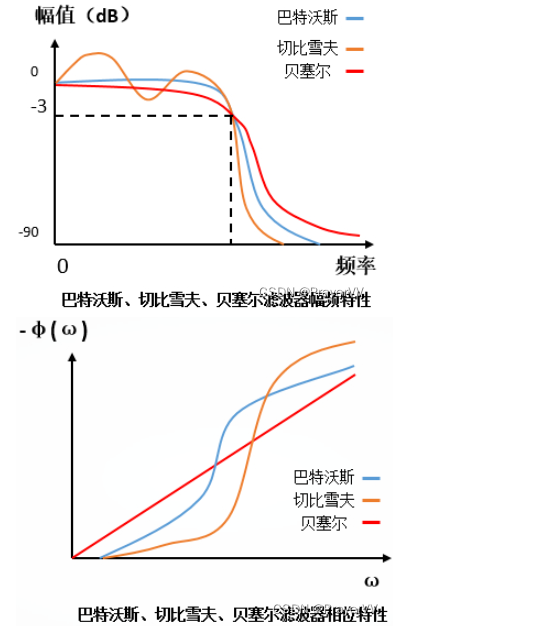
切比雪夫项式与滤波器的关系
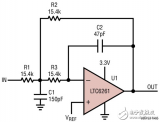
考虑图6中所示的电路网络。
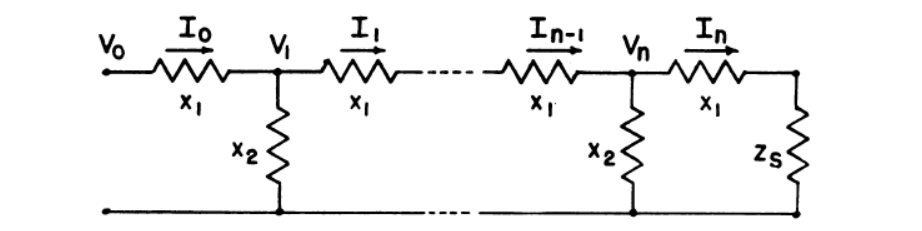
图6. 以梯形方式连接的有限被动元件网络

定向耦合器的应用
F. Bolinder已经指[2]出, 如果希望在定向耦合器中最大化通带宽度与通带中反射波电平的比率, 那么对于给定数量的元件, 人们将以这样一种方式选择耦合因子, 即反向电流值随距离的变化将是以切比雪夫多项式描述。
审核编辑:刘清
 电子发烧友App
电子发烧友App





















评论