提到傅里叶变换，你是不是又想起了大学课程里被它支配的恐惧。其实，傅里叶分析不仅仅是一个数学工具，更是一种可以彻底颠覆一个人以前世界观的思维模式。如果用方程写一部科学史，傅里叶变换必然拥有位置，它
2023-09-11 11:21:06
289 
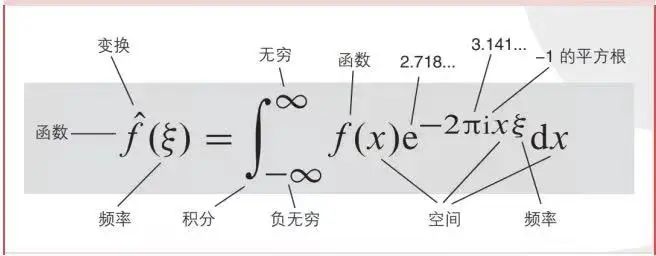
傅里叶变换与拉普拉斯变换的联系解读 傅里叶变换和拉普拉斯变换都是数学中非常重要的分析工具。它们都在不同的领域中发挥着重要作用。 傅里叶变换是一种将时间域信号转换成频率域信号的技术。它是通过将信号
2023-09-07 17:04:19219 傅里叶变换和离散傅里叶变换的关系 傅里叶变换（Fourier Transform）是一种将时间域（或空间域）的信号转换为频率域（或波数域）的信号的数学工具。而离散傅里叶变换（Discrete
2023-09-07 17:04:15330 短时傅里叶变换和小波变换差别 短时傅里叶变换（short-time Fourier transform，STFT）和小波变换（wavelet transform）是两种常见的信号处理技术，它们在频域
2023-09-07 17:04:12341 小波变换与傅里叶变换的区别和联系 1. 傅里叶变换和小波变换的定义 傅里叶变换（Fourier Transform，简称FT）是一种将信号在时域上的函数转变为频域上的函数的方法，对于连续时间信号
2023-09-07 17:04:07332 为什么有四种形式的傅里叶变换 傅里叶变换是一种十分重要的数学工具，它可以将函数从时域（即时间域）转换到频域，从而能够帮助人们更好地理解信号的特性。在傅里叶变换的研究过程中，出现了几种不同的变形方式
2023-09-07 17:04:04189 傅里叶变换重要公式总结 傅里叶变换公式常用公式 傅里叶变换是一种重要的数学工具，它可以将任意周期函数分解成一系列正弦函数或余弦函数的叠加形式。这些正弦函数和余弦函数被称为频率分量，它们的幅度和相位
2023-09-07 16:53:083859 傅里叶变换公式理解 傅里叶变换是一种在数学、物理、工程和其他科学领域中常用的工具，它是一种将一个函数从时域转换到频域的方法。傅里叶变换可以将一个复杂的函数表示成一个频域上各种周期函数的叠加，从而
2023-09-07 16:53:06534 傅里叶变换和反变换公式 傅里叶变换和反变换在信号处理领域中被广泛应用。傅里叶变换是将一个时域信号转换为频域信号的过程，而傅里叶反变换则是将一个频域信号转换为时域信号的过程。这篇文章将详细讲解
2023-09-07 16:53:042916 傅里叶变换的实现方法 傅里叶变换是一种将信号在时间域和频率域之间相互转换的数学工具。它的实现方法有很多种，其中最常见的是离散傅里叶变换（DFT）和快速傅里叶变换（FFT）。 离散傅里叶变换是一种将
2023-09-07 16:47:52173 傅里叶变换公式总结 傅里叶变换是一种将时域信号转换为频域信号的数学方法。它是通过将一个连续或离散的时域信号分解成一系列相位和幅度不同的正弦和余弦波形式，然后将它们表示到频域中，以获得更多的信息
2023-09-07 16:47:461222 傅里叶变换和傅里叶逆变换的关系 傅里叶变换和傅里叶逆变换是信号处理领域中极具重要性的数学工具，它们被广泛应用于很多领域，例如音频、图像处理、通信等。 傅里叶变换是将一个信号在时域（即时间或空间）上
2023-09-07 16:43:47581 正弦函数的傅里叶变换 正弦函数是数学中一种广泛应用的基本函数，其在傅里叶分析中也是具有重要作用的函数之一。在实际应用中，我们常常需要将正弦函数进行傅里叶变换，以求得自变量函数在频域上的表现，从而更好
2023-09-07 16:35:07836 傅氏变换和傅里叶变换的区别联系 傅氏变换和傅里叶变换是信号处理中常用的两种变换方法，它们有着不同的作用和特点。傅氏变换主要应用于连续时间信号的频域分析，而傅里叶变换则主要用于离散时间信号的频域分析
2023-09-07 16:35:05195 傅里叶变换的本质及物理意义 常用傅里叶变换性质 傅里叶变换是一种重要的数学工具，通过将一个复杂的函数表示为一系列简单的正弦余弦函数之和，可以在许多领域应用，包括信号处理、图像处理、物理学等。在本文
2023-09-07 16:30:33544 傅里叶变换时域平移怎么理解 傅里叶变换是一种非常重要的数学工具，在信号处理、图像处理、通信技术等领域中广泛应用。其中，时域平移是傅里叶变换中一个重要的概念，需要深入理解。 时域平移的基本概念 时域
2023-09-07 16:29:40330 傅里叶变换频移公式 傅里叶变换是一种将信号从时域转换到频域的数学工具。它可以将一个信号分解成一系列正弦和余弦波的和，这些正弦和余弦波的振幅和相位可以描述信号在频域中的特性。傅里叶变换是数字信号处理
2023-09-07 16:29:36451 冲激函数时移后的傅里叶变换 傅里叶变换（Fourier transform）是数学中的一种重要的分析工具，它能够将一个时域（time domain）或空域（space domain）中的函数转换
2023-09-07 16:23:25396 短时傅里叶变换特点 短时傅里叶变换的意义 短时傅里叶变换（Short-time Fourier Transform, STFT）是一种时频分析方法，它把信号在时间和频率上进行分解，可以对信号的短时
2023-09-07 16:23:22441 傅里叶变换的时移特性 傅里叶变换是一种非常重要的数学工具，可以将任何周期性信号或非周期性信号进行频域分析，从而在通信、电子工程等领域中得到广泛应用。傅里叶变换能够将信号从时域（时间域）转换到频域
2023-09-07 16:23:19738 对图像进行傅里叶变换的意义 傅里叶变换是一种将一个信号分解成其频率分量的方法，它在信号处理、图像处理、电信领域、计算机视觉领域等方面都有着广泛的应用。在图像处理领域中，傅里叶变换可以将图像从空间域
2023-09-07 16:18:56353 傅里叶变换的数学意义 傅里叶变换是一种数学工具，它是一种将一个函数在一个频域转换为另一个函数在另一个频域中的操作。傅里叶变换起源于1807年，由法国数学家让·巴蒂斯特·约瑟夫·傅里叶提出，它是一种将
2023-09-07 16:18:51148 傅里叶变换基本性质 傅里叶变换本质 傅里叶变换的应用 傅里叶变换是现代数学、物理学、工程学等领域中非常重要的一种数学工具和基本理论。在信号处理、图像处理、通信技术、音乐分析、光学、医学、天气预报等
2023-09-07 16:18:492334 傅里叶变换通俗理解 对傅里叶变换的理解 傅里叶变换是一种数学工具，它可以将一个函数从时域（时间域）转换到频域（频率域）。在数学、物理学、工程学和计算机科学等领域它被广泛应用，例如数字信号处理
2023-09-07 16:14:41570 傅里叶变换的目的和意义 傅里叶变换几何意义 傅里叶变换是一种重要的数学工具和分析方法，它在信号处理、图像处理、音频处理等领域有着广泛的应用。它的目的是将一个时域信号转换为频域信号，从而更好地理
2023-09-07 16:14:39307 傅里叶变换十大公式 傅里叶变换的十大性质 傅里叶变换是一种重要的数学工具，在许多领域中都有广泛的应用。傅里叶变换可以将一个时域信号转化为频域信号，分析不同频率成分在信号中的占比情况。由于傅里叶变换
2023-09-07 16:14:361210 傅里叶变换对信号处理的意义 傅里叶变换是一种基本的数学工具，它经常用于信号处理中。在这篇文章中，我们将探讨傅里叶变换的意义和应用。 傅里叶变换的定义是将一个函数表示为它的频域表示。傅里叶变换将
2023-09-07 16:14:33252 傅里叶变换有多伟大?傅里叶变换告诉我们如何解决问题 傅里叶变换是一种数学工具，它可以将一个函数分解成一系列振幅和相位的频率，这些频率在某些领域 （如信号处理、图像处理和物理学等）中被广泛
2023-09-07 16:14:31165 傅里叶变换的意义和理解 傅里叶变换是一种将一个信号在频域中进行分解的数学工具，它将一个信号分解为不同频率的正弦和余弦波的叠加。傅里叶变换的基本概念源于法国数学家约瑟夫·傅里叶，而其在现代通信、图像
2023-09-07 16:08:423549 对于一个离开课堂十余年的射频工程师来说，傅里叶变换已经不知道埋藏在脑子里的那个角落，或者根本就没在脑子里停留过。但无论如何，傅里叶变换对现在通信的重要性还是不言而语。当我们已经习惯用频域去描述一个信号的时候，你可曾思考过其真实的样子到底是什么？ 为什么这几个短短的频谱就可以描述一个信号 ？
2023-08-10 09:55:51341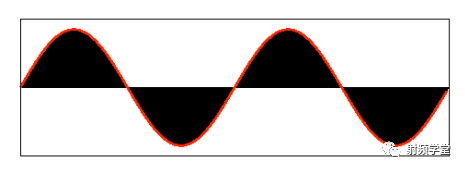 
快速傅里叶变换 (Fast Fourier Transform，FFT), 即利用计算机计算离散傅里叶变换（DFT)的高效、快速计算方法的统称，简称FFT。
2023-07-20 16:46:231159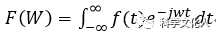 
傅里叶变换是将按时间或空间采样的信号与按频率采样的相同信号进行关联的数学公式。
2023-07-19 17:47:301830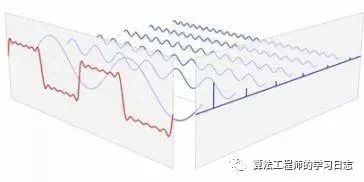 
学习傅里叶变换需要面对大量的数学公式，数学功底较差的同学听到傅里叶变换就头疼
2023-07-07 14:15:10217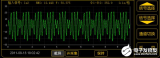 
机器学习和深度学习中的模型都是遵循数学函数的方式创建的。从数据分析到预测建模，一般情况下都会有数学原理的支撑，比如：欧几里得距离用于检测聚类中的聚类。 傅里叶变换是一种众所周知的将函数从一个域转换
2023-06-14 10:01:16420 
傅里叶变换是一种在各个领域都经常使用的数学工具。这个网站将为你介绍傅里叶变换能干什么，为什么傅里叶变换非常有用，以及你如何利用傅里叶变换干漂亮的事。
2022-07-10 10:37:531341 各位如何用LABVIEW做一个关于离散傅里叶变换？？！！！
2012-04-08 21:59:31
周期矩阵脉冲信号傅里叶变换问题求解
2021-06-26 14:49:06
0 原信号的不同类型，傅里叶变换可以分为四种类别： (1)非周期性连续信号傅里叶变换 (2)周期性连续信号傅里叶级数 (3)非周期性离散信号离散时域傅里叶变换 (4)周期性离散信号离散傅里叶变换 快速傅里叶变换(FFT)，是利用计算机计算离散傅里叶
2020-11-09 16:52:4012009 
学习傅里叶变换需要面对大量的数学公式，数学功底较差的同学听到傅里叶变换就头疼。事实上，许多数学功底好的数字信号处理专业的同学也不一定理解傅里叶变换的真实含义，不能做到学以致用 事实上，傅里叶变换
2020-10-10 18:03:1721666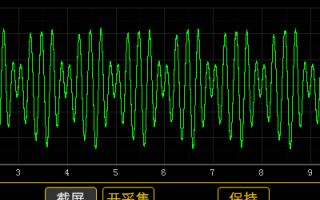 
傅里叶变换是数字信号处理领城种很重要的算法。傅里叶表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理的傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该
2019-04-30 08:00:002 主要内容：
1.傅里叶变换
2.傅里叶变换的特殊形式
3.傅里叶变换的物理意义
4.傅里叶变换存在的条件
2018-03-05 11:08:043 主要内容：
1.正弦信号的傅里叶变换
2.一般周期信号的傅里叶变换
3.如何由F0(ω)求F(nω1)
4.单位冲激序列的傅氏变换
5.周期矩形脉冲序列的傅氏变换
2018-03-05 10:59:052 详细讲述傅里叶变换和小波变换原理
2018-01-16 14:34:429 小波变换与傅里叶变换有什么区别吗？小波变换与傅里叶变换哪个好？我们通过小波变换与傅里叶变换的详细解读、小波变换与傅里叶变换的区别、傅里叶变换缺点方面来解析。
2018-01-13 11:02:2213781 
抽样信号的傅里叶变换
2017-12-06 14:36:013 傅里叶变换的性质
2017-12-06 14:35:0059 快速傅里叶变换 （fast Fourier transform）,即利用计算机计算离散傅里叶变换（DFT）的高效、快速计算方法的统称，简称FFT。快速傅里叶变换是1965年由J.W.库利
2017-11-27 16:23:011408 傅里叶级数对周期性现象做数学上的分析傅里叶变换可以看作傅里叶级数的极限形式，也可以看作是对周期现象进行数学上的分析。除此之外，傅里叶变换还是处理信号领域的一种很重要的算法。要想理解傅里叶变换算法的内涵，首先要了解傅里叶原理的内涵。
2017-11-24 14:32:4237881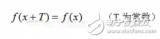 
第三章-离散傅里叶变换-作业
2016-12-28 14:23:300 第三章-离散傅里叶变换
2016-12-28 14:23:303 第3章--离散傅里叶变换(DFT)
2016-12-28 14:23:302 【检测技术】 快速傅里叶变换，测控技术仪器必备课程，喜欢学习的朋友可以下载学习学习。
2016-11-18 16:53:481 《OpenCV3编程入门》书本配套源代码:离散傅里叶变换
2016-06-06 15:39:445 关于短时傅里叶变换的原理及其在通信的应用。
2016-05-17 16:41:515 见过的介绍傅里叶变换的很好的文章，通俗易懂，转发的，学习。
2016-04-29 14:12:1410 傅里叶变换的深刻理解结合书本，会有更好的效果
2015-11-26 11:29:1253 离散傅里叶变换是一种在时域和频域均离散的傅里叶变换.
2011-02-23 09:30:1049 序列的傅里叶变换(DTFT) :DTFT:Discrete-time Fourier transform为研究离散时间系统的频率响应作准备，从抽样信号的傅里叶变换引出：二．傅氏变换、拉氏变换、z变换的关系1. 三
2009-09-30 19:38:2536 非周期信号的傅里叶变换
前面已讨论了周期非正弦信号的傅里叶级数展开，下面来分析非周期信号的傅里叶变换。当周期
2009-07-27 10:23:307992 离散傅里叶变换及其快速算法离散傅里叶变换 (Discrete Fourier Transform，DFT)是时间函数是离散的，而且频谱函数也是离散的变换。3. 1 讨论周期序列的 傅里叶级数及其性质。
2008-10-30 12:54:5433 从本章开始由时域转入变换域分析，首先讨论傅里叶变换。傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生的，这方面的问题也称为傅里叶分析（频域分析）。将信号
2008-08-05 11:49:3750 傅里叶变换公式
2007-11-29 12:52:35494 傅里叶变换详解
2007-11-29 12:48:014
电子发烧友App
工商网监
评论