石英谐振器的数学描述
在压电材料中,电流和电压与弹性位移和应力的耦合
{T} = [c] {S} - [e] {E}
{D} = [e] {S} + [∈] {E}
式中:
{T} = 应力张量, [c] =弹性刚度矩阵,{S} =应变张量, [e] =压电矩阵
{E} = 电场矢量, {D} =电位移矢量, [∈] = 介电矩阵
对于线性压电材料

式中:
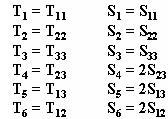
石英的电弹性矩阵
除了各主斜线完全相易,其它各线连接
数值方程。
○表示●的负值
◎表示数值方程的两倍
×表示1/2(C11-C12)
独立的非零常数的数量取决于晶体的对
称性。对于石英(三角晶系,32 中晶类),
 有10 个独立的线性常数:6 个弹性常数,2 个压电常数和2 个介电常数。这些“常数”均与
有10 个独立的线性常数:6 个弹性常数,2 个压电常数和2 个介电常数。这些“常数”均与
温度、应力、坐标系有关。
为了描述谐振器的性能,必须在晶片表面相当的电和机械边界条件下连续求解牛顿运动
定律和麦克斯韦微分方程*

这些方程很“凌乱”,对实际上可以实现的三维谐振器,决不能以闭合形式求解。几乎
所有的理论文章均采用近似值。
某些最重要的谐振器现象(如加速度灵敏度)是由于非线性效应引起的。石英具有许多
高阶常数,例如14 个三阶弹性常数和23 个四阶弹性常数,以及16 个三阶压电系数;非线
性方程很“凌乱”。
*磁场效应一般可以忽略不计;石英是非磁性的,但磁场能够影响安装结构和电极。
 电子发烧友App
电子发烧友App



























评论