1.1 概述
1 . 1 . 1 数字信号和数字电路
1、 数字信号与模似信号
2、 模拟电路与数字电路
1 . 1 . 2 数字电路的分类
1、 按电路类型分类
2、 按集成度分类
3、 按半导体的导电类型分类
1 . 1 . 3 数字电路的优点
1、 易集成化
2、 抗干扰能力强,可靠性高
3、 便于长期存贮
4、 通用性强,成本低,系列多
5、 保密性好
1 .1 .4 脉冲波形的主要参数
1.脉冲幅度Um
2.脉冲上升时间
3.脉冲下降时间
4.脉冲宽度
5.脉冲周期
6.脉冲频率
7.占空比q
1.2 数制和码制
1 . 2 . 1 数 制
一、十进制
二、二进制
三、八进制和十六进制
1 .2 .2 不同数制间的转换
一、各种数制转换成十进制
二、十进制转换为二进制
三、二进制与八进制、十六进制间相互转换
1 .2 .3 二进制代码
一、二-十进制代码
8421码、5421码和余3码
二、可靠性代码
1.格雷码
2.奇偶校验码
作业:P10 2.(1)(3)3.(1)(3)4. (4)5. (4)6. (4)
7.(4)
第1章 绪 论
1.1 概述
1 . 1 . 1 数字信号和数字电路
电信号 — 随时间变化的电流或电压。
1、数字信号与模似信号
模拟信号 — 幅度随时间连续变化
数字信号 — 断续变化(离散变化),时间上离散幅值上整量化,多采用0、1二种数值组成又称二进制信号。
举例P1图1.1.1。与同学讨论离散信号。

2、模拟电路与数字电路
模拟电路 — 传输或处理模拟信号的电路,如:电压、功率放大等;
数字电路 — 处理、传输、存储、控制、加工、算运算、逻辑运算、数字信号的电路。
如测电机转速:电机-光电转换-整形-门控-计数器-译码器-显示
时基电路
1 . 1 . 2 数字电路的分类
微电子技术的迅猛发展导致了数字电路的飞速发展。
1、 按电路类型分类
(1)组合逻辑电路 输出只与当时的输入有关,如:编码器、加减法器、比较器、数据选择器。
(2)时序逻辑电路 输出不仅与当时的输入有关,还与电路原来的状态有关。
如:触发器、计数器、寄存器
2、 按集成度分类
SSI →MSI→LIS→VLSI
表1.1.1 数字集成电路分类
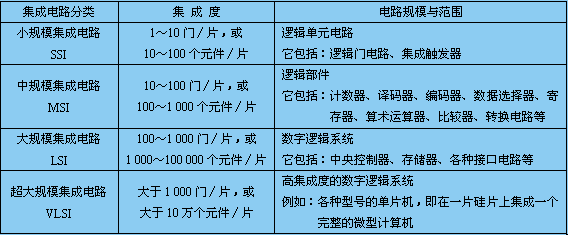
3、 按半导体的导电类型分类
(1) 双极型电路
(2) 单极型电路
1 . 1 . 3 数字电路的优点
1、 易集成化。 两个状态“0”和“1”,对元件精度要求低。
2、 抗干扰能力强,可靠性高。 信号易辨别不易受噪声干扰。
3、便于长期存贮。 软盘、硬盘、光盘。
4、通用性强,成本低,系列多。
(国际标准)TTL系例数字电路、门阵列、可编程逻辑器件。
5、保密性好。 容易进行加密处理。
1 . 1 . 4 脉冲波形的主要参数
在数字电路中,加工和处理的都是脉冲波形,而应用最多的是矩形脉冲。
图1 . 1 . 2 脉冲波形的参数

1.脉冲幅度 。 脉冲电压波形变化的最大值,单位为伏(V)。
2.脉冲上升时间。 脉冲波形从0.1Um上升到0.9Um所需的时间。
3.脉冲下降时间 。脉冲波形从0.9Um下降到0.1Um所需的时间。
脉冲上升时间tr 和下降时间tf 越短,越接近于理想的短形脉冲。单位为秒(s)、毫秒(ms)、微秒( us)、纳秒(ns)。
4.脉冲宽度 。 脉冲上升沿0.5Um 到下降沿0.5Um 所需的时间,单位和 tr、tf 相同。
5.脉冲周期T。 在周期性脉冲中,相邻两个脉冲波形重复出现所需的时间,单位和tr 、tf 相同。
6.脉冲频率f:每秒时间内,脉冲出现的次数。 单位为赫兹(Hz)、千赫兹(kHz)、兆赫兹(MHz),f =1∕T。
7.占空比q:脉冲宽度 与脉冲重复周期T的比值。q = ∕T。
它是描述脉冲波形疏密的参数。
1.2 数制和码制
1 . 2 . 1数 制
一、十进制
1、表示法
![]()
与同学讨论二、八、十六进制的表示方法及特点
二、二进制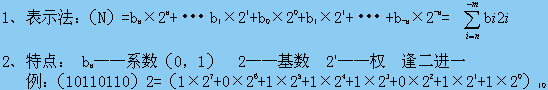
三、八进制和十六进制
1.八进制
逢八进一;系数0~7 ;基数8; 权8 n。
2.十六进制
逢十六进一;系数:0~9、A、B、C、D、E、F;基数16;权16n。
表1.2.1 十进制、二进制、八进制、十六进制对照表
1 . 2 . 2 不同数制间的转换
一、各种数制转换成十进制
二进制、八进制、十六进制转换成十进制时,只要将它们按权展开,求出各加权系数的和,便得到相应进制数对应的十进制数。
例:

二、十进制转换为二进制
将十进制数的整数部分转换为二进制数采用“除2取余法”;
将十进制小数部分转换为二进制数采用“乘2取整法”。
例1.1.1将十进制数(107.625)10转换成二进制数。
将十进制数的整数部分转换为二进制数采用“除2取余法”,它是将整数部分逐次被2除,依次记下余数,直到商为0。第一个余数为二进制数的最低位,最后一个余数为最高位。
解:① 整数部分转换
所以,![]()
②小数部分转换
将十进制小数部分转换为二进制数采用“乘2取整法”,它是将小数部分连续乘以2,取乘数的整数部分作为二进制数的小数。
由此可得十进制数(107.625)10对应的二进制数为
(107.625)10=(1101011.101)2
三、二进制与八进制、十六进制间相互转换
1.二进制和八进制间的相互转换
(1) 二进制数转换成八进制数。
二进制数转换为八进制数的方法是:整数部分从低位开始,每三位二进制数为一组,最后不足三位的,则在高位加0补足三位为止;小数点后的二进制数则从高位开始,每三位二进制数为一组,最后不足三位的,则在低位加0补足三位,然后用对应的八进制数来代替,再按顺序排列写出对应的八进制数。
例1.1.2 将二进制数(11100101.11101011)2转换成八进制数。
(11100101.11101011)2=(345.726)8
(2) 八进制数转换成二进制数。
将每位八进制数用三位二进制数来代替,再按原来的顺序排列起来,便得到了相应的二进制数。
例1.1.3 将八进制数(745.361)8转换成二进制数。
(745.361)8= (111100101.011110001)2
2.二进制和十六进制间的相互转换
(1) 二进制数转换成十六进制数。
二进制数转换为十六进制数的方法是:整数部分从低位开始,每四位二进制数为一组,最后不足四位的,则在高位加0补足四位为止;小数部分从高位开始,每四位二进制数为一组,最后不足四位的,在低位加0补足四位,然后用对应的十六进制数来代替,再按顺序写出对应的十六进制数。
例1.1.4 将二进制数(10011111011.111011)2转换成十六进制数。
(10011111011.111011)2=(4FB.EC)16
(2)十六进制数转换成二进制数。
将每位十六进制数用四位二进制数来代替,再按原来的顺序排列起来便得到了相应的二进制数。
例1.1.5 将十六进制数(3BE5.97D)16转换成二进制数。
(3BE5.97D)16=(11101111100101.100101111101)2
1.2.3 二进制代码
讨论:码的作用;BCD码。
一、二-十进制代码
将十进制数的0~9十个数字用二进制数表示的代码,称为二-十进制码,又称BCD码。
表1.2.2 常用二-十进制代码表(重点讲解8421码、5421码和余3码)

注意:含权码的意义。
二、可靠性代码
1.格雷码
表1.2.3 格雷码与二进制码关系对照表

2.奇偶校验码
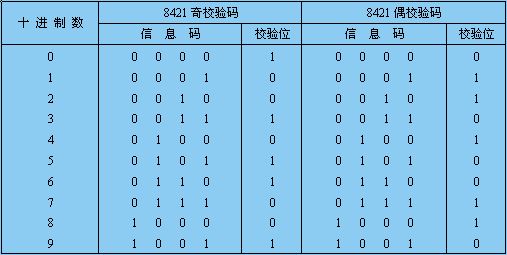
为了能发现和校正错误,提高设备的抗干扰能力,就需采用可靠性代码,而奇偶校验码就具有校验这种差错的能力,它由两部分组成。
表1.2.4 8421奇偶校验码
 电子发烧友App
电子发烧友App




















评论