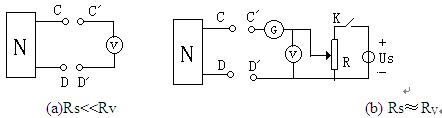
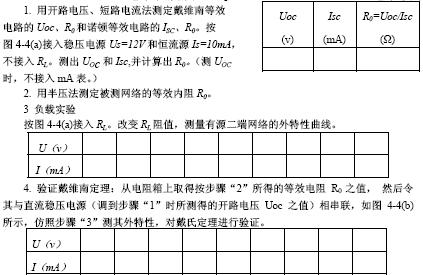
戴维南定理原理分析

戴维南定理原理分析

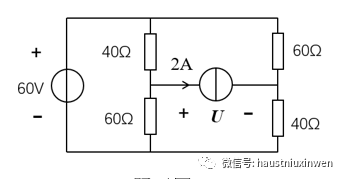
在电路计算中， 有时只需计算电路中某一支路的电流和电压， 如果使用支路电流法或叠加定理来分析， 会引出一些不必要的电流， 因此常使用戴维南定理来简化计算。
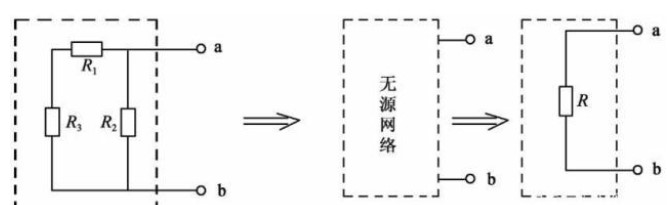
在讨论戴维南定理之前， 先介绍一下二端网络的概念。任何具有两个端点与外电路相连接的网络， 不管其内部结构如何， 都称为二端网络。

图2-5(a)、 (b)所示的两个网络都是已知电路结构的二端网络。 根据网络内部是否含有电源又分为有源二端网络和无源二端网络。 图2-5(a)是无源二端网络， 图2-5(b)是有源二端网络。 一般情况下， 有源二端网络可用一个带有字母A的方框加两个引出端表示， 无源二端网络可用一个带有字母P的方框加两个引出端表示， 有源二端网络与无源二端网络的连接方法如图2-5(c)表示。 很显然， 一个有源支路是最简单的有源二端网络， 一个无源支路是最简单的无源二端网络， 它们的连接如图2-5(d)所示。

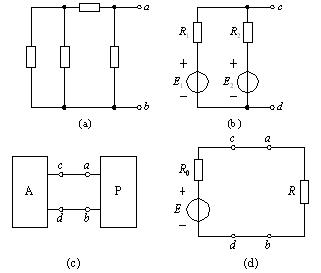
图2-5 二端网络的概念

任何一个无源线性二端网络， 其端电压与端点电流之间是符合欧姆定律的， 它们的比值是一个常数， 因此， 任何一个线性无源二端网络都可以用一个等效电阻来代替， 该等效电阻也称为无源二端网络的入端电阻。

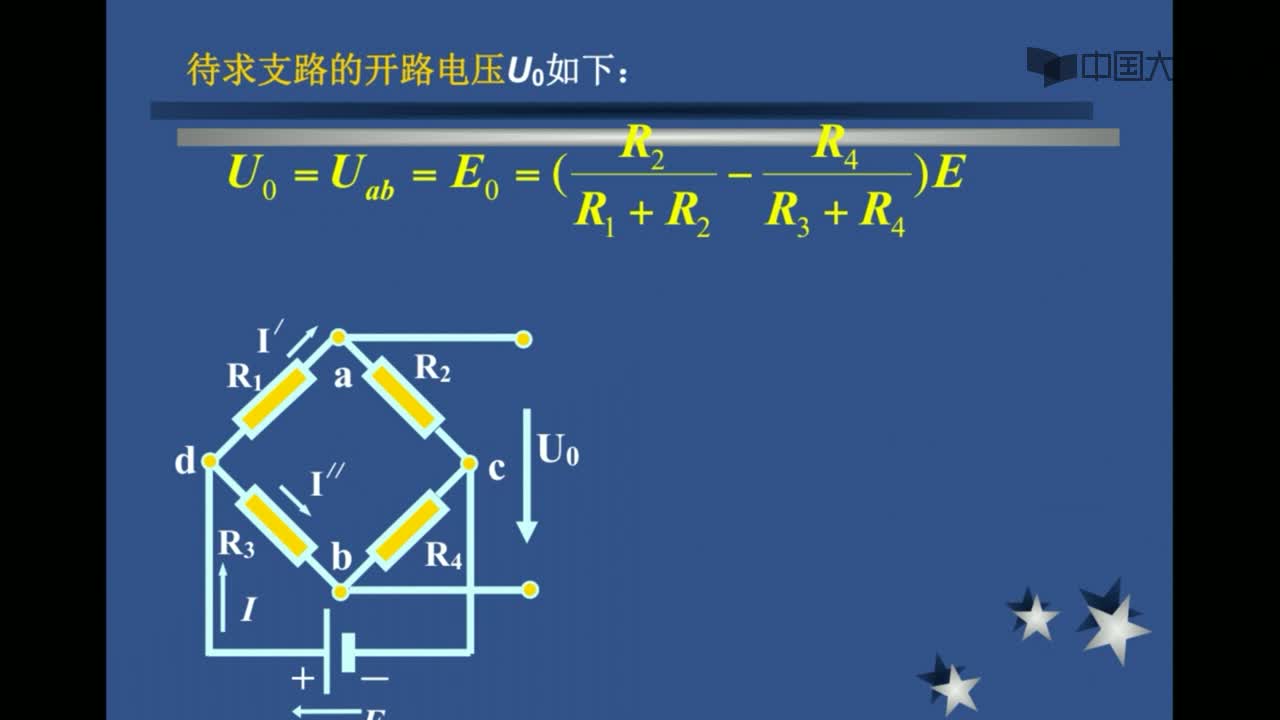
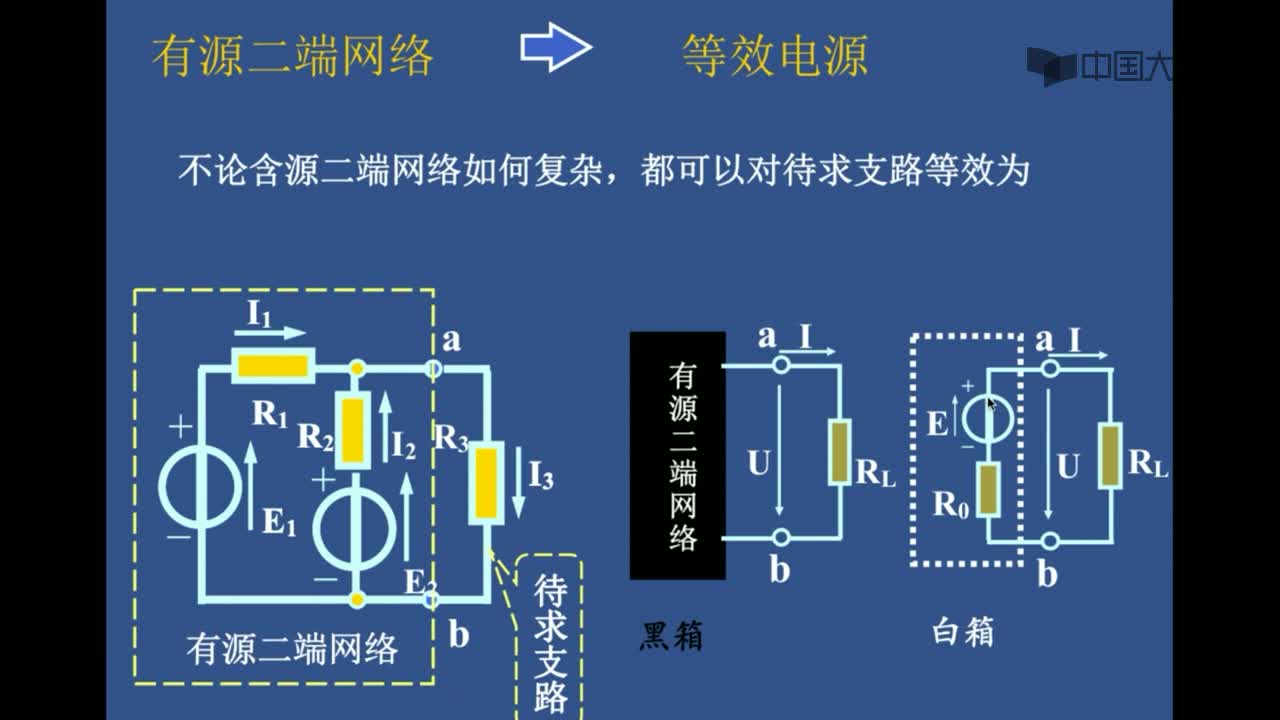
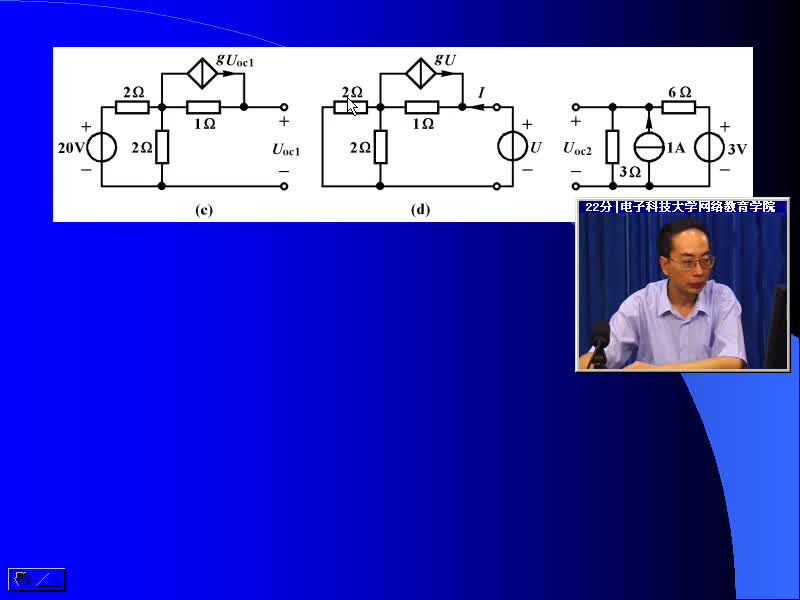
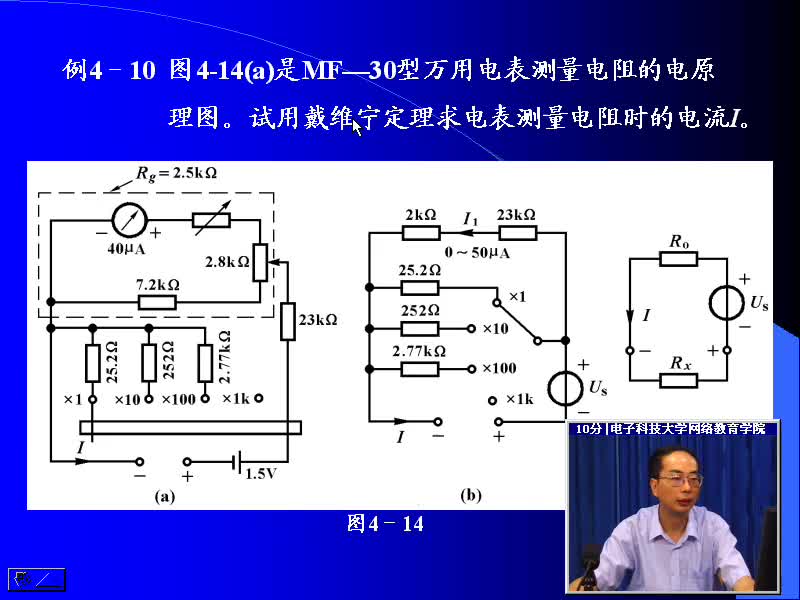
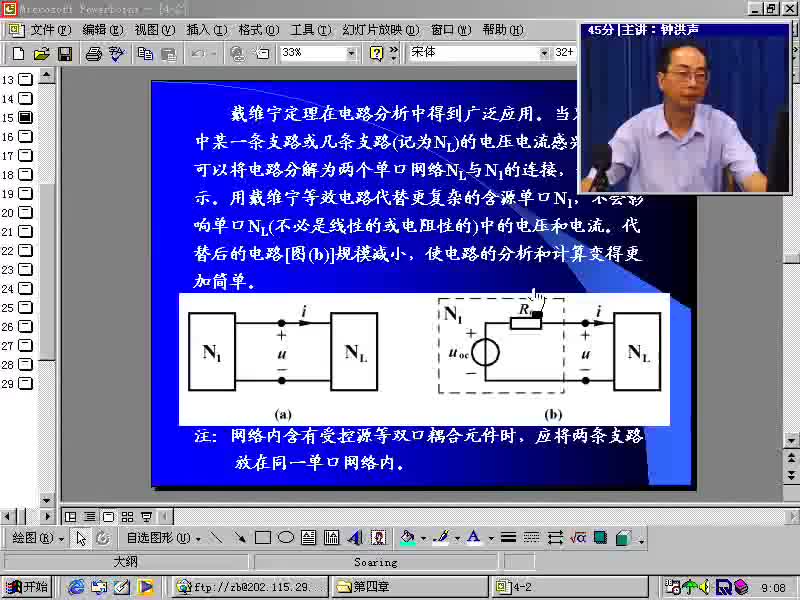
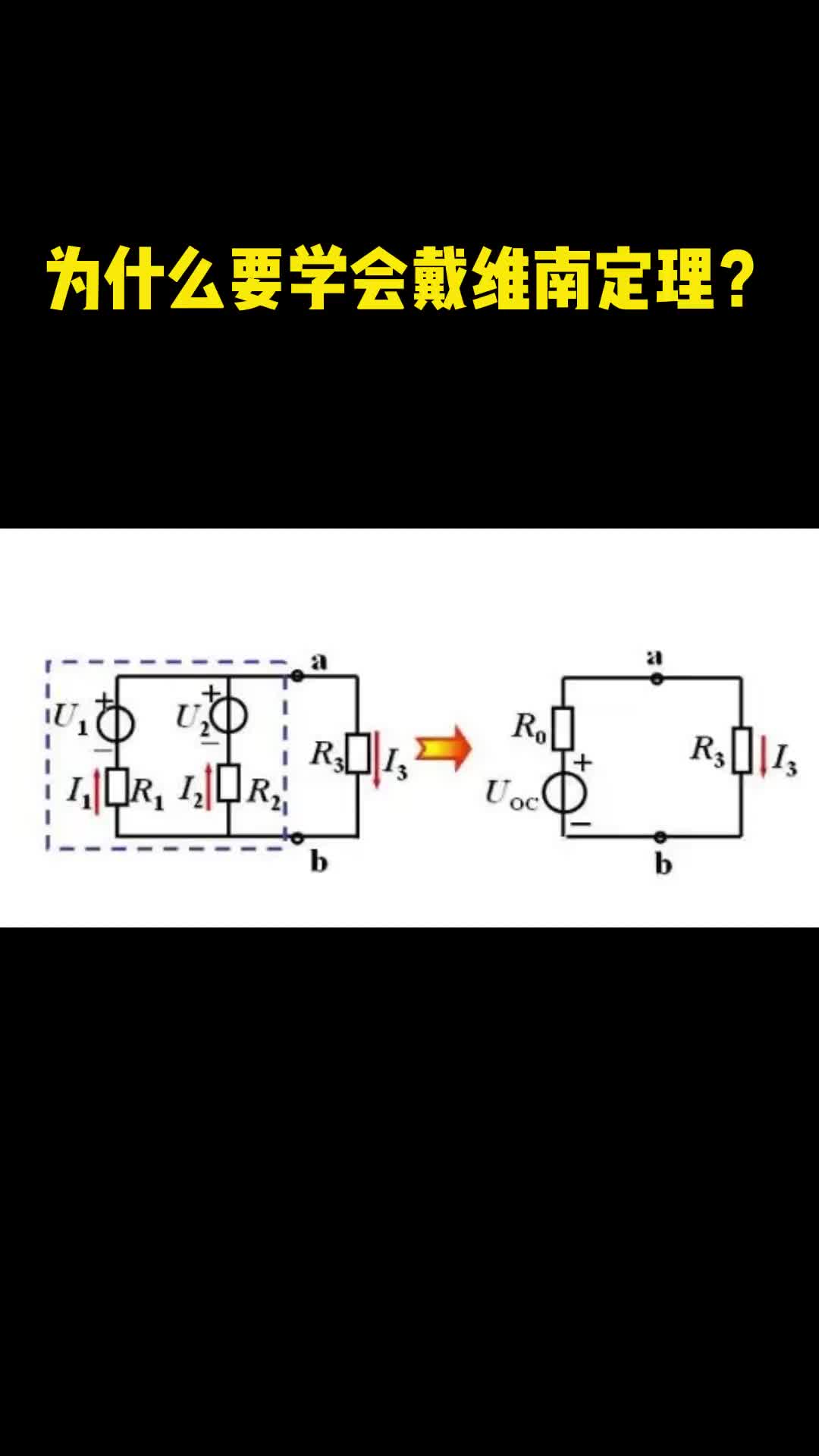
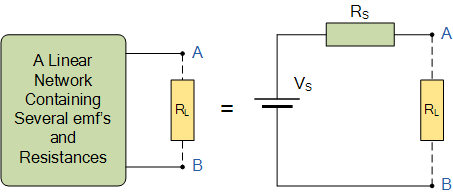
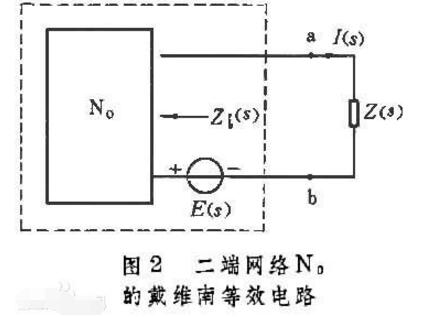
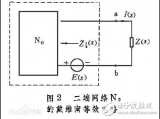
戴维南定理又称等效电压源定理。 可叙述如下： 任一线性有源二端网络， 对其外部电路来说， 都可用一个电动势为E的理想电压源和内阻R0相串联的有源支路来等效代替。 这个有源支路的理想电压源的电动势E等于网络的开路电压U0 ， 内阻R0 等于相应的无源二端网络的等效电阻。

所谓相应的无源二端网络的等效电阻， 就是原有源二端网络所有的理想电压源及理想电流源均除去后网络的入端电阻。 除去理想电压源， 即E=0， 理想电压源所在处短路； 除去理想电流源， 即Is=0， 理想电流源所在处开路。

详细请查看：电路的分析方法