01 基尔霍夫定理的内容是什么？ 基尔霍夫电流定律： 在电路任一节点，流入、流出该节点电流的代数和为零。 基尔霍夫电压定律： 在电路中的任一闭合电路，电压的代数和为零。 02 戴维南定理 一个含独立
2023-05-30 09:30:54
1994 
基尔霍夫定律包括基尔霍夫电流定律 （KCL）和基尔霍夫电压定律( KVL )。它反映了电路中所有支路电压和电流所遵循的基本规律，是分析集总参数电路的基本定律。基尔霍夫定律与元件特性构成了电路分析的基础。
2023-04-19 09:08:37
1 电路的基本定律有欧姆定律和基尔霍夫定律。
2023-03-22 16:05:461857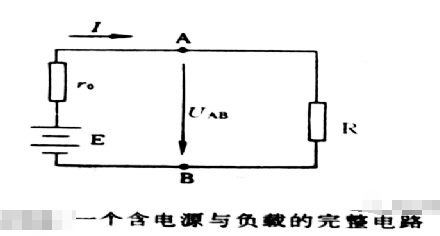 
、零状态响应。4、正弦稳态分析（18学时）正弦量及其相量表示 基尔霍夫定律的相量形式 元件伏安关系的相量形式 复阻抗与复导纳 正弦电路的分析计算 串并联谐振电路 交流电路的功率和复功率 简单有耦合电感
2008-11-25 15:12:37
以各模块计算具体的传递函数之前，在导出传递函数时，确认两个重要的定律。一个是指基尔霍夫的电流定律。本定律是指“任意的节点中电流的和为0”。本定律必须要注意的是电流的流向。另一个是指基尔霍夫的电压定律。
2023-02-24 09:51:14487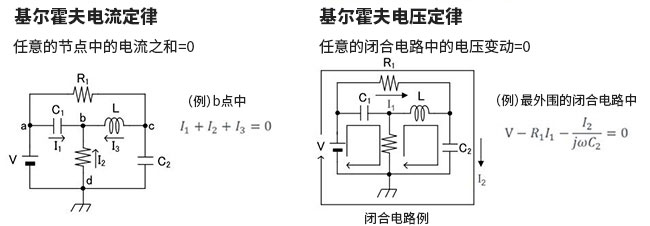 
基尔霍夫电流定律又被称为基尔霍夫第一定律（简称KCL）。它是应用于电路中的节点，所谓节点指的是电路中三个或两个以上的支路相连接的点。
2022-11-12 10:46:3541473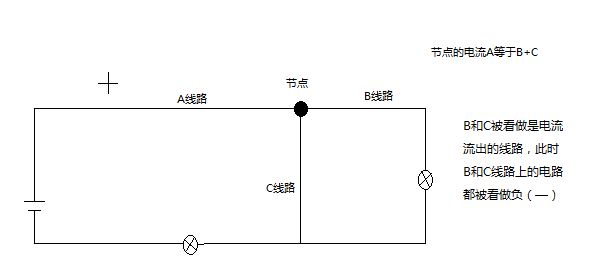 
基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上，在稳恒电流条件下严格成立。当基尔霍夫第一（基尔霍夫电流定律）、第二（基尔霍夫电压定律）方程组联合使用时，可正确迅速地计算出电路中各
2021-07-13 09:36:3318439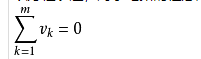 
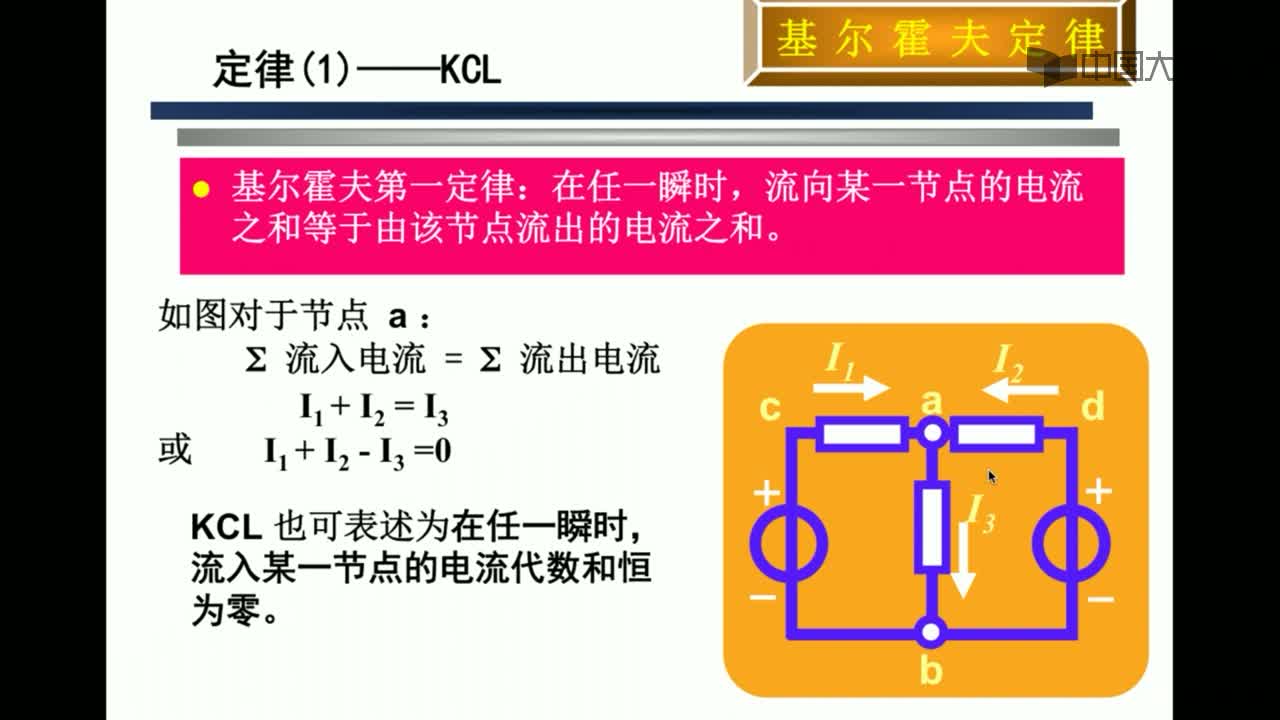
基尔霍夫第一定律又称节点电流定律。基尔霍夫第一定律的内容是：电路中任意节点电流的代数和等于零。在实际应用中，常规定流入节点的电流为正，流出节点的电流为负。这样，流入节点电流之和等于流出节点电流之和。
2021-05-15 17:32:4167025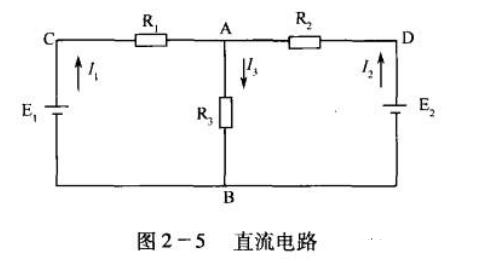 
基尔霍夫电流定律：在电路任一节点，流入、流出该节点电流的代数和为零。基尔霍夫电压定律：在电路中的任一闭合电路，电压的代数和为零。
2021-03-04 08:00:002 ，电子电路更加复杂。一根导体将分裂成多个分支，然后沿路径分裂成更多的迹线。但是，这些子电路最终在电源处合并为一个。 基尔霍夫的结定律与导体分支成多条路径或不同路径合并时电流的行为有关。路径分离或合并的点称为“
2020-12-15 17:00:091671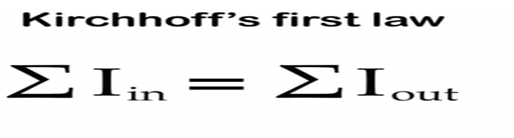 
基尔霍夫定律建立在电荷守恒定律、欧姆定律及电压环路定理的基础之上，在稳恒电流条件下严格成立。当基尔霍夫第一、第二方程组联合使用时，可正确迅速地计算出电路中各支路的电流值。由于似稳电流（低频交流电
2020-12-09 14:15:3214211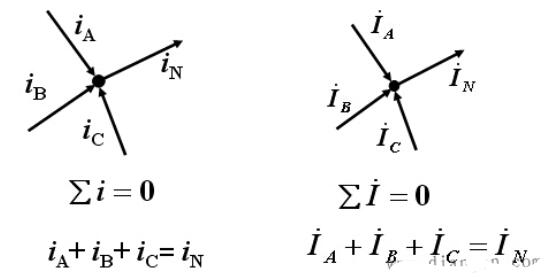 
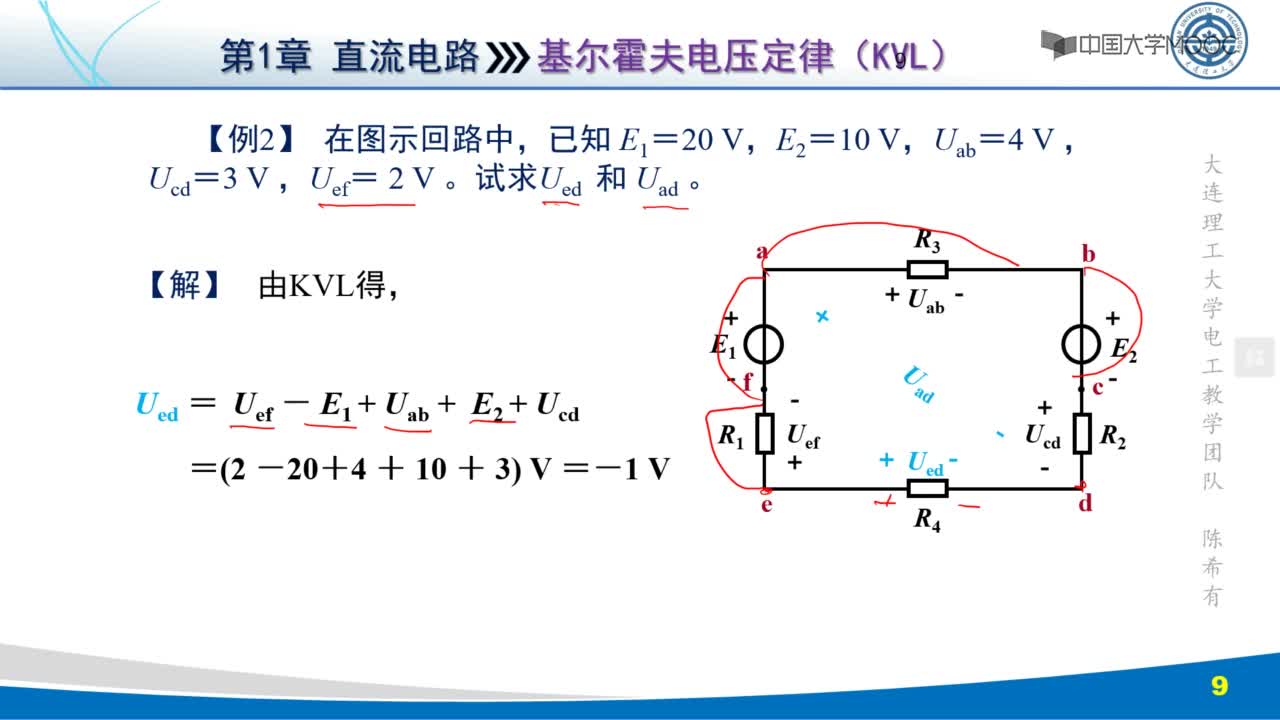
因此，在将基尔霍夫电压定律应用于特定电路元件时，重要的是我们要特别注意元件两端的电压降和源的电动势的代数符号（+和-），否则我们的计算可能是错误的。
2020-11-01 10:49:406428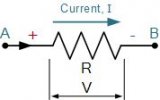 
Kirchhoffs定律之一是处理在闭合电路周围流动的电流，即Kirchhoffs电流定律（KCL），而另一条定律是处理闭合电路中存在的电压源，即Kirchhoffs Voltage法律（KVL）。 基尔霍夫斯
2020-10-22 11:22:539736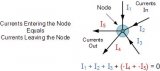 
一、实验目的1. 验证基尔霍夫定律的正确性，加深对基尔霍夫定律的理解。2. 学会用电流插头、插座测量各支路电流。
2019-09-11 17:02:4134 基尔霍夫的电流定律（KCL）是基尔霍夫的第一个定律，用于处理进入和离开结的电荷守恒。
2019-06-23 10:50:273567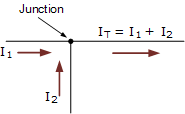 
给出了三个必备条件：两组方程的线形函数形式；确定方程组中每项正负号的法则；两组方程的独立方程个数。现在的基尔霍夫定律与原始的基尔霍夫定律并不完全相同，在某种程度上，它破坏了原始基尔霍夫定律所包含的三点的内容的统一，也破坏了原始基尔霍夫定律
2018-10-29 08:00:0016 本文分别对基尔霍夫电压和基尔霍夫电流定律进行了详细的介绍了。主要包括定律含义、内容、应用方法及例题等。
2018-07-20 15:48:4687088 基尔霍夫定律Kirchhoff laws是电路中电压和电流所遵循的基本规律，是分析和计算较为复杂电路的基础，1845年由德国物理学家G.R.基尔霍夫（Gustav Robert Kirchhoff
2017-12-20 16:03:5626036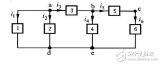 
基尔霍夫定律是求解复杂电路的电学基本定律。从19世纪40年代，由于电气技术发展的十分迅速，电路变得愈来愈复杂。某些电路呈现出网络形状，并且网络中还存在一些由3条或3条以上支路形成的交点（节点）。
2017-12-20 15:30:2632673 基尔霍夫定律Kirchhoff laws是电路中电压和电流所遵循的基本规律，是分析和计算较为复杂电路的基础，1845年由德国物理学家G.R.基尔霍夫（Gustav Robert Kirchhoff
2017-10-31 08:46:06122936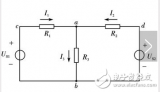 
基尔霍夫第一定律为基尔霍夫电流定律，第二定律为基尔霍夫电压定律。
2017-08-15 19:51:23134821 1845年，刚从德国哥尼斯堡大学毕业、年仅21对的基尔霍夫在他的第一篇论文中提出了适用于网络状电路计算的两个定律，即著名的基尔霍夫定律。这两个定律分为基尔霍夫第一定律和基尔霍夫第二定律，其中基尔霍夫第一定律称为基尔霍夫电流定律，简称KCL；基尔霍夫第二定律即为基尔霍夫电压定律，简称KVL。
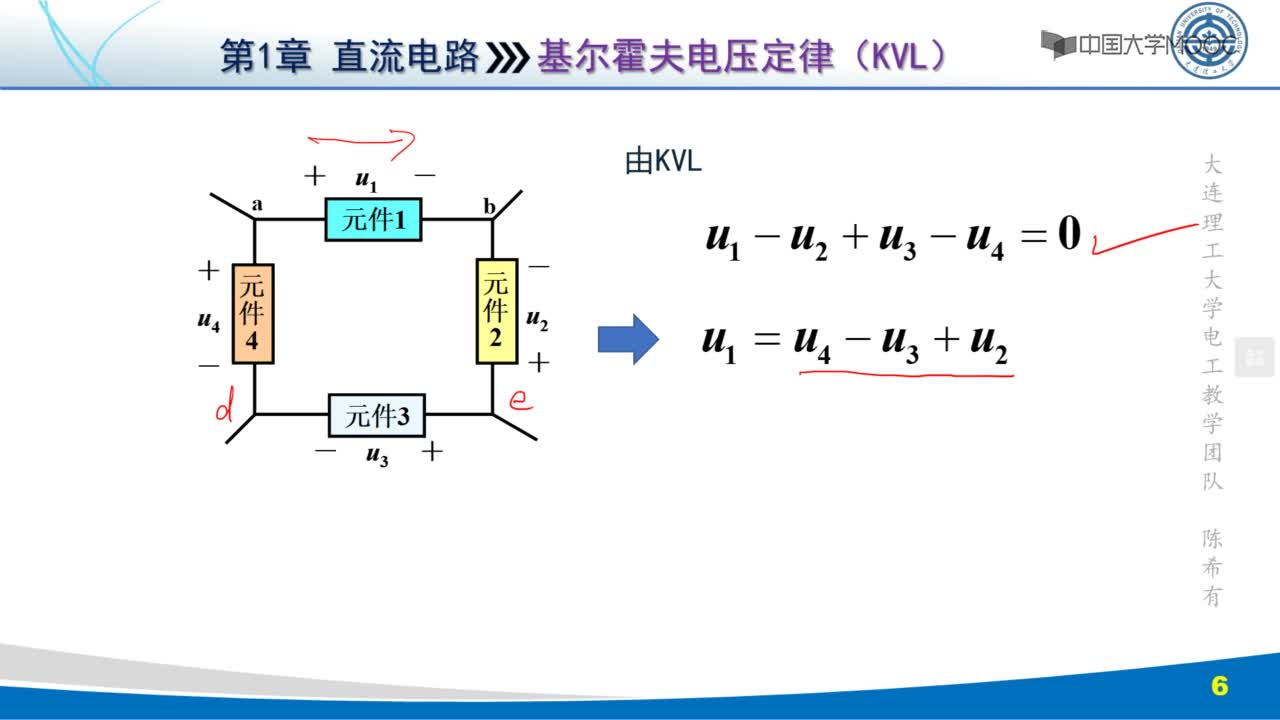
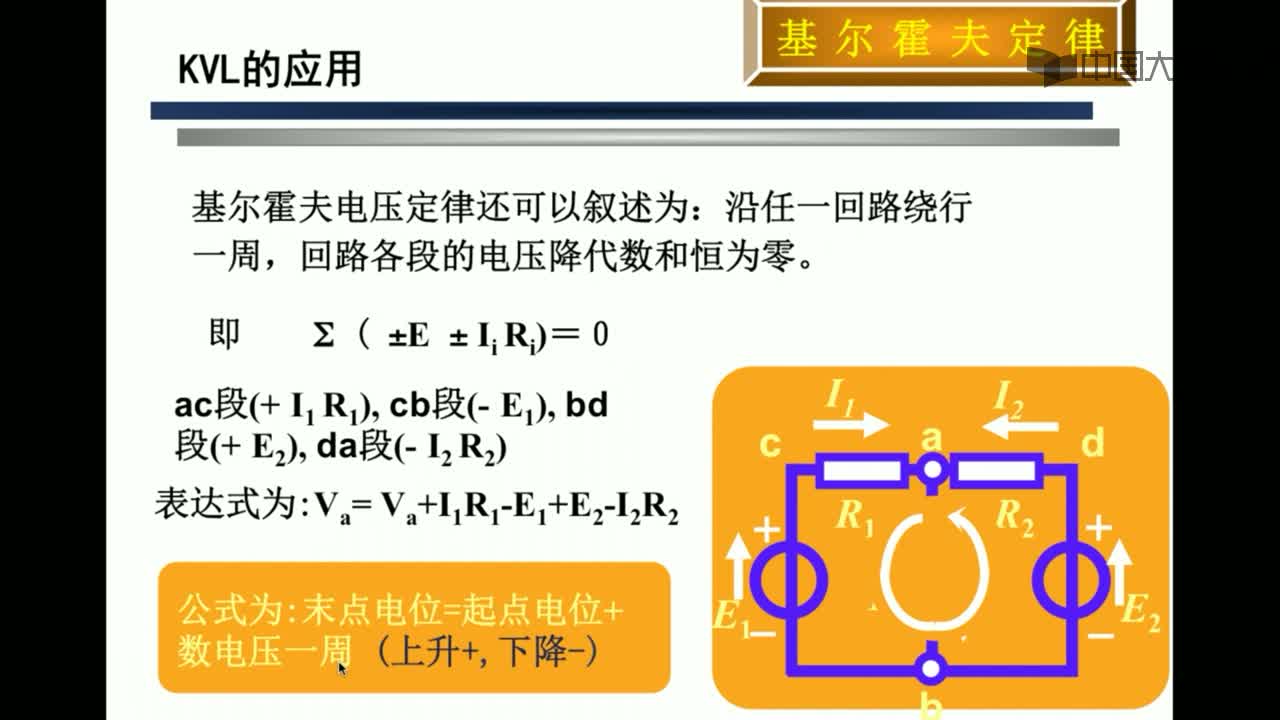
2017-08-15 17:37:00234389 基尔霍夫电压定律（Kirchhoff laws）是电路中电压所遵循的基本规律，是分析和计算较为复杂电路的基础，内容是，在任何一个闭合回路中，各元件上的电压降的代数和等于电动势的代数和，即从一点出发绕回路一周回到该点时，各段电压的代数和恒等于零，即∑U=0
2017-08-15 17:09:2331285 基尔霍夫电流定律也称为节点电流定律，于1845年由德国物理学家G.R.基尔霍夫（Gustav Robert Kirchhoff，1824～1887）提出，内容是电路中任一个节点上，在任一时刻，流入节点的电流之和等于流出节点的电流之和。
2017-08-15 16:56:4921538 
KCL定律的仿真和KVL定律的仿真
2011-07-24 00:29:023624 
基尔霍夫定律
基尔霍夫定律是描述电路中电压、电流遵循的最基本的规律。在介绍基尔霍夫定律之前，首先
2009-07-27 10:15:4610679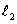 
热辐射基本定律和辐射特性:热辐射应用背景,实际物体吸收比与基尔霍夫定律,固体和液体的辐射特性,黑体辐射基本定律,热辐射的基本概念
2009-07-06 07:19:0324 电位、基尔霍夫定律和 叠加原理实验目的：1. 验证电路中电位的相对性、电压的绝对性。2. 验证基尔霍夫定律的正确性，加深对基尔霍夫定律的理解。3 .验证线性电路叠
2009-03-23 16:22:0622 基尔霍夫定律及叠加原理的验证
一、实验目的1 ．熟悉实验台的布局及直流电压源、直流电 压表电流表的使用方法。
2009-03-18 20:49:1522324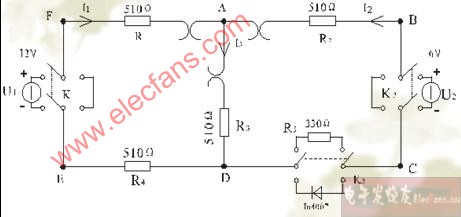 
实验 基尔霍夫定律与叠加原理一． 实验目的
1. 验证基尔霍夫定律的正确性，加深对基尔霍夫定律的理解。
2008-11-02 22:20:5014977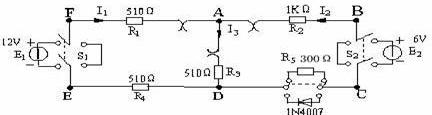 
基尔霍夫定律的基本内容是什么?基尔霍夫定律是电路分析和计算的重要工具。依据它可以作出决定电路特性的电流方程式和电压方程式。基尔霍夫定律又分为第
2008-10-04 15:08:118898 
基尔霍夫定律实验
一、实验目的?⒈ 验证基尔霍夫定律。?
2008-09-24 19:17:4136324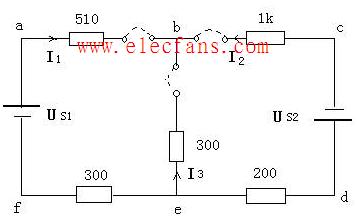 
验证基尔霍夫定律
一、实验目的1. 验证基尔霍夫定律的正确性，加深对基尔霍夫定律的理解。2. 学会用电流
2008-09-24 09:28:2317079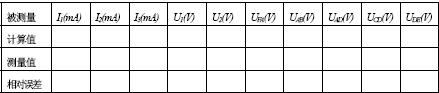 
基尔霍夫定律的验证
一．实验目的1．验证基尔霍夫定律，加深对基尔霍夫定律的理解；2．掌握直流电流表的使用以及学会用电流插头、
2008-09-22 15:27:0038061
电工实验指导书一、功率因数及相序的测量53二、基尔霍夫定律的验证8三、叠加原理的验证10
2008-09-22 14:38:3951
正在加载...
电子发烧友App
（3-7-1）
（3-7-2）
（3-7-3）
（3-7-4）
，
，求
的值。
得：
，图3-7-1b中画出了电压的相量图。
工商网监
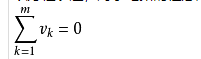
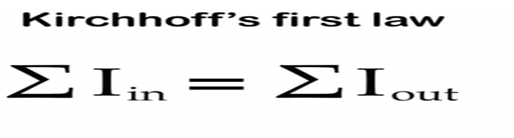
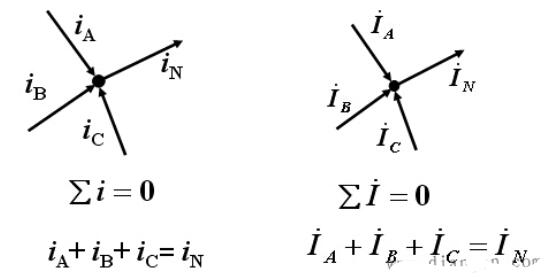
评论