正弦交流电路的功率计算
如果一端口网络的端口电压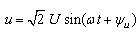
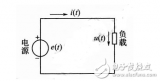
 ,且电压与电流参考方向一致,如图3-9-1a所示。则由功率定义可得输入该一端口网络的瞬时功率为:
,且电压与电流参考方向一致,如图3-9-1a所示。则由功率定义可得输入该一端口网络的瞬时功率为:
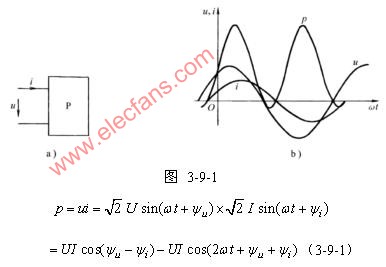
由式可看出,瞬时功率可分为恒定分量 与二倍角频率变化的正弦分量
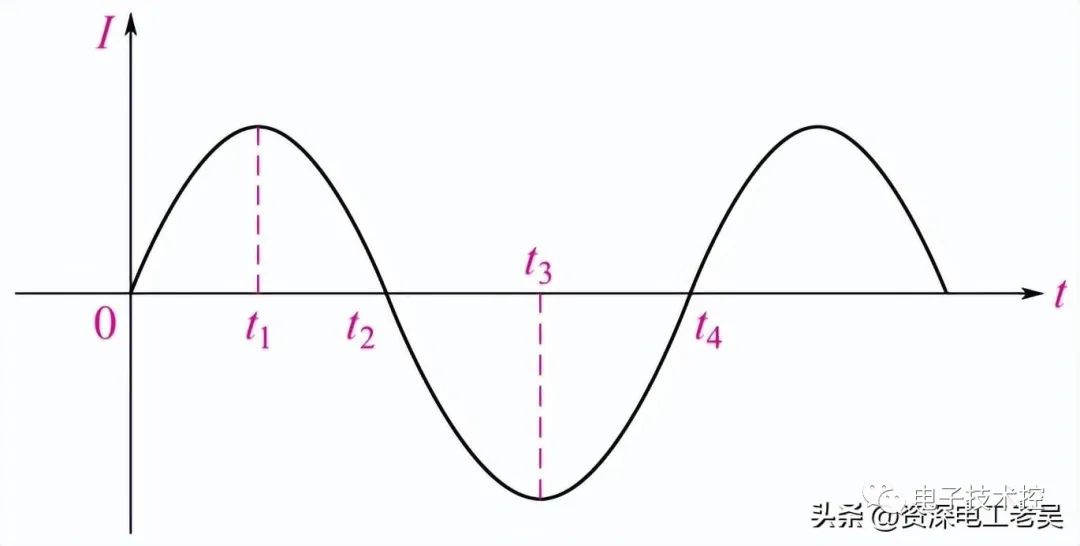
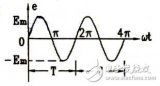
与二倍角频率变化的正弦分量 。图3-9-1b为端口电压u、端口电流i与瞬时功率p的波形图。瞬时功率在某些时间段为正值,表示此时一端口网络正在吸收功率。在某些时间段为负值,表示网络在输出功率,将原来储存的能量送回电网。
。图3-9-1b为端口电压u、端口电流i与瞬时功率p的波形图。瞬时功率在某些时间段为正值,表示此时一端口网络正在吸收功率。在某些时间段为负值,表示网络在输出功率,将原来储存的能量送回电网。
在一周期内电路吸收的平均功率,也称为有功功率。它的值为
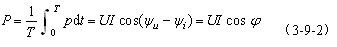
式中,U、I为负载端电压和电流的有效值;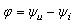 是端电压与电流在关联参考方向下的相位差;
是端电压与电流在关联参考方向下的相位差; 称作功率因数角。由式可看出,决定一个一端口网络负载平均功率的大小,不但与施加的电压,流过的电流的有效值大小有关,而且与电压电流的相位差,即功率因数角
称作功率因数角。由式可看出,决定一个一端口网络负载平均功率的大小,不但与施加的电压,流过的电流的有效值大小有关,而且与电压电流的相位差,即功率因数角 有关。当电压电流相位差接近
有关。当电压电流相位差接近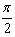 时,即使U与I的乘积很大,但负载所吸收的功率仍然很小,这是因为负载的功率因数
时,即使U与I的乘积很大,但负载所吸收的功率仍然很小,这是因为负载的功率因数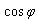 很小。例如对于纯电感(或纯电容)的负载,电压与电流互相正交,
很小。例如对于纯电感(或纯电容)的负载,电压与电流互相正交,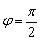 ,
,![]()
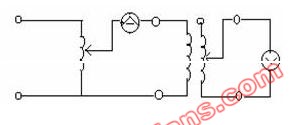
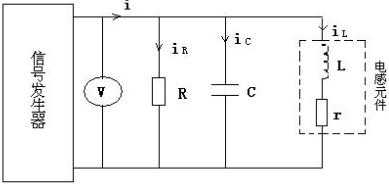
测量一端口网络的功率时,电路连接如图3-9-2b所示。将电流线圈串入被测量的电路,电压线圈与端口并联。二组线圈中分别流过电流,并产生磁场。功率表的读数等于加在电压线圈上的电压有效值和通过电流线圈的电流有效值的乘积,再乘以电压相量(参考方向从星号指向非星号)和电流相量(参考方

向也从星号指向非星号)之间的相位差的余弦,即 。若在测量同一负载功率时,功率表的连接方式改为如图3-9-2c所示,此时流过电流线圈(参考方向为从非星号指向星号)的电流相量相位与原来接法相差180度,因此瓦特表的读数为
。若在测量同一负载功率时,功率表的连接方式改为如图3-9-2c所示,此时流过电流线圈(参考方向为从非星号指向星号)的电流相量相位与原来接法相差180度,因此瓦特表的读数为 ,即读数为负值。
,即读数为负值。
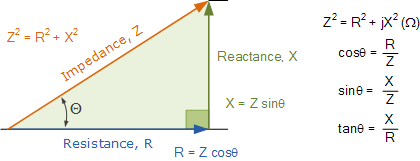
有功功率、无功功率和视在功率的关系为

由上面各式可看出,视在功率、有功功率和无功功率组成一个直角三角形。
在电力系统的计算中,为了使功率计算表达方便,常在正弦电路中用复数功率来表示一个元件或一个单端口网络的功率。复数功率定义为 的乘积,用符号
的乘积,用符号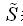 来表示,即:
来表示,即:
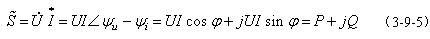
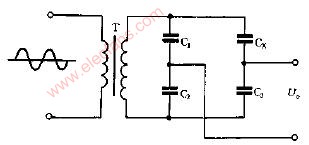
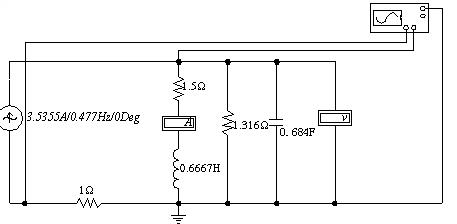
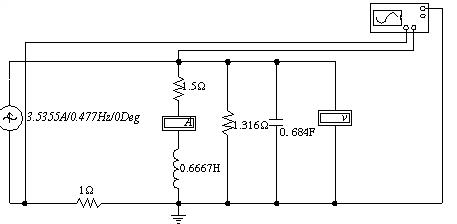
例3-9-1 图3-9-3所示电路,已知 ,求输入该电路的有功功率、无功功率和视在功率。
,求输入该电路的有功功率、无功功率和视在功率。


解:电感线圈可表示成电阻与电感的串联电路,由已知测量数据可得电阻值为
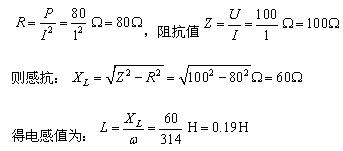
 电子发烧友App
电子发烧友App








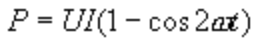
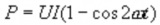


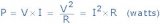
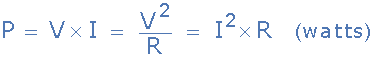
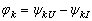
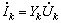
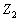
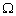
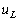
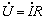
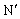
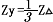












评论