本节讨论长线方程的正弦稳态解的物理含义。从式(10-3-6)知,电压![]() 由两项组成,第一项为
由两项组成,第一项为![]() (设
(设![]() ),将它写成时间函数,记为
),将它写成时间函数,记为 ,则:
,则:
![]() (10-4-1)
(10-4-1)
 是时间t和距离x的函数,可写成
是时间t和距离x的函数,可写成![]() 。先固定某一地点,设
。先固定某一地点,设![]() ,则:
,则:
![]() (10-4-2)
(10-4-2)
式中,![]() 是正弦函数的振幅,
是正弦函数的振幅,![]() 是正弦函数的初相。可见在某点
是正弦函数的初相。可见在某点 的
的 是随时间而变的等幅正弦振荡。如图10-4-1所示。
是随时间而变的等幅正弦振荡。如图10-4-1所示。
再固定某一时间![]() ,则:
,则:
![]() (10-4-3)
(10-4-3)
它是随距离x变化的正弦衰减振荡,振幅为![]() 。
。
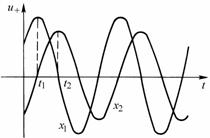
图10-4-1
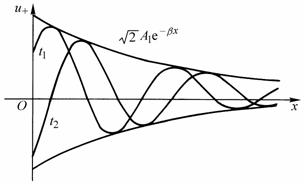
图10-4-2
![]() 和
和![]() 两个瞬时
两个瞬时 沿线分布曲线如图10-4-2所示。它们是以
沿线分布曲线如图10-4-2所示。它们是以![]() 为包络线的衰减正弦曲线。
为包络线的衰减正弦曲线。
综上所述, 是随着时间的增大沿x增大方向推进,并在推进方向逐渐衰减的行波。这种自电源向负载方向推进的行波称为正向行波。
是随着时间的增大沿x增大方向推进,并在推进方向逐渐衰减的行波。这种自电源向负载方向推进的行波称为正向行波。
行波的推进速度是用相位保持不变的点的移动速度来表示的,称为相位速度,可由下式计算:
![]() (10-4-4)
(10-4-4)
对于架空传输线,相位速度是真空中的光速,即![]() 。
。
行波在一个周期行进的距离称为波长 ,于是:
,于是:
![]() (10-4-5)
(10-4-5)
式(10-3-6)中电压![]() 的第二项为
的第二项为![]() (设
(设![]() ),对应的时间函数记为
),对应的时间函数记为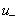 :
:
![]() (10-4-6)
(10-4-6)
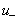 是沿x减少的方向以相速
是沿x减少的方向以相速![]() 传播的衰减波,即由终端沿线向始端传播的衰减正弦波,称为反向行波。
传播的衰减波,即由终端沿线向始端传播的衰减正弦波,称为反向行波。
同样,也可将式(10-3-7)中的电流I分解为电流直波和电流回波,即:
![]() (10-4-7)
(10-4-7)
现在解释特性阻抗的含义。从式(10-4-6)和式(10-4-7)可知:
![]() (10-4-8)
(10-4-8)
即特性阻抗![]() 是入射电压对入射电流之比,
是入射电压对入射电流之比,![]() 也称为波阻抗。
也称为波阻抗。
将电压、电流写成瞬时函数表达式:
 (10-4-9)
(10-4-9)
 (10-4-10)
(10-4-10)
式中:![]() 。
。
沿传输线任一点,反射电压(或反射电流)对入射电压(或入射电流)之比,称为反射系数N,可以证明:
![]() (10-4-11)
(10-4-11)
式中:![]() 是始端输入阻抗。
是始端输入阻抗。
N的另一表达式为:
![]() (10-4-12)
(10-4-12)
在终端上:
![]() (10-4-13)
(10-4-13)
式中:![]() 是终端负载阻抗。
是终端负载阻抗。
 电子发烧友App
电子发烧友App










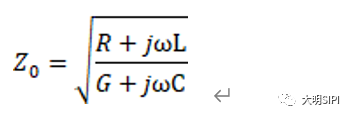






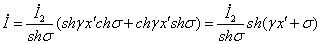











评论