2.4 二极管基本电路及其分析方法
2.4.1 二极管正向V-I模型
一、理想模型
理想二极管的V–I 特性如图(a)蓝色线所示,虚线表示实际二极管的V–I 特性。图(b)为它的代表符号。
二极管的理想模型
由图(a)可见,在正向偏置时,其管压降为0V,而当二极管处于反向偏置时,认为它的电阻为无穷大,电流为零。在实际的电路中,当电源电压远比二极管的管压降大时,利用此法来近似分析是可行的。
 二极管的恒压降模型
二极管的恒压降模型
二、二极管的恒压降模型
二极管的恒压降模型
二极管的恒压降模型及代表符号如图所示。该模型建立的基本思想是当二极管导通后,其管压降可认为是恒定的,不随电流而变,且导通电压的典型值为0.7V(硅管)。此模型只有当二极管的电流 iD近似等于或大于1mA时才是正确的。该模型提供了一种合理的近似,因此应用也较广。 二极管的恒压降模型
二极管的恒压降模型
三、二极管的折线模型
二极管的折线模型
为了较真实地描述二极管V-I 特性,二极管折线模型,在恒压降模型的基础上,作一定的修正,即认为二极管的管压降不是恒定的,而是随着通过二极管电流的增加而增加。所以,在模型中用一个电池和一个电阻rD来作进一步的近似。
二极管折线模型如图(a)所示。这个电池的电压选定为二极管的门坎电压Vth,约为0.5V(硅管)。至于rD的值,可以这样来确定,即当二极管的导通电流为1mA时,管压降为0.7V,于是rD的值可计算如下:
由于二极管特性的分散性,Vth和rD的值不是固定不变的。
四、二极管的小信号模型

二极管小信号模型如图(b)所示。如果二极管在图(a)中的静态工作点Q(vD=VD,iD=ID)附近工作,则可把V-I 特性看成为一条直线,其斜率的倒数就是所要求的小信号模型的微变电阻rd,
rd=dvD/diD
rd的数值可从二极管的V-I 特性表达式导出:
(1)
取iD对vD的微分,可得微变电导
由此可得
(当T=300K时)
例如,当Q点上的ID=2mA时,rd=26mV/2mV=13W。
2.4.2 模型分析法应用举例
一、静态工作情况分析

例1 设二极管电路如图(a)所示,R =10kW,图(b)是它的习惯画法。对于下列两种情况,求电路的ID和VD的值:(要求在每种情况下,分别应用理想模型、恒压降模型和折线模型求解)
(1)VDD=10V;
(2)VDD=1V。
解:(1)VDD=10V
① 使用理想模型图(c)得
VD=0V,ID=VDD/R =10V/10kW=1mA
② 使用恒压降模型图(d)得
,
③ 使用折线模型图(e)得
VD=0.5V+IDrD=0.5V+0.931mA×0.2kW=0.69V
(2) VDD=1V
① 使用理想模型得
,
② 使用恒压降模型得
,
③ 使用折线模型得 ID=0.049 mA VD=0.51V
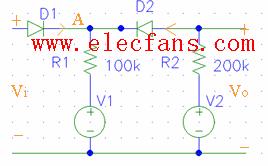
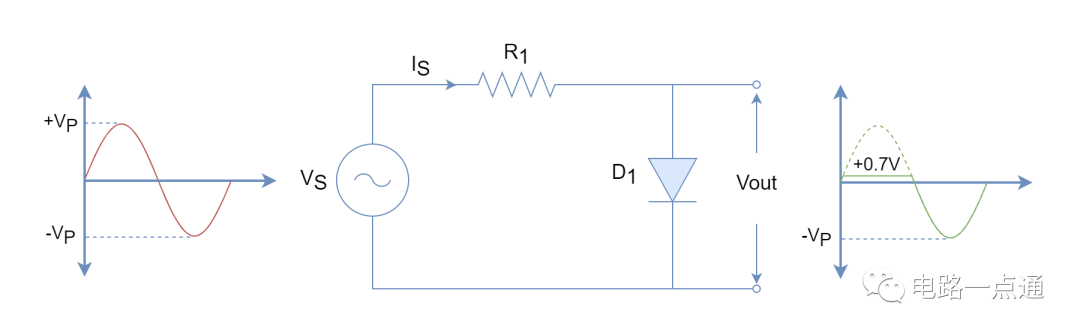
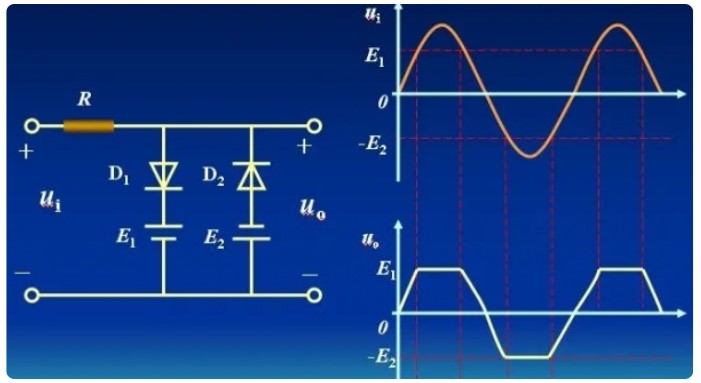
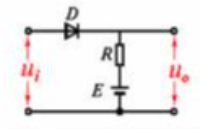
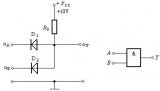
二、限幅电路分析
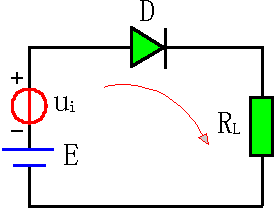
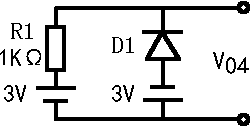
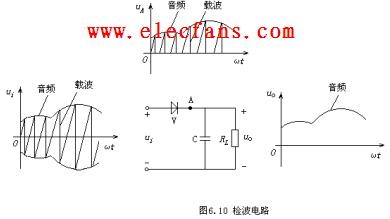
一种简单的限幅电路如图所示。当vI小于二极管导通电压时,二极管不导通,vO » vI;当vI超过二极管的导通电压vD,二极管导通,其两端电压就是vD。由于二极管正向导通后,其两端电压变化很小,所以当vI有很大变化时,vO的值却被限制在一定范围内。这种电路可用来减少某些信号的幅值,以适应不同的要求或保护电路中的元器件。

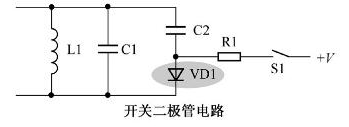
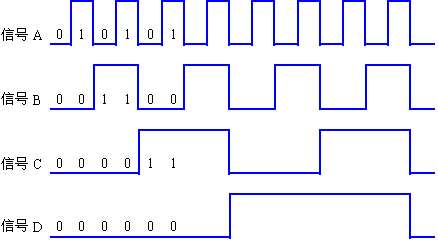
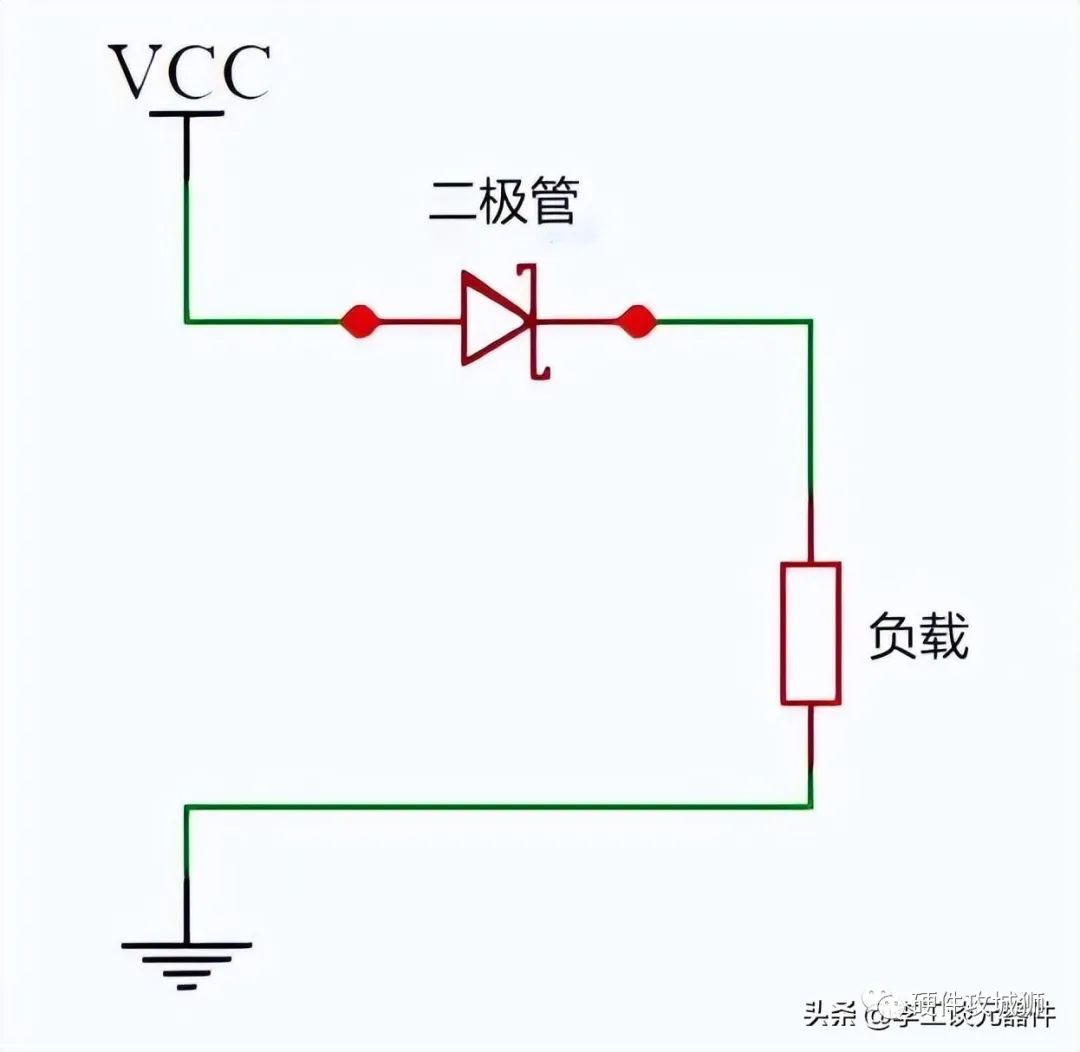
三、开关电路分析

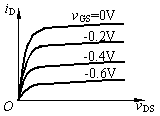
二极管的伏安特性
从二极管的伏安特性分析可以知道,当其两端电压低于导通电压时,二极管不导通,相当于开关断开;当其两端电压超过导通电压时,二极管导通,相当于开关接通。所以,二极管的实际作用很象一个开关,只是这个开关不够理想,开关接通时其导通压降不为零。此开关特性在数字电路是得到广泛的应用。
要判断电路中二极管处于导通状态还是截止状态,应当掌握的基本方法是:可以先将二极管断开,然后计算二极管两端的电位,若是外加的是正向电压则二极管导通,否则二极管截止。
 电子发烧友App
电子发烧友App









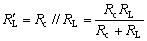
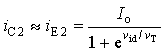
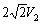
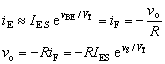
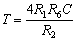













评论