数制与进位记数法
在采用进位记数的数字系统中, 如果只用r个基本符号 (例如0,1,2,…r-1) 、通过排列起来的符号串表示数值,则称其为基r数制(Radix-r Number System), r称为该数制的基(Radix)。假定用m+k个自左向右排列的符号Di(-k≤i≤m-1)表示数值N,即
N = Dm-1 Dm-2 … D1 D0 D-1 D-2 …D-k (2.1)
式中的Di(-k≤i≤m-1)为该数制采用的基本符号,可取值0、1、2、…、r-1,小数点位置隐含在 D0与D-1位之间, 则Dm-1 … D0 为N的整数部分,D-1 … D-n 为N的小数部分。
如果每个 Di 的单位值都赋以固定的值Wi ,则称Wi 为该位的权 (Weight) , 此时的数制称为有权的基r数制(Weighted Radix-r Number System)。此时N代表的实际值可表示为:
m-1
N = ∑ Di * Wi (2.2)
i= -k
如果该数制编码还符合 "逢r进位"的规则, 则每位的权(简称位权)可表示为:
Wi = ri
式中的r是数制的基,i为位序号。式 (2.2) 又可以写为:
m-1
N = ∑ Di * ri (2.3)
i = -k
式中的符号:
r 是这个数制的基(Radix)
i 表示这些符号的排列次序,即位序号
Di 是位序号为i的一位上的符号
ri 是第i位上的一个1所代表的值(位权)
Di * ri 是第i位上的符号所代表的实际值
∑ 表示对m+k位的各位的值执行累加求和
N 代表一个数值
此时该数制被称为r进位数制 (Positional Radix-r Number System), 简称r进制。下面是计算机中常用的几种进位数制:
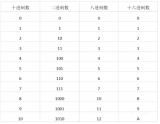
二进制 r=2, 基本符号 0,1
八进制 r=8, 基本符号 0,1,2,3,4,5,6,7
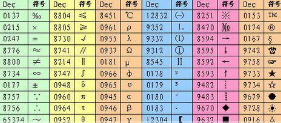
十六进制 r=16, 基本符号 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
其中A-F分别表示十进制数10,11,12,13,14,15
十进制 r=10, 基本符号 0,1,2,3,4,5,6,7,8,9
如果每一数位都具有相同的基, 即采用同样的基本符号集来表示, 则称该数制为固定基数值 (Fixed Radix Number System),这是计算机内普遍采用的方案。在个别应用中, 也允许对不同的数位或位段选用不同的基,即混合采用不同的基本符号集来表示, 则该数制称为混合基数制 (Mixed Radix Number System)。
 电子发烧友App
电子发烧友App














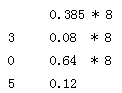

















评论