比较器的原理及应用

本文详细介绍比较器的应用场合、原理及类型。从2005年到2006年，比较器的市场增长已超过了20%，但比较器在放大器整体市场中所占的份额仅为10%。

　　查阅维基百科便会发现大家熟知的双路/四路比较器LM393/LM339排名很靠前。事实上，这两个比较器也是现今业内使用最为普遍的器件系列之一。原因为何？如果单从经济角度考虑，运算放大器也可用作比较器，但这样的做法是否可行？比较器的关键特性是什么？这些特性对于什么样的应用最重要？

　　本文将解答上述疑问，并结合应用实例，说明如何利用比较器实现高性能电路的设计。

　　什么是比较器？它和放大器有什么不同？

　　我们从工程学教程里了解到，运算放大器需要三个内部级才能发挥出最佳性能，比如实现高输入阻抗、低输出阻抗和高增益等。三个内部级分别是差分输入级、增益级（有或没有内部频率补偿）和输出级。这种基本的体系结构已经沿用了好几十年。早期，运算放大器曾作为数学运算的基本器件，主要以电压和电压信号来作标识。在反馈应用中，通过配置放大器周边的无源或有源器件，可以令系统执行加、减、乘、除和对数等运算。

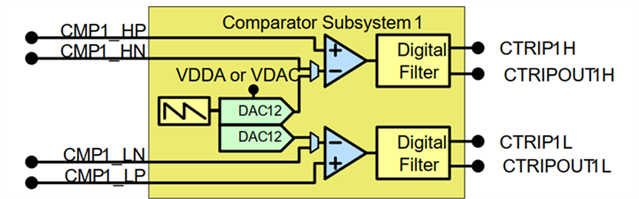
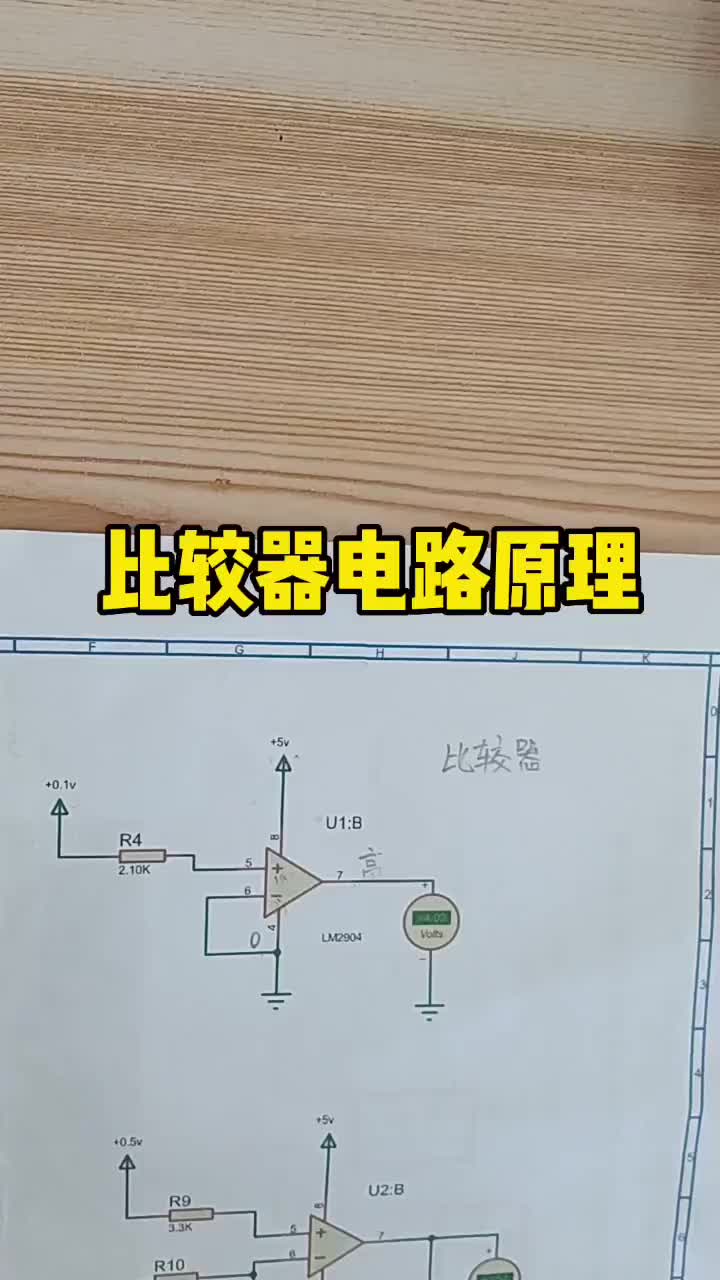
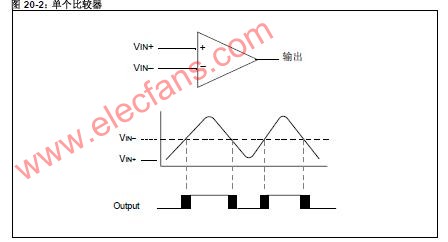
　　比较器其实可看成一个能够作逻辑 “决策”的逻辑输出电路。换句话说，它可把输入信号与已定义的参考电平进行比较。比较器的逻辑输出功能可以帮助用户设计具有多样化的额外功能的模拟电路。而且，无论是高速ADC、SAR型ADC还是Sigma-Delta ADC，比较器都是组建集成ADC的内部基本而又关键的模块。

　　在LM339的数据表中，列出了大量的应用。这基本上可以解释其在过去30年中为何被业界广泛地采用。以下列出LM339的一些常见应用：

　　·逻辑电平平移；

　　·过零检测/触发电路；

　　·电压信号/电源电压监察；

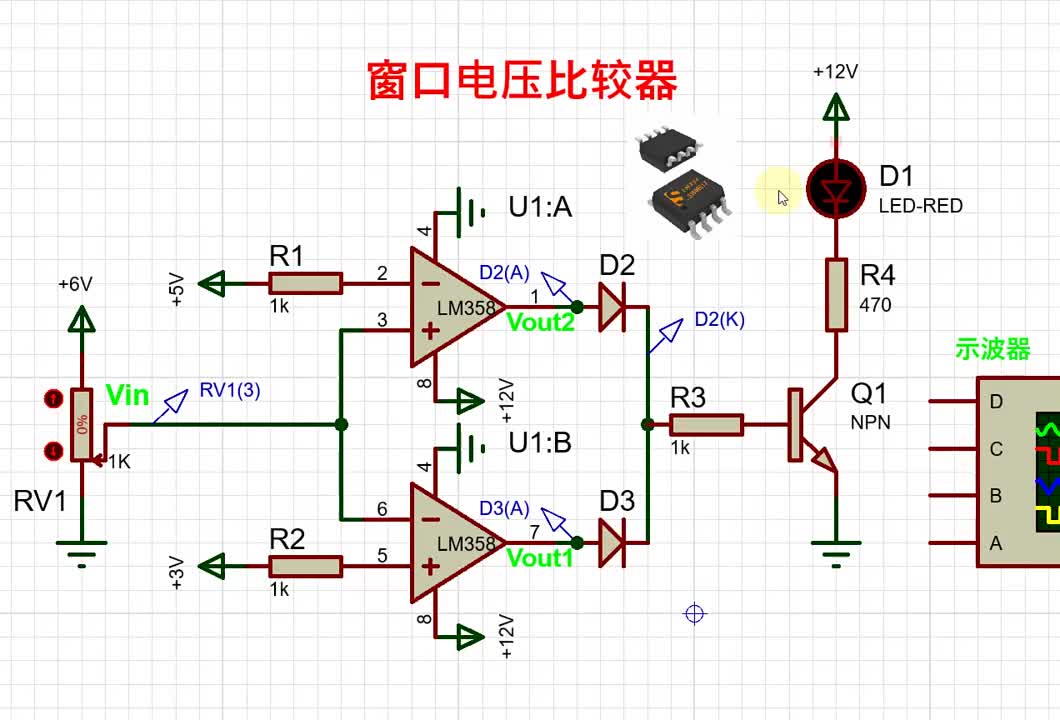
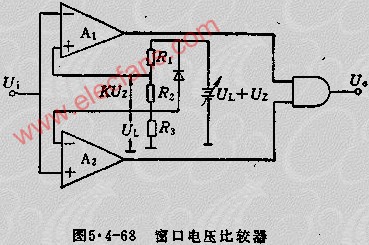
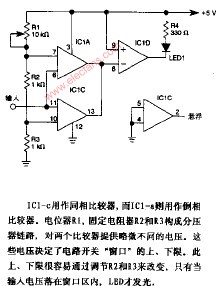
　　·Window比较器、施密特触发器；

　　·振荡器；

　　·时钟缓冲器；

　　·互导放大器。

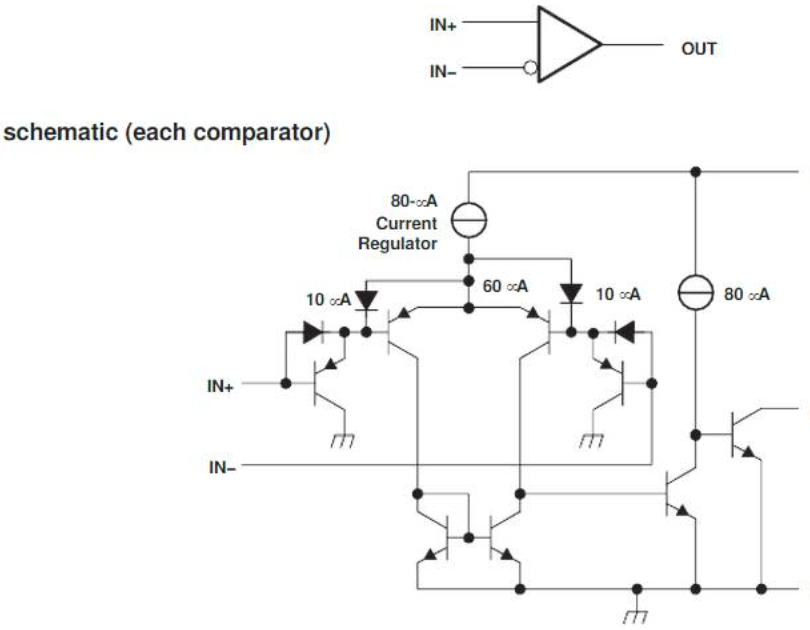
　　比较器的基本体系结构和大部份的参数属性都与运算放大器类似。因此，运算放大器也可充当比较器。但放大器并不是专门针对比较功能而开发的，而且放大器的数据表一般都不保证这项功能可否正常实现。运算放大器与比较器的最大分别在于比较器是开环设计，没有反馈环节，而且输出会在任何一条电源轨的范围内显示差分输入信号的极性。

　　此外，比较器一般都会被设计成 “过压驱动”（overdriven），意思是它可经常处理较大的差分输入电压。相反，对于运算放大器而言，它通常被设计成在较小的信号和差分电压下运行，而这里的反馈概念通常都含有 “过驱” 意义，这样会导致开环配置中的输入出现饱和效应。如果将输入的极性倒转，则过驱时产生的输入级的饱和会导致信号的传播具有一定的延迟或相位滞后。

　　再者，对于较大的差分输入电压来说，运算放大器的输出很容易到达极限输出，从而启动保护功能。保护功能的启动将会导致输入阻抗的量级明显下降，迫使过量的电流涌到输入级，造成过载，甚至过热。如果在设计上没有保护的措施，那便可能导致整个器件损毁。因此，在器件的数据表，通常都会提供器件的最大输入电流的额定值，以帮助设计人员决定用多少附加输入电阻。

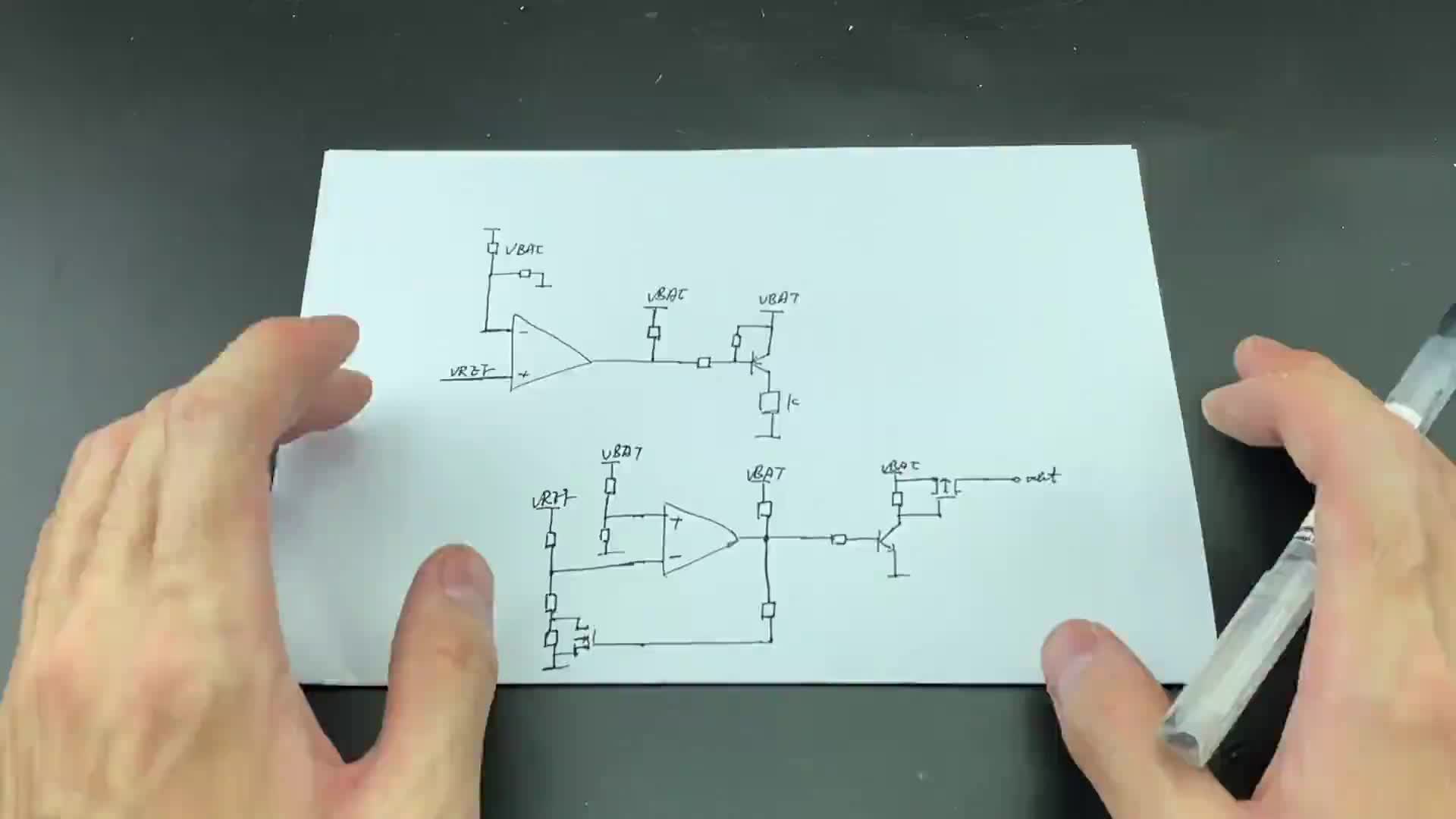
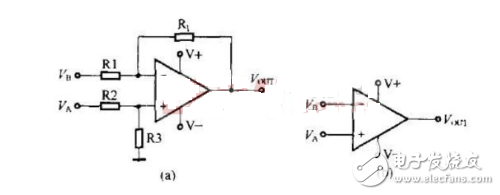
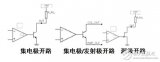
　　比较器和运算放大器之间最基本的区别就是他们具有不同的输出级结构。开漏或开集（以MOSFET为例）输出都有一个可用作输出但却不内部连接到V+的节点，而一个连接正电源电压的外部电阻器会在晶体管被关闭时将输出拉成 “高”。这个外部电压可以高于VCC，并且允许电平移位或可通过平行数个器件的两个或更多个输出来达到所谓的 “Wired-Or”2 功能 。假如内部的晶体管启动，一个细小的电流会从外部电源经过上拉电阻器流进器件输出，并令输出电压级转换成 “低” 和接近VCE （双极晶体管中的集极-发射极电压）。

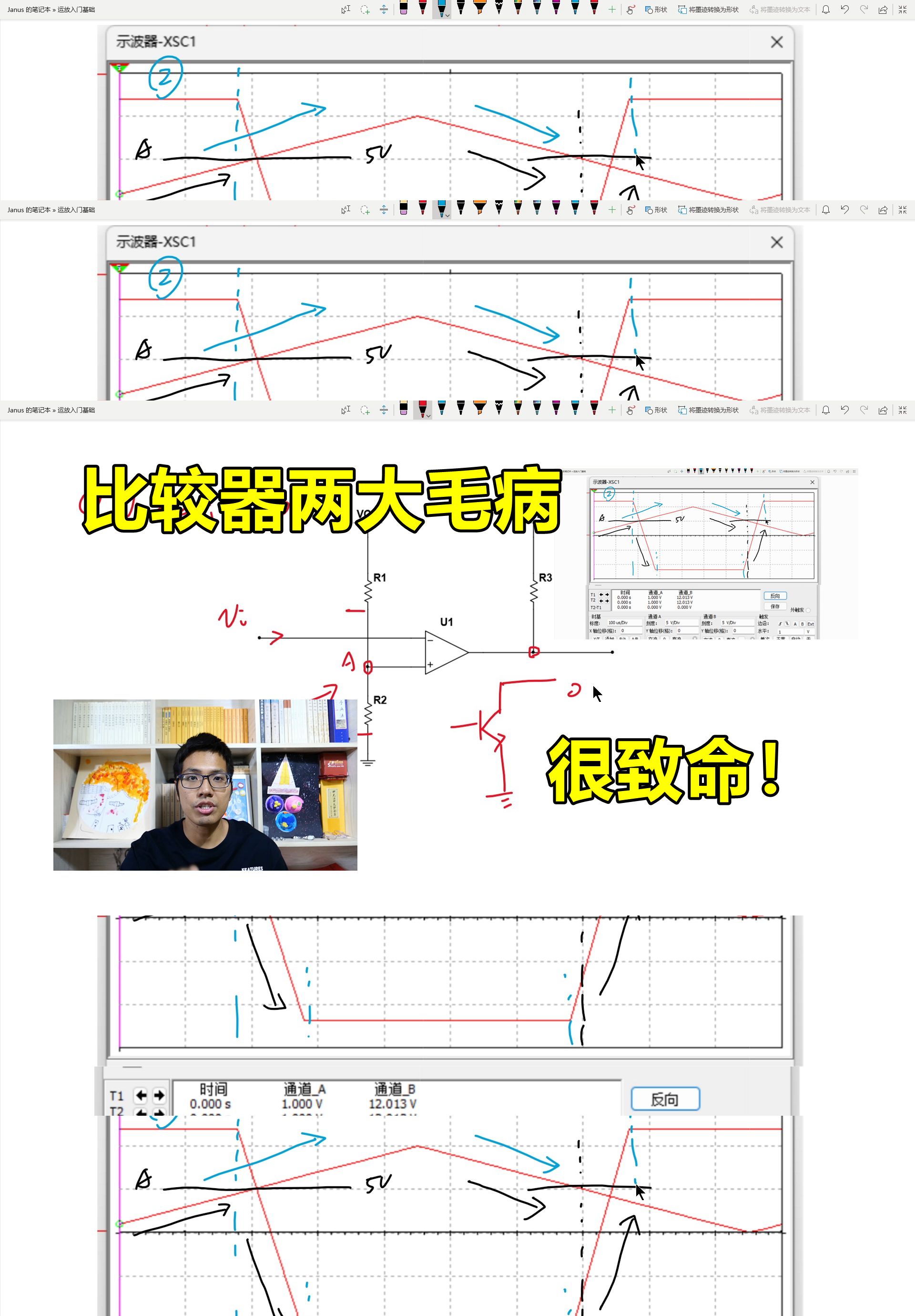
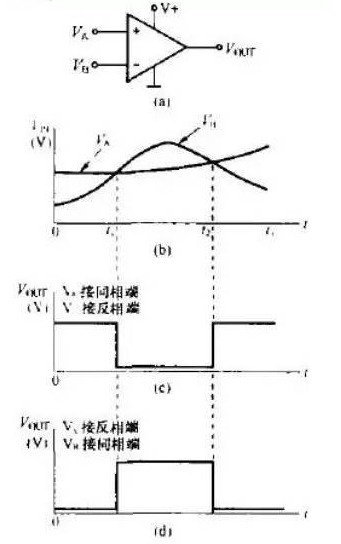
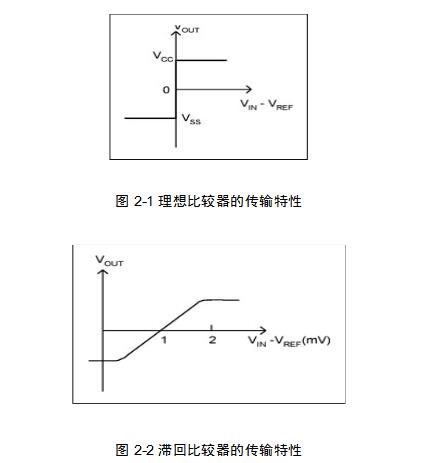
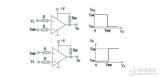
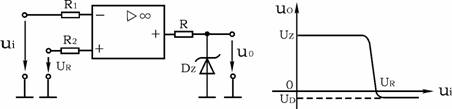
　　比较器通常都不进行频率补偿功能，因此其工作速度相当高，同时开关时间也在某程度上取决于 “过驱”的程度。图1表示出当衡量一个输出状态变化时的差分输入电压。从图中可看出过驱需要高于失调电压才可以保证比较器有效地进行工作。一般来说，较大的过驱可加快开关时间。

　　比较器一般都以参数值和/或功能来分类，例如：

　　

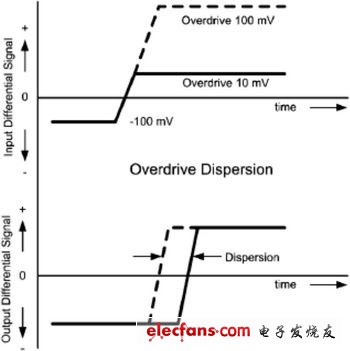
　　图1 输入过驱和相关的传播延迟消散

　　·通用比较器；

　　·高速比较器（传播延迟少于50毫微秒）；

　　·低压比较器（电源电压VCC低于5V）；

　　·微功率比较器（静态电流低于20微安）；

　　·集成参考的比较器。

　　比较器的特性取决于其类别，分别为：

　　·传播延迟—由施加一个差分信号与切换状态的输出级之间的时间延迟 （例如是50%）。

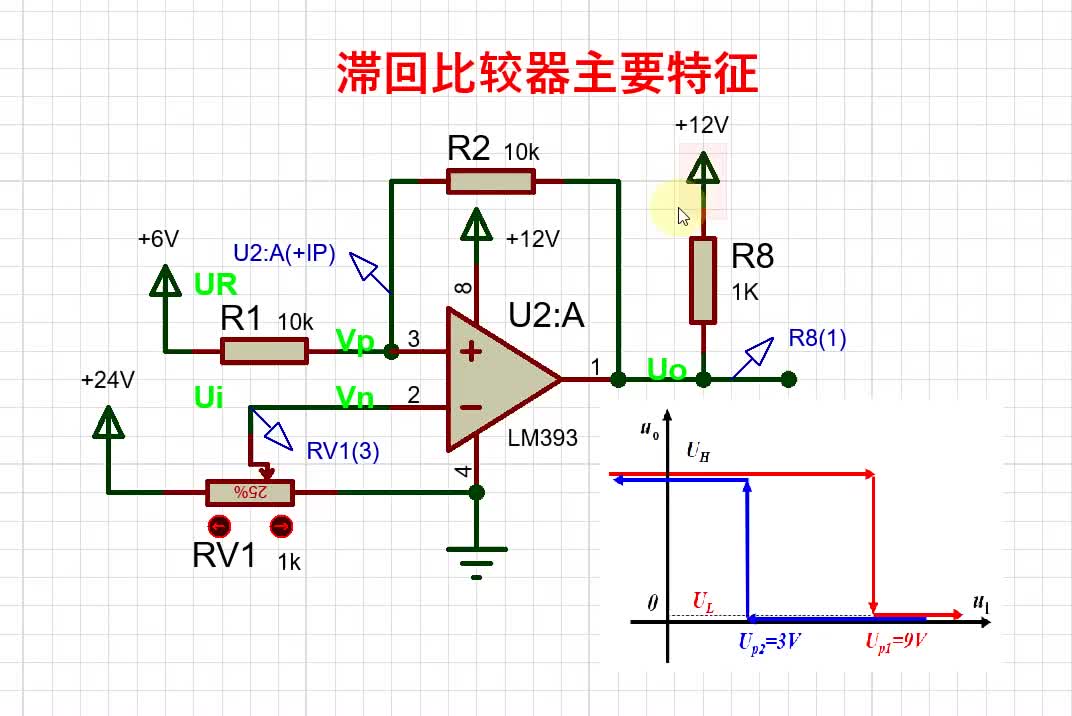
　　·内部或外部滞后— 滞后是一种介乎低到高开关电压和高到低开关电压之间的设计预算中或需激活的差别。有些比较器具备可调节滞后水平的功能，方法是通过在指定的引脚上施加电压。

　　·上升及下降时间—一般是输出电压的10%至90%的时间，并且上升和下降缘的时间可以有差别，假如这情况出现，那将会导致输出的周期时间会相对于输入信号而改变。

　　·触发率—指在某一个频率下，比较器的输出可以跟随输入的状态来变化。

　　·消散—量度传播延迟变化的参数。

　　·抖动—可以是随机或事前决定，负责量度信号缘在时间上的不定性。