电子发烧友App
加法器是产生数的和的装置。加数和被加数为输入，和数与进位为输出的装置为半加器。若加数、被加数与低位的进位数为输入，而和数与进位为输出则为全加器。常用作计算机算术逻辑部件，执行逻辑操作、移位与指令调用。在电子学中，加法器是一种数位电路，其可进行数字的加法计算。在现代的电脑中，加法器存在于算术逻辑单元（ALU）之中。 加法器可以用来表示各种数值，如：BCD、加三码，主要的加法器是以二进制作运算。由于负数可用二的补数来表示，所以加减器也就不那么必要。
加法器电路原理
在计数体制中，通常用的是十进制，它有0，1，2，3，…，9十个数码，用它们来组成一个数。但在数字电路中，为了把电路的两个状态（1态和0态）和数码对应起来，采用二进制较为方便，二进制只有0和1两个数码。
十进制是以10为底数的计数体制，例如
二进制是以2为底数的计数体制，例如
二进制数11011相当于十进制数27。
二进制加法器是数字电路的基本部件之一。二进制加法运算同逻辑加法运算的含义是不同的。前者是数的运算，而后者表示逻辑关系。二进制加法是“逢二进一”，即1+1=10，而逻辑加则为1+1=1。
1、半加器
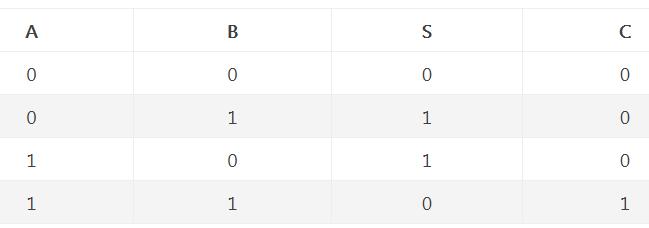
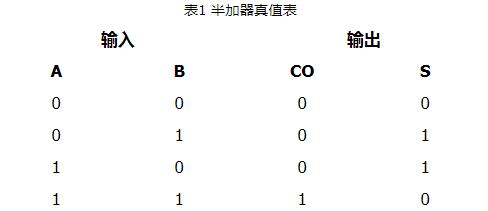
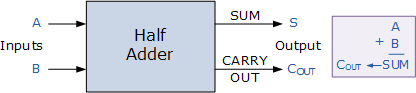
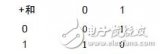
所谓“半加”，就是只求本位的和，暂不管低位送来的进位数。半加器的逻辑状态表见表1。
其中，A和B是相加的两个数，S是半加和数，C是进位数。
由逻辑状态表可写出逻辑式：
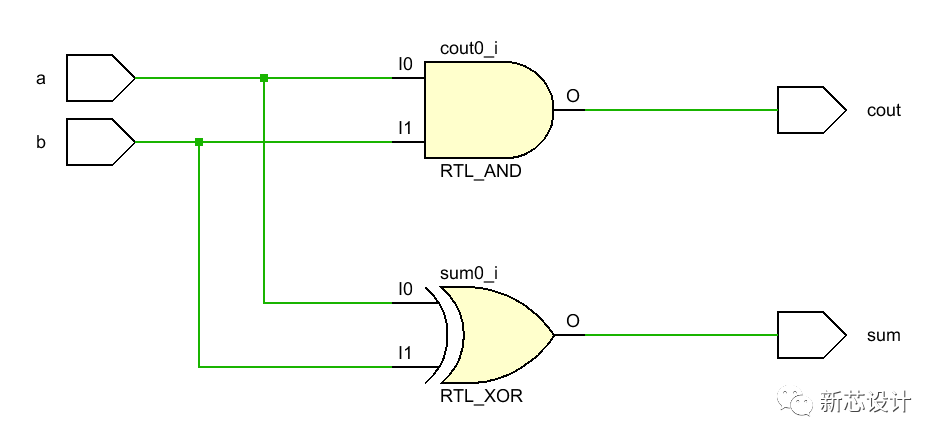
并由此画出图1（a）的逻辑图。图1（b）是半加器的逻辑符号。
图1半加器逻辑图及其逻辑符号
2、全加器
当多位数相加时，半加器可用于最低位求和，并给出进位数。第二位的相加有两个待加数
，还有一个来自低位送来的进位数。这三个数相加，得出本位和数（全加和数）
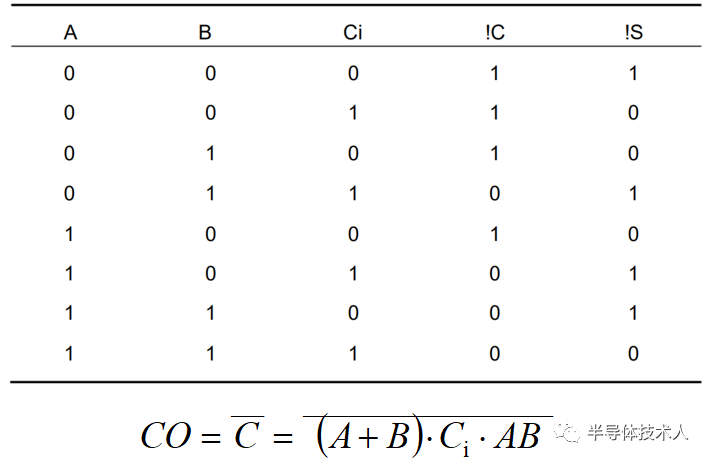
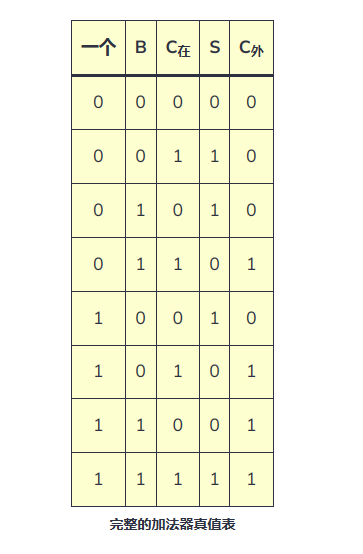
和进位数
，这就是“全加”，表2是全加器的逻辑状态表
全加器可用两个半加器和一个或门组成，如图2（a）所示。
在第一个半加器中相加，得出的结果再和
在第二个半加器中相加，即得出全加和
。两个半加器的进位数通过或门输出作为本位的进位数
。图2（b）是全加器的逻辑符号。
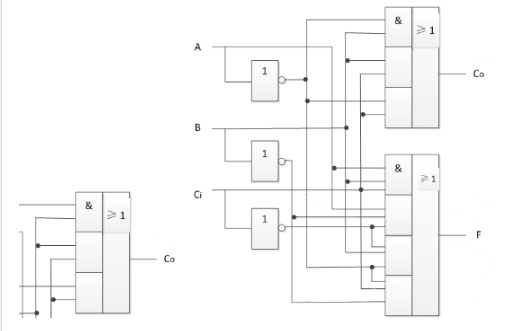
图2 全加器逻辑图及其逻辑符号
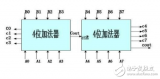
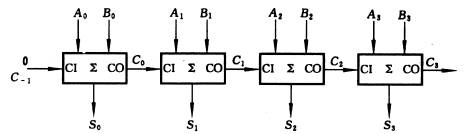
例1、用4个全加器组成一个逻辑电路以实现两个4位的二进制数A—1101（十进制为13）和B—1011（十进制为11）的加法运算。
解：
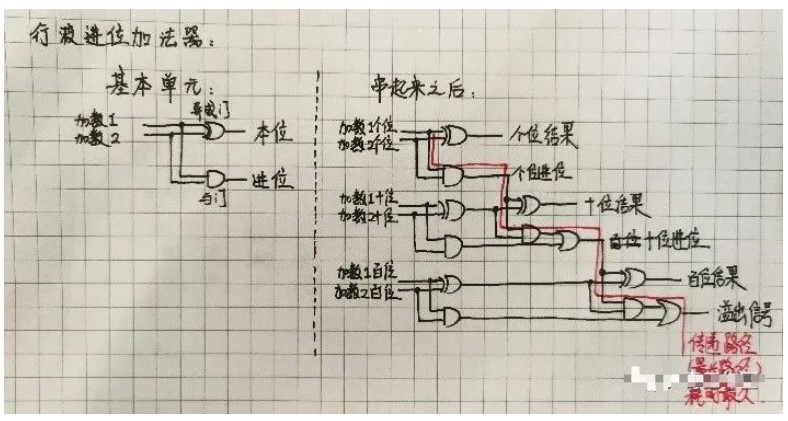
逻辑电路如图3所示，和数是S—11000（十进制数为24）。根据全加器的逻辑状态表自行分析。
这种全加器的任意一位的加法运算，都必须等到低位加法完成送来进位时才能进行。这种进位方式称为串行进位，它的缺点是运算速度慢，但其电路比较简单，因此在对运算速度要求不高的设备中，仍不失为一种可取的全加器。T692集成加法器就是这种串行加法器。
图3 例1的逻辑图
二进制加法器原理
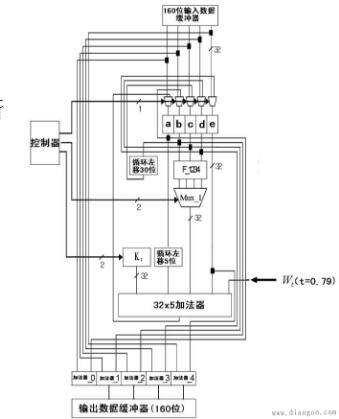
被加数和加数的各位能同时并行到达各位的输入端，而各位全加器的进位输入则是按照由低位向高位逐级串行传递的，各进位形成一个进位链。由于每一位相加的和都与本位进位输入有关，所以，最高位必须等到各低位全部相加完成并送来进位信号之后才能产生运算结果。显然，这种加法器运算速度较慢，而且位数越多，速度就越低。？ 为了提高加法器的运算速度，必须设法减小或去除由于进位信号逐级传送所花的时间，使各位的进位直接由加数和被加数来决定，而不需依赖低位进位。根据这一思想设计的加法器称为超前进位（又称先行进位）二进制并行加法器。对于1位的二进制加法，相关的有五个的量：1、被加数A，2、被加数B，3、前一位的进位CIN，4、此位二数相加的和S，5、此位二数相加产生的进位COUT。前三个量为输入量，后两个量为输出量，五个量均为1位。对于32位的二进制加法，相关的也有五个量：1、被加数A（32位），2、被加数B（32位），3、前一位的进位CIN（1位），4、此位二数相加的和S（32位），5、此位二数相加产生的进位COUT（1位）。要实现32位的二进制加法，一种自然的想法就是将1位的二进制加法重复32次（即逐位进位加法器）。这样做无疑是可行且易行的，但由于每一位的CIN都是由前一位的COUT提供的，所以第2位必须在第1位计算出结果后，才能开始计算；第3位必须在第2位计算出结果后，才能开始计算，等等。而最后的第32位必须在前31位全部计算出结果后，才能开始计算。
利用74LS138和与非门设计两个二进制全加器
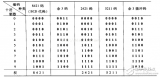
设A为加数B为被加数 低位进位为Ci-1 和为S 进位为Ci
A B Ci-1 S Ci
0 0 0 0 0
0 0 1 1 0
0 1 0 1 0
0 1 1 1 1
1 0 0 1 0
1 0 1 0 1
1 1 0 0 1
1 1 1 1 1
___________
— — — —
S=Y1.Y2.Y4.Y7
___________
— — — —
Ci=Y3.Y5.Y6.Y7
工商网监
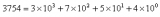
评论