PID控制是业内最常见的控制算法,在工业控制领域有很高的接受度。 PID控制器的广泛应用,得益于其在多种操作条件下稳定的性能,以及易操作的特性。工程师可以用简单直观的方式实现PID控制。
PID控制有三个基本要件:比例(proportional)、积分(integral)、微分(derivative)。通过这三种不同的计算方法获取最优化的结果。 本文主要介绍闭环系统、PID经典理论、闭环控制系统整定等主题。 LabVIEW中的PID工具包和PID VI也在本文的讨论范围之内。
1. 控制系统
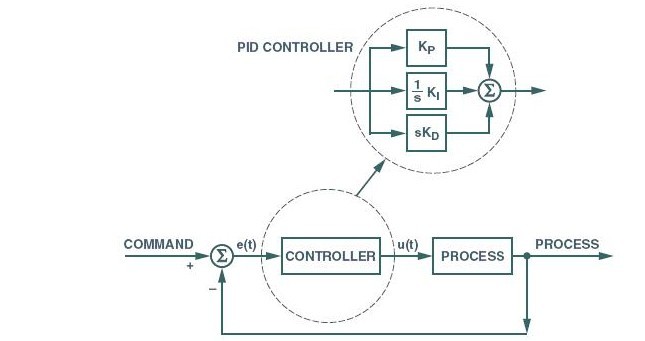
PID控制器的基本理念是读取感应器,根据计算比例、积分、微分响应得出期望的激励器输出,将三个值相加计算输出。 开始定义PID控制器之前,要先了解闭环系统及其相关术语。
闭环系统
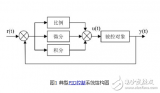
在一个典型的控制系统里,过程变量是需要被控制的系统变量。例如,温度(ºC)、压强(psi)、流速(升/分钟)。 传感器用来测量过程变量,并对控制系统做出反馈。 设定值是过程变量的期望值或必须达到的值。例如,在一个温控系统中,设定温度值为100摄氏度。 在任意时间点上,控制系统算法(补偿器)使用过程变量和设定值之间的差值,得到期望的激励器输出,驱动系统(设备)。 例如,如测量得到的温度过程变量为100 ºC,期望的温度设定值为120 ºC,控制器算法的激励器输出将指示打开加热器。 打开加热器,整个系统就逐渐变热,温度过程变量测得的结果也会增加。 这就是一个闭环控制系统,读取传感器,提供即时反馈,计算期望的激励器输出,这三项操作以固定速率循环往复,如图1所示。
在很多情况下,激励器输出不是对系统有影响的唯一信号。 例如,在温度舱内,可能会有冷空气源。冷空气吹入舱内时,会扰动环境温度。这类扰动因素叫做干扰。 设计控制系统时,通常会尽可能减少对过程变量的干扰因素。
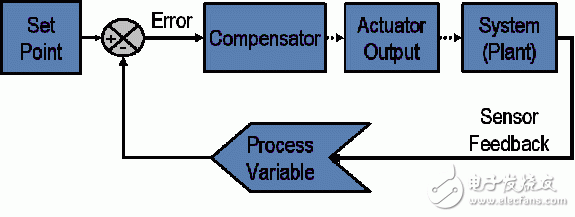
图1:典型闭环系统的示意图
术语定义
控制设计过程从定义性能需求开始。 控制系统的性能一般通过应用一个阶跃函数作为设定值命令变量,然后测量过程变量的响应。 一般来说,通过测量定义的波形特征来量化响应。 上升时间是系统从稳定状态(或最终值)的10%上升到90%所需的时间。 过冲百分比是过程变量超过最终值的百分比数,以最终值的百分比表示。 稳定时间是过程变量值稳定在最终值5%范围内所需的时间。 稳定状态误差是过程变量和设定值之间的差值。 这些值的确切定义在学术和工业上的定义不尽相同。
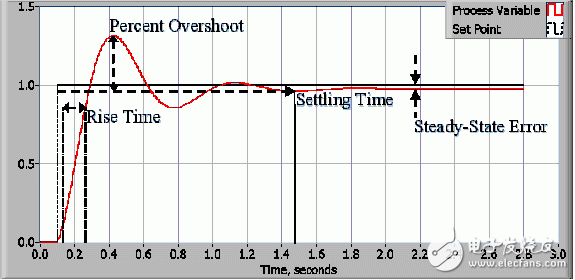
图2:典型闭环系统的响应
使用这些量来定义控制系统的性能要求时,需定义控制系统满足这些需求时可能遇到的“最坏情况”。 一般而言,系统中都有一个影响过程变量或过程变量测量值的干扰。 所以,要设计一个在最坏情况下都能满意工作的控制系统。 控制系统克服干扰的能力,被称为控制系统的干扰抑制。
在某些情况下,对于一个给定控制输出的系统反馈可能会因时间变化。 在非线性系统中,控制参数在某个时刻给出的期望响应,但是在另一个时刻可能无法给出满意的响应。 例如,舱室中几乎为空时,其对加热器输出的响应比舱室填满或几乎填满液体时更快。 控制系统对干扰和非线性的耐受度,被称为控制系统的稳定性。
有些系统会出现非预期的不响应期。 不响应期是过程变量改变和观测到该改变之间的时间延迟。 例如,如温度传感器离冷水阀较远,传感器无法立即监测到冷水阀打开或关闭。 不响应期也可能是因为系统或输出激励器响应控制命令比较缓慢。例如,阀门打开和关闭的速度很缓慢。 在化工厂,造成不响应期的常见原因是化学试剂在管道中流通需要时间。
循环周期也是闭环系统的重要参数。 调用控制算法之间的时间间隔是循环周期时间。 变化迅速或操作复杂的系统,需要更快的循环速率。
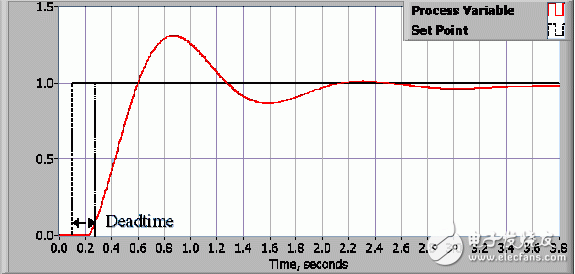
图3:闭环系统的响应及其不响应期
一旦指定了性能需求,即可开始检查系统并选择合适的控制方案。 在大多数应用中,PID控制程序必须提供结果。
2. PID理论
比例响应
比例模块取决于设定值和过程变量之间的差值。 这个差值被称为“误差”。 比例增益 (Kc)决定了输出响应对误差信号的比例。 例如,误差为10,比例增益为5时,比例响应为50。一般而言,提高比例增益会增加控制系统响应的速度。 但是,如果比例增益太大,过程变量会有振荡。 如果继续增加Kc,系统振荡会越来越大,以至于超出控制,使得系统变得不稳定。
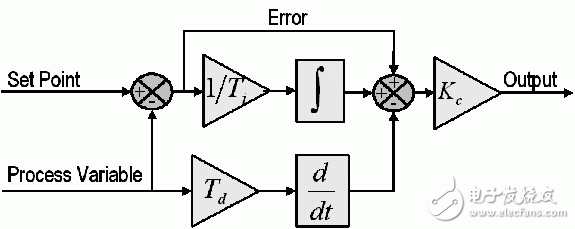
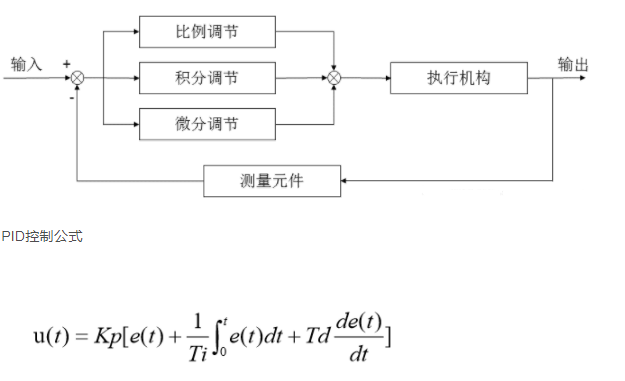
图4:基本PID控制算法的示意图
积分响应
积分模块将一段时间内的误差相加。 即使是一个很小的误差,也会让积分响应缓慢增加。 积分响应会根据时间持续增加,除非误差为0。积分响应的目的在于将稳定状态的误差保持在0。 稳定状态误差是过程变量和设定值之间的差值。 当积分操作满足了控制器的条件,而控制器还未将误差保持在0时,会产生积分饱和的结果。
微分响应
微分模块在过程变量迅速增大时停止输出。 微分响应与过程变量变化的速度之间成比例关系。 增加微分时间(Td)会使控制系统对误差的反应更加剧烈,会增加整个控制系统的响应时间。 大多数实用控制系统使用非常小的微分时间(Td),因为微分响应对过程变量的噪声特别敏感。 如传感器反馈信号中有噪声或控制循环速率太低,微分响应会使控制系统变得不稳定。
3. 整定
设置P、I、D最佳增益,从而得到控制系统理想反馈的过程叫做整定。 整定方法有很多种。本文主要介绍试错法和Ziegler Nichols法。
可通过试错法获得PID控制器的增益。 当了解了每个增益参数的有效性后,该方法就变得相对简单。 在该方法中,先将I、D设置为0,比例增益增加到循环输出开始振荡为止。 增加比例增益时,系统变得更快,但是要保证系统不会变得不稳定。 一旦设置P去获取期望的快速响应,积分项会增加以停止振荡。 积分项会减少稳定状态的误差,但是会增加过冲。 合理的过冲对于一个快速系统来说是必要的,这样才能立即响应变化。 调整积分项,可达到最小稳定状态误差。 一旦设置了P、I获取有最小稳定状态误差的快速控制系统,微分项会一直增加直到循环对于设定值来说足够快。 增加微分项会减少过冲,产生更高的稳定性增益,但系统会对噪声变得异常敏感。 大多数情况下,工程师在设计时,需要权衡控制系统的各种特性,然后进行取舍。
Ziegler-Nichols是整定PID控制器的通用方法。 该方法与试错方法类似,将I、D设置为0,P增加到循环开始振荡为止。 一旦发生振荡,需观察关键增益Kc和振荡周期Pc。 然后根据下表所示调整P、I、D。

表1:Ziegler-Nichols整定,使用振荡法
4. NI LabVIEW和PID
LabVIEW PID工具包为PID控制系统设计提供各种简单易用的VI。 PID VI具有控制输出范围限制、集成器防饱和、对PID增益改动稳定输出等功能。 PID高级VI包括PID VI的所有功能。此外,PID VI还有非线性积分、双自由度控制和误差平方控制等功能。

图5:LabVIEW PID控制选板上的VI
PID选板上还有一些高级VI。例如,PID自整定VI、PID增益调度VI,等等。 PID自正定VI用于优化控制系统的PID参数。 给出P、I、D的估计值后,PID自整定VI帮助优化PID参数,从而获取控制系统的最佳响应。

图6:LabVIEW PID控制选板上的高级VI
使用实时终端上的LabVIEW Real-Time模块后,控制系统的可靠性大幅提高。 National Instruments提供M系列数据采集卡,与一般的控制系统相比,具有更高的精度和性能。
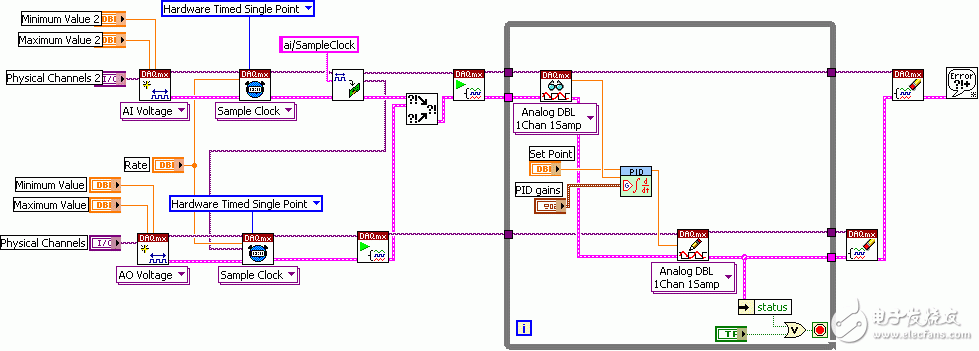
图7:使用NI采集设备的PID控制VI
LabVIEW与M系列板卡的紧密集成极大地减少了开发时间,提高了工程师的效率。 图7显示了使用M系列数据采集设备和NI-DAQmx API的PID VI。
5. 总结
PID控制算法是可靠且简便的控制算法,在业内使用广泛。 该算法灵活度高,在各种应用中表现优异,被广泛认可。 NI LabVIEW和NI数据采集设备具有更高的精度和性能,帮助您搭建一个出色的PID控制系统。
6. 参考资料
1. Classical PID Control
by Graham C. Goodwin, Stefan F. Graebe, Mario E. Salgado
Control System Design, Prentice Hall PTR
2. PID Control of Continuous Processes
by John W. Webb Ronald A. Reis
Programmable Logic Controllers, Fourth Edition, Prentice Hall PTR
 电子发烧友App
电子发烧友App












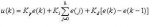












评论