为什么锁相放大器抗噪能力强 - 锁相放大器降噪，为什么锁相放大器抗噪能力强？

　　为什么锁相放大器抗噪能力强

　　锁相放大器不容易受到噪声影响的原因，是因为很好地利用了噪声（白噪声）与目的信号（正弦波）之间在性质上的差别。在这里，我们一方面整理白噪声的性质和正弦波的性质，一方面解说为什么锁相放大器会具有很强的噪声抑制能力。

　　1、平坦的频谱

　　在宽阔的频率范围内，该信号具有几乎相同的频谱。信号的瞬时电平成为预测不到的随机的值。

　　2、随着频带宽度不同测量电压会改变

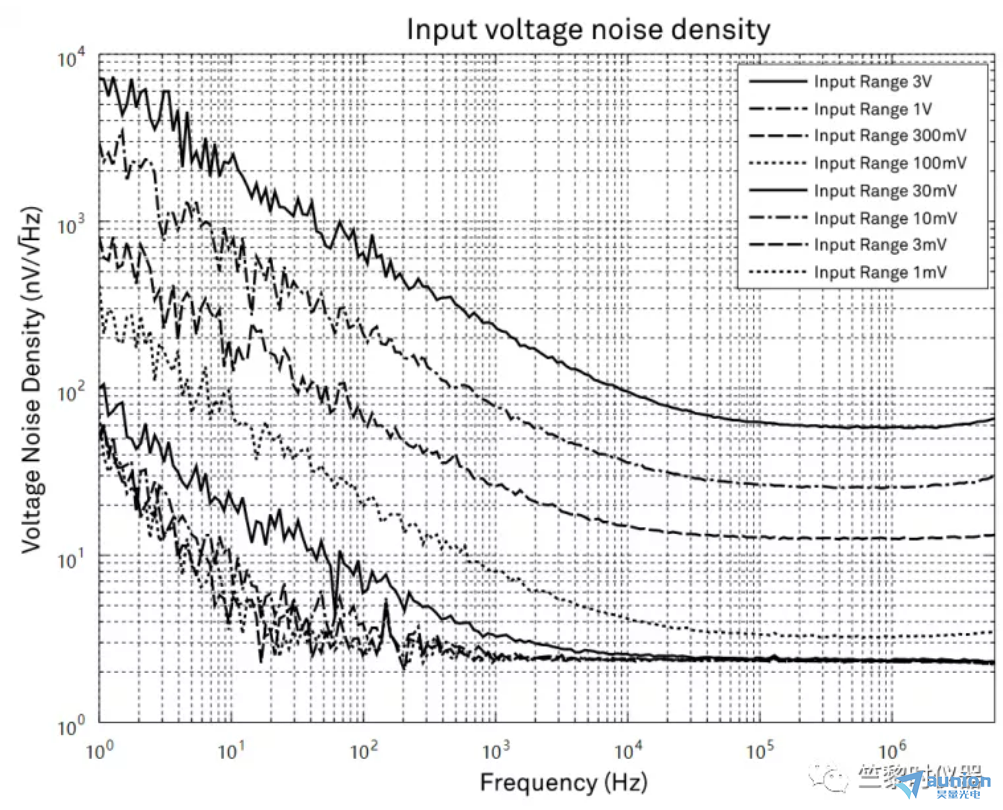
　　在用毫伏计测量白噪声时，得到的测量值和白噪声所具有的频谱带宽（BandWidth： B.W.）的平方根以及电平成比例。测量得到的电压值，与下图中的浅蓝色部分的面积成比例。

　　即使对于同样的噪声，如果用带通滤波器（BPF）来限制所通过的频带，那么测量所得的电压值就会不同。

　　把测量所得的噪声电压（Vrms），除以频带宽度的平方根，就得到用表示噪声大小的单位、也即称作噪声电压密度（V/√Hz）来衡量的值。频道宽度如果缩小到1/100，那么测量所得的噪声电压就缩小到1/10。

　　3、频谱非常集中

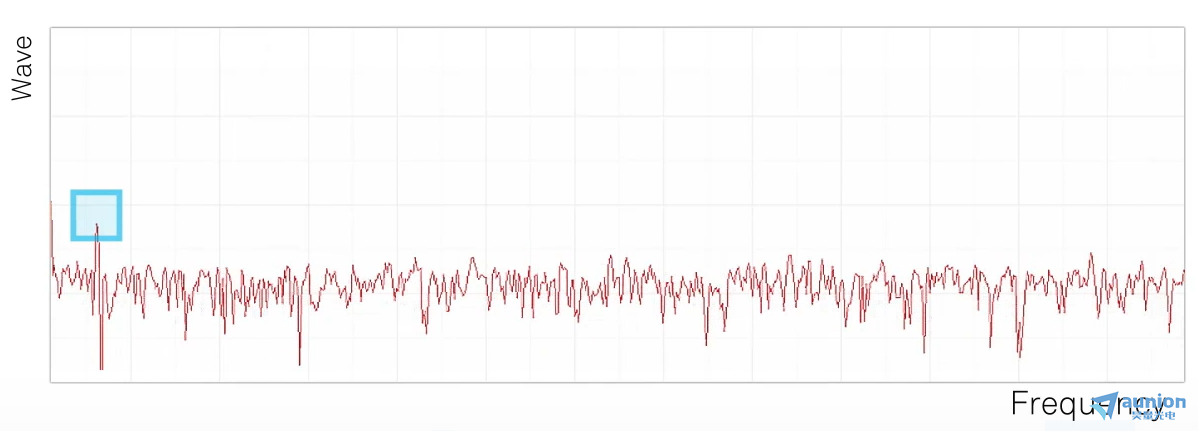
　　1kHz正弦波信号的频谱，只存在于1kHz的位置，其他地方的频谱的电平都为零。

　　4、与频带宽度无关，测量所得电压保持一定的值

　　因为频谱是集中分布的，所以不受频带宽度的影响，测量所得的电压保持一定的值。但是，必须要使信号频率存在于所取的频带之内。用交流电压表所测量的电压值，与频带宽度无关，是上图中的V。那么，在正弦波上叠加了白噪声以后会怎么样呢？

　　即使白噪声与正弦波进行加法运算所得的信号，测量所得的电压对于频带宽度所具有的各种性质也不会有变化。所以，当带通滤波器的频带宽度变狭窄时，就会有以下结果：

　　想要测量的信号的电平不变；白噪声的强度减小；交流声等频率不同的成分也当然被削弱。

　　从以上这些结果可知，为了测量被噪声所掩埋的信号，应该将带通滤波器的频带宽度变窄。如果将频带宽度缩小到1/N，那么噪声就减小到1/√N，而信号却不改变，其结果SN比（信噪比）改善为1/√N。

　　但是，这样的带通滤波器也是有一个限度的。为了说明「锁相放大器利用了噪声与目的信号所具有的不同性质，所以不容易受到噪声的影响」，前面已解说了以下几个要点：

　　噪声（白噪声）的性质；正弦波的性质；从白噪声与正弦波合成的信号中，使用带通滤波器可以使目的信号（正弦波）从噪声中浮现出来。

　　5、使通带变狭窄的限度

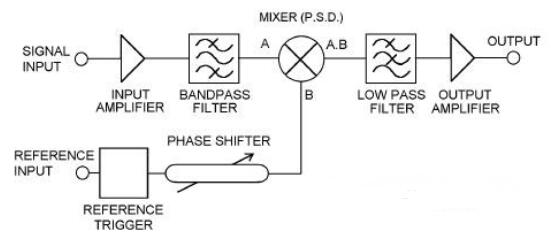
　　使用带通滤波器只让想要测量的频率信号通过，可以抑制噪声，让目的信号浮现出来。但是，使带通滤波器的通带宽度变窄，这也是有限度的。

　　在带通滤波器中，中心频率与通带宽度的比值称作Q值，作为衡量带通滤波器的滤波尖锐程度的一项指标来使用。

　　Q值越大，通带宽度就越窄，抑制噪声的能力就越强。但是，一般的滤波器所能够实现的Q值，大约在100左右。对于1kHz的中心频率，相应的通带宽度的限界大约在10Hz左右。Q值不能任意增大的原因，在于组成滤波器的零部件的精确度和时间/温度的稳定性是有限的。