同向放大器 - 如何用”虚短“和”虚断“分析运放电路

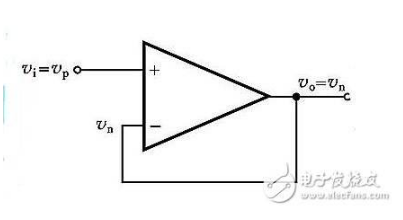
　　2）同向放大器：

　　

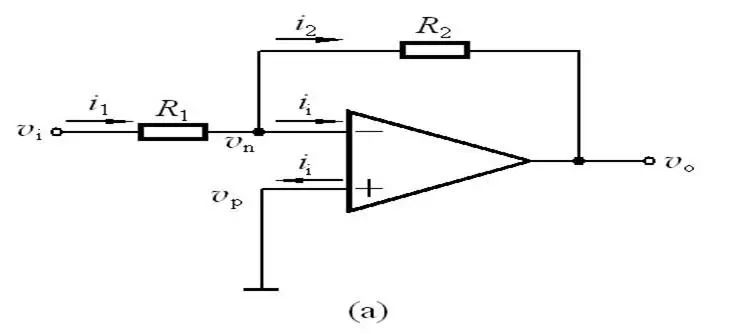
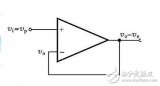
　　图2

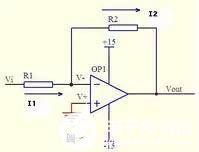
　　图二中Vi与V-虚短，则 Vi = V- ……a

　　因为虚断，反向输入端没有电流输入输出，通过R1和R2 的电流相等，设此电流为I，由欧姆定律得： I = Vout/（R1+R2） ……b

　　Vi等于R2上的分压， 即：Vi = I*R2 ……c

　　由abc式得Vout=Vi*（R1+R2）/R2 这就是传说中的同向放大器的公式了。

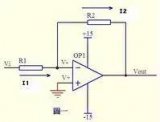
　　3）加法器1：

　　

　　图3

　　图三中，由虚短知： V- = V+ = 0 ……a

　　由虚断及基尔霍夫定律知，通过R2与R1的电流之和等于通过R3的电流，故 （V1 – V-）/R1 + （V2 – V-）/R2 = （V-–Vout）/R3 ……b

　　代入a式，b式变为V1/R1+ V2/R2 = Vout/R3 如果取R1=R2=R3，则上式变为-Vout=V1+V2，这就是传说中的加法器了。

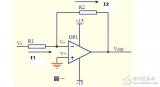
　　4）加法器2：

　　

　　图4

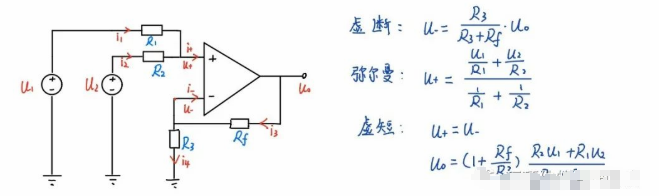
　　请看图四。因为虚断，运放同向端没有电流流过，则流过R1和R2的电流相等，同理流过R4和R3的电流也相等。

　　故 （V1 – V+）/R1 = （V+ - V2）/R2 ……a

　　（Vout – V-）/R3 =V-/R4 ……b

　　由虚短知： V+ = V- ……c 如果R1=R2，R3=R4，则由以上式子可以推导出 V+ = （V1 + V2）/2 V- = Vout/2 故 Vout = V1 +V2 也是一个加法器，呵呵！

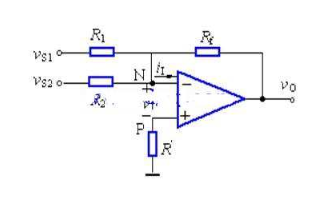
　　5）减法器

　　

　　图5

　　图五由虚断知，通过R1的电流等于通过R2的电流，同理通过R4的电流等于R3的电流，故有 （V2– V+）/R1 = V+/R2 ……a

　　（V1 – V-）/R4 = （V- - Vout）/R3 ……b

　　如果R1=R2， 则V+ = V2/2 ……c

　　如果R3=R4， 则V- = （Vout + V1）/2 ……d

　　由虚短知 V+ = V- ……e

　　所以 Vout=V2-V1 这就是传说中的减法器了。

　　6）积分电路：

　　

　　图6

　　图六电路中，由虚短知，反向输入端的电压与同向端相等，

　　由虚断知，通过R1的电流与通过C1的电流相等。

　　通过R1的电流 i=V1/R1

　　通过C1的电流i=C*dUc/dt=-C*dVout/dt

　　所以 Vout=（（-1/（R1*C1））∫V1dt 输出电压与输入电压对时间的积分成正比，这就是传说中的积分电路了。

　　若V1为恒定电压U，则上式变换为Vout = -U*t/（R1*C1） t 是时间，则Vout输出电压是一条从0至负电源电压按时间变化的直线。