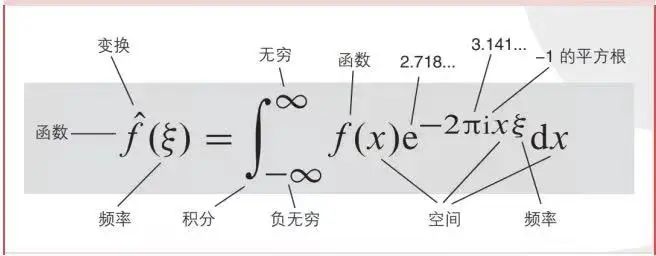
傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。
傅里叶变换怎么发现的
傅里叶分析方法的建立有过一段漫长的历史,涉及到很多人的工作和许多不同物理现象的研究。利用“三角函数和”的概念(也即,成谐波关系的正弦和余弦函数或周期复指数函数的和)来描述周期性过程至少可以追溯到古代巴比伦人时代,当时他们利用这一想法来预测天体运动。这一问题目的近代历史始于1748年欧拉在振动弦的研究工作中。图3.1画出了弦振动的前几个标准振荡模式。如果用f(t,x)来表示弦在时间z和沿着弦的某 横向距离x处的垂直偏离,则对任意固定时刻t来说,所有这些振荡模式均为x的正弦函数,并成谐波关系。
欧拉得出的结论是:如果在某一时刻振动弦的形状是这些标准振荡模的线性组合,那么在其后任何时刻,振动弦的形状也都是这些振荡模的线性组合。另外,欧拉还证明了在该线性组合中,其后面时间的加权系数可以直接从前面时间的加权系数中导得。与此同时,欧拉还完成了相同的计算形式,这一点将在下一节导出有关三角函数和的一个性质中看到, 这些性质使三角函数和的概念在LTI系统分析中变得十分有用。具体地说就是:如果一个LTI系统的输入可以表示为周期复指数或正弦信号的线性组合,则输出也一定能表示成这种形式;并且输出线性组合中的加权系数是直接与输入中对应的系数有关的。
显然,除非很多有用信号都能用复指数的线性组合来表示,否则上面所讨论的性质就不会是特别有用的。在18世纪中期,这一点曾是激烈争论的主题。1753年D·伯努利(D. Bernoulli)曾经声称:一根弦的实际运动都可以用标准振荡模的线性组合来表示。但是,他并投有继续从数学上深入探求下去;问时,在当时他的想法也并未被广泛接受。
事实上,欧拉本人后来也抛弃了三角级数的想法,并且在1759年J.L.拉格朗日(J.L.Lagrange)也曾强烈批评使用三角级数来研究振动弦运动的主张。他反对的论据是基于他自己的信念,即不可能用三角级数来表示一个具有间断点的函数。因为振动弦的波形是由拨动弦而引起(即把弦绷紧再松开),所以拉格朗日认为三角级数的应用范围非常有限。

正是在这种多少有些敌意和怀疑的处境下,J.B.J.傅里叶(Jean Baptiste Joseph Fourier)约于半个世纪后提出了他自己的想法。傅里叶1768年3月21日生于法国奥克斯雷(Allxerre), 到他加入这场有关三角级数论战的时候,他已有了相当的阅历。他当时进行研究所处的境遇使他的很多贡献(特别是以他的名字命名的级数和变换)更是令人难忘。
他的重大发现虽然在他自己的有生之年没有得到完全的承认,但是,却已对数学这门学科的发展产生了深刻的影响,并在极为广泛的科学和工程领域内一直具有并仍然继续具有很大的价值。
除了他在数学方面的研究外,傅里叶还有一段活跃的政治生涯。事实上,就在法国大革命后的那些年代里,他的一些活动几乎导致他的垮台。因为曾经有两次,他都差一点走上了断头台。其后,傅里叶又成为N.波拿马(Napsleon Bonaparle)的伙伴而跟随着他远征埃及(在此期间,傅里叶搜集了后来作为他的“埃及学”论文基础的有关资料)。在1802年被波拿马任命为法国某一地区的行政长官,就在他任职行政长官的期间,傅里叶构思了关于三角级数的想法。
热的传播和扩散现象是导致傅里叶研究成果的实际物理背景。在当时数学物理学领城中大多数前人的研究巳经涉及到理论力学和天体力学的背景下,这一问题本身就是十分有意义的一步。到了1807年,傅里叶已经完成了一项研究,他发现在表示一个物体的温度分布时,成谐波关系的正弦函数级数是非常有用的。
另外,他还断言:“任何”周期信号都可以用这样的级数来表示!?虽然在这一问题上他的论述是很有意义的,但是,隐藏在这一问题后面的其它很多基本概意己经被其他科学家们所发现;同时,傅里叶的数学证明也不是很完善的。后来于1829年,P.L.狄里赫利(P.L.Dirichlet)给出了若干精确的条件,在这些条件下,一个周期信号才可以用一个傅里叶级数表示。因此,傅里叶实际上并没有对傅里叶级数的数学理论做出什么贡献。然而,他确实洞察出这个级数表示法的潜在威力,井且在很大程度上正是由于他的工作和断言,才大大激励和推动了傅里叶级数问题的深入研究。
另外,傅里叶在这一问题上的研究成果比他的任何先驱者都大大前进了一步,这指的是他还得出了关于非周期信号的表示——不是成谐被关系的正弦信号的加权和,而是不全成谐波关系的正弦信号的加权积分。这就是第4和第5章所关注的从傅里叶级数到傅里叶积分(或变换)的推广。和傅里叶级数一样,傅里叶变换仍然是分析LTI系统最强有力的工具之一。
当时指定了4位著名的数学家和科学家来评审1807年傅里叶的论文,其中3位即S.F.拉克劳克斯(S.F.Lacroix)、G.孟济(G.Monge)和P.S.拉普拉斯(P.S.Laplace)赞成发表傅里叶的论文,而第四位J.L.拉格朗日仍然顽固地坚持他于50年前就已经提出过的关于拒绝接受三角级数的论点。
由于拉格朗日的强烈反对,傅里叶的论文从未公开露面过。为了使他的研究成果能让法兰西研究院接受并发表,在经过了几次其它的尝试以后,傅里叶才把他的成果以另一种方式出现在“热的分析理论”这本书中。这本书出版于1822年,也即比他首次在法兰西研究院宣读他的研究成果时晚15年!
直到傅里叶的晚年,他才得到了某种应有的承认!但是,对他来说最有意义的称赞是他的研究成果已经在数学、科学和工程等如此众多的领域内产生的巨大影响。傅里叶级数和积分的分析在很多数学问题中都留下了它的足迹,积分理论、点集拓扑和特征函数展开等仅是这方面的几个例子。再者,除了最初在振动问题和传热问题的研究外,在科学和工程领域中有大量的其它问题,正弦信号(从而傅里叶级数和变换)在其中起着很重要的作用。
例如,在描述行星运动和反映地球气候的周期性变化中,很自然地会出现正弦信号;交流电源产生的正弦电压和电流;以及我们将要看到的,傅里叶分析方法能够用来分析LTI系统的响应,比如一个电路对正弦输入的响应等。同时,海浪也是由不同波长的正弦波的线性组合所组成的;无线电台和电视台发射的信号都是正弦的;以及依据傅里叶分析可以给出任何文本的快边阅读等等。总之,正弦信号和傅里叶分析方法的应用范围远远超出以上所列举的这几个例子。
在前面一段中的许多应用,以及傅里叶和他的问伴们在数学物理学方面的最初研究都是集中在连续时间内的现象。与此同时,对于离散时间信号与系统的傅里叶分析方法却有着它们自己不同的历史根基,并且也有众多的应用领域。尤其是,离散时间概念和方法是数值分析这门学科的基础。
用于处理离散点集以产生数值近似的有关内插、积分和微分等方面的公式远在17世纪的牛顿时代就被研究过。另外,在已知一组天体观察数据序列下,预测某一天体运动的问题在18和19世纪曾吸引着包括高斯(Gauss)在内的许多著名科学家和数学家从事调和时间序列的研究,从而为大量的初始工作能在离散时间信号与系统下完成提供了第二个舞台。
在20世纪60年代中期,一种称之为快速傅里叶变换(FFT)的算法被引入。这一算法在1965年被库利(Cooley)和图基(Tukey)独立地发现,其实它也有相当长的历史。事实上,这一算法在高斯的手稿中已能找到。
之所以使得它成为重要的近代发现是由于FFT证明是非常适合于高效的数字实现,并且它将计算变换所需要的时间减少了几个数量级。有了这一算法,在利用离散时间傅里叶级数和变换中许多有兴趣而过去认为不切实际的想法突然变得实际起来,井且使离散时间信号与系统分析技术的发展加速向前迈进。
由这样一个很长历史的发展所涌现出的,对于连续时间和离散时间信号与系统分析来说是一个强有力而严谨的分析体系,以及有着极为广泛的现存和潜在的应用范倒。这一章和后续几章将建立这个体系中的一些基本方法,井研究其中某些重要的内涵。
傅里叶变换有什么用
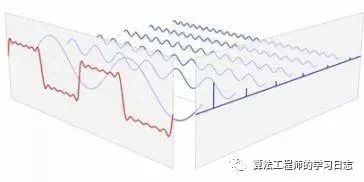
尽管最初傅里叶分析是作为热过程的解析分析的工具,但是其思想方法仍然具有典型的还原论和分析主义的特征。“任意”的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式,而正弦函数在物理上是被充分研究而相对简单的函数类,这一想法跟化学上的原子论想法何其相似!奇妙的是,现代数学发现傅里叶变换具有非常好的性质,使得它如此的好用和有用,让人不得不感叹造物的神奇:

傅里叶变换是线性算子,若赋予适当的范数,它还是酉算子;
傅里叶变换的逆变换容易求出,而且形式与正变换非常类似;
正弦基函数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解。在线性时不变的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取;
著名的卷积定理指出:傅里叶变换可以化复杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段;
离散形式的傅里叶变换可以利用数字计算机快速的算出(其算法称为快速傅里叶变换算法(FFT))。
正是由于上述的良好性质,傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。
有关傅里叶变换的FPGA实现
傅里叶变换是数字信号处理中的基本操作,广泛应用于表述及分析离散时域信号领域。但由于其运算量与变换点数N的平方成正比关系,因此,在N较大时,直接应用DFT算法进行谱变换是不切合实际的。然而,快速傅里叶变换技术的出现使情况发生了根本性的变化。本文主要描述了采用FPGA来实现2k/4k/8k点FFT的设计方法。
 电子发烧友App
电子发烧友App























评论