有了“1”,还要有“0”才能构成世界,那么频域的“0”是什么呢?cos(0t)就是一个周期无限长的正弦波,也就是一条直线!所以在频域,0频率也被称为直流分量,在傅里叶级数的叠加中,它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。
2023-10-17 15:17:53 119
119 
提到傅里叶变换,你是不是又想起了大学课程里被它支配的恐惧。其实,傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。如果用方程写一部科学史,傅里叶变换必然拥有位置,它
2023-09-11 11:21:06 289
289 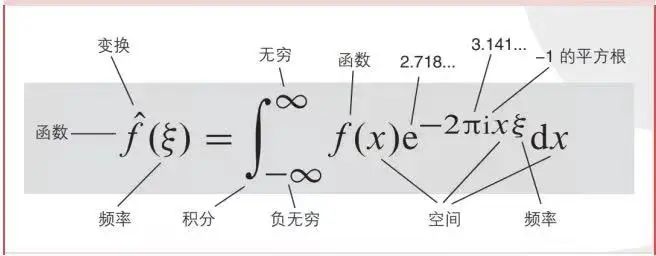
傅里叶变换和离散傅里叶变换的关系 傅里叶变换(Fourier Transform)是一种将时间域(或空间域)的信号转换为频率域(或波数域)的信号的数学工具。而离散傅里叶变换(Discrete
2023-09-07 17:04:15 330
330 如何由傅里叶变换推出傅里叶反变换 傅里叶变换和傅里叶反变换是信号处理和通信领域中的两个重要概念,是数字信号和连续信号的重要数学分析方法之一。傅里叶变换可以将时间域信号转化为频率域信号,而傅里叶反
2023-09-07 17:04:09 356
356 可以表示原始函数中不同频率的振幅和相位信息。傅里叶变换可以应用于信号处理、通信、图像处理、量子力学等领域。本文对傅里叶变换中的一些重要公式进行总结和详细说明。 1. 傅里叶级数公式 傅里叶级数是傅里叶变换的前身,它适
2023-09-07 16:53:08 3859
3859 傅里叶变换和反变换公式 傅里叶变换和反变换在信号处理领域中被广泛应用。傅里叶变换是将一个时域信号转换为频域信号的过程,而傅里叶反变换则是将一个频域信号转换为时域信号的过程。这篇文章将详细讲解
2023-09-07 16:53:04 2916
2916 傅里叶级数展开的求解方法 傅里叶级数展开是一种将周期函数分解为一系列正弦或余弦函数的方法。该方法在数学、物理、信号处理、图像处理和工程等领域中得到广泛应用。本文将探讨傅里叶级数展开的定义、求解方法
2023-09-07 16:47:58 603
603 傅里叶级数有时移特性 傅里叶级数是指将周期函数分解为一系列正弦函数和余弦函数的和的表达式。它得名于法国数学家傅里叶,被广泛应用于信号处理、图像处理、噪声分析等领域。傅里叶级数的最重要的特征之一
2023-09-07 16:43:50 309
309 傅里叶变换和傅里叶逆变换的关系 傅里叶变换和傅里叶逆变换是信号处理领域中极具重要性的数学工具,它们被广泛应用于很多领域,例如音频、图像处理、通信等。 傅里叶变换是将一个信号在时域(即时间或空间)上
2023-09-07 16:43:47 581
581 三角级数和傅里叶级数的区别 三角级数和傅里叶级数是数学中两个重要的概念。它们都涉及到无穷级数,但它们的应用和本质有所不同。在本文中,我们将深入探讨这两个概念的区别和应用,希望能够帮助读者更好地理
2023-09-07 16:43:42 283
283 傅里叶变换和傅里叶级数的关系 傅里叶变换和傅里叶级数都是数学领域中非常重要的概念和理论,这两者之间存在着密不可分的联系。在本文中,我们将从多个角度来深入探讨傅里叶变换和傅里叶级数的关系,以便更好
2023-09-07 16:39:01 960
960 正弦函数的傅里叶变换 正弦函数是数学中一种广泛应用的基本函数,其在傅里叶分析中也是具有重要作用的函数之一。在实际应用中,我们常常需要将正弦函数进行傅里叶变换,以求得自变量函数在频域上的表现,从而更好
2023-09-07 16:35:07 836
836 傅氏变换和傅里叶变换的区别联系 傅氏变换和傅里叶变换是信号处理中常用的两种变换方法,它们有着不同的作用和特点。傅氏变换主要应用于连续时间信号的频域分析,而傅里叶变换则主要用于离散时间信号的频域分析
2023-09-07 16:35:05 195
195 傅里叶变换的意义和性质 为什么万物皆可傅里叶 傅里叶变换是一种通过将时间域上的函数转换为频率域上的函数,来分析信号的方法。它是在18世纪末由法国数学家约瑟夫·傅里叶所发明的,它的形式为一个积分
2023-09-07 16:19:02 385
385 傅里叶变换的数学意义 傅里叶变换是一种数学工具,它是一种将一个函数在一个频域转换为另一个函数在另一个频域中的操作。傅里叶变换起源于1807年,由法国数学家让·巴蒂斯特·约瑟夫·傅里叶提出,它是一种将
2023-09-07 16:18:51 148
148 具有很多有用的性质,因此在信号处理、通信和控制等领域中得到了广泛的应用。下面就来介绍傅里叶变换的十大公式和性质。 一、傅里叶正变换 一般形式: $F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt$ 其中,$f(t)$为时域信号,$F(\ome
2023-09-07 16:14:36 1210
1210 傅里叶变换的意义和理解 傅里叶变换是一种将一个信号在频域中进行分解的数学工具,它将一个信号分解为不同频率的正弦和余弦波的叠加。傅里叶变换的基本概念源于法国数学家约瑟夫·傅里叶,而其在现代通信、图像
2023-09-07 16:08:42 3549
3549 由信号的分解可知,周期信号f(t)在区间(t0,t0+T)可以展开成在完备正交信号空间的无穷级数。如果完备的正交函数集是三角函数集或指数函数集,那么,周期信号所展开的无穷级数就分别称为"三角型傅里叶级数"或"指数型傅里叶级数",统称傅里叶级数。
2023-08-23 15:21:22 195
195 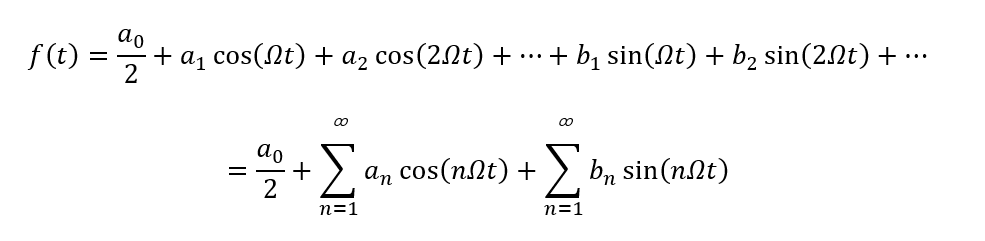
傅里叶级数——采用三角函数系(互为正交函数)进行正交展开
2023-08-09 15:00:31 304
304 
谈到傅里叶级数,我们先要谈傅里叶变换。笼统来说,傅里叶变换的目的将一个信号从时域变换到频域进行分析,原因是很多在时域内看不见的特性在频域内能很清楚地得到。
2023-08-09 11:51:02 610
610 
但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一长串公式,让人云山雾罩。
2023-07-17 10:18:49 199
199 
根据时域信号的表现的不同特点(连续或离散,周期或非周期),傅里叶分析有不同的类型,不同的叫法以示区别,如图1所示。
2023-06-11 16:22:54 470
470 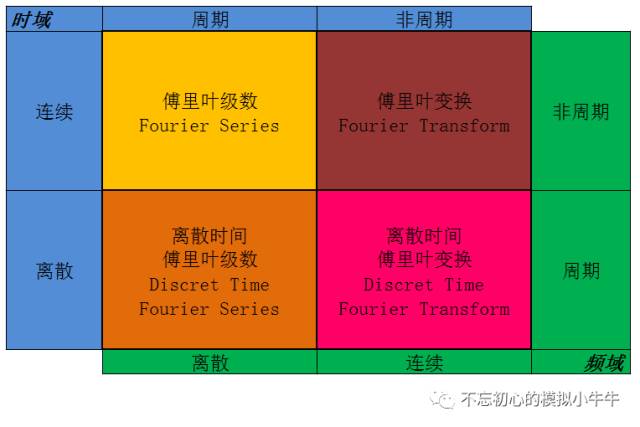
傅里叶级数真的优雅,一般书本上的习题也都是三角波、矩形波,积分起来相对容易。
2023-05-25 11:19:52 762
762 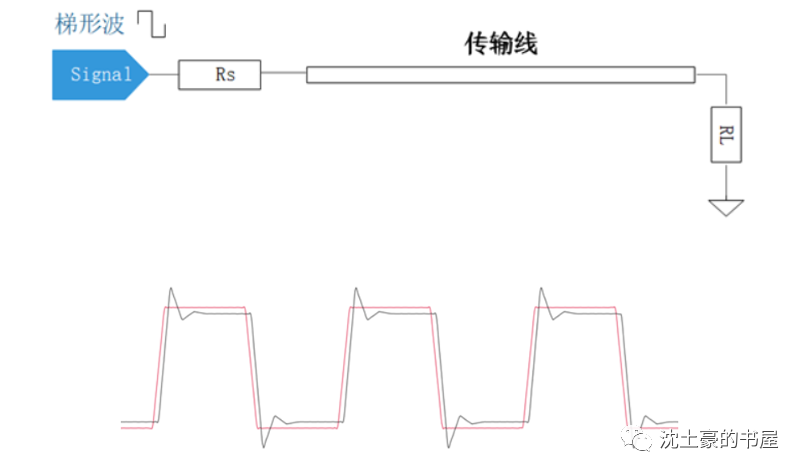
拉普拉斯变换与傅里叶变换的关系.ppt拉普拉斯变换与傅里叶变换的关系拉氏变换的引出,是针对 &
2009-09-16 08:42:31
了解傅里叶级数在电路分析和傅里叶级数方程中的重要性,同时深入了解该分析工具的工作原理。 这 傅里叶级数 是一个强大的工具,可以表达 非正弦周期波形 作为 正弦波形。在本文中,我们将首先通过介绍傅里叶
2023-01-27 14:11:00 587
587 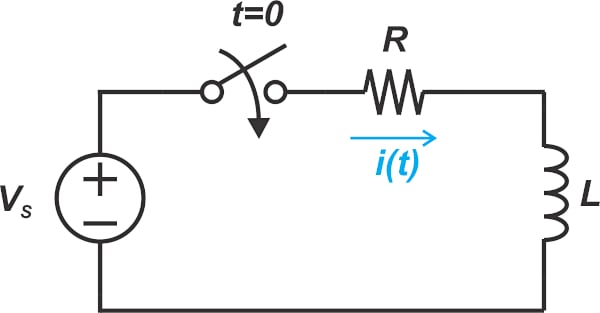
傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。
2023-01-12 11:17:15 1876
1876 傅里叶变化只能对能量有限的信号进行变换(也就是可以收敛的信号),无法对能量无限的信号进行变换(无法收敛),因此,拉普拉斯应运而生,在原先的傅里叶变换公式中乘以一个衰减因子,使得无限能量的信号也能进行时频变换。
2022-11-28 11:00:23 1013
1013 文章从实际出发,讲述了什么是傅里叶变换,它的理论基础以及Numpy和OpenCV实现傅里叶和逆傅里叶变换,并最终用高通滤波和低通滤波的示例。
2022-07-05 16:04:20 1025
1025 傅里叶逆变换就是傅里叶变换的逆过程,在F(ω)和求内积的时候,F(ω)只有t时刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t时刻上的分量叠加起来,叠加的结果就是f(t)在t时刻的值,这就回到了我们观察信号最初的时域。
2022-03-14 10:14:19 3669
3669 FTIR傅里叶红外光谱仪产品说明(英文版)
2021-11-05 17:24:04 1
1 从傅里叶级数、傅里叶变换推出拉普拉斯变换。
2021-06-23 16:25:27 5437
5437 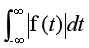
原信号的不同类型,傅里叶变换可以分为四种类别: (1)非周期性连续信号傅里叶变换 (2)周期性连续信号傅里叶级数 (3)非周期性离散信号离散时域傅里叶变换 (4)周期性离散信号离散傅里叶变换 快速傅里叶变换(FFT),是利用计算机计算离散傅里叶
2020-11-09 16:52:40 12009
12009 
的相关运算已经非常成熟,有现成函数可以调用。对于绝大部分只需用好傅里叶变换的同学,重要的不是去记那些枯燥的公式,而是解傅里叶变换的含义及意义。 本文试图不用一个数学公式,采用较为通俗的语言深入浅出的阐述傅里叶变
2020-10-10 18:03:17 21666
21666 
“傅里叶”这个名字,我相信对很多人来说并不陌生。尤其是理工科的童鞋,对这三个字应该是如雷贯耳。
2020-09-16 11:06:48 4144
4144 
了解周期序列的傅里叶级数及性质,掌握周期卷积过程
理解离散傅里叶变换及性质,掌握圆周移位、共轭对称性,掌握圆周卷积、线性卷积及两者之间的关系件
2020-04-13 08:00:00 1
1 法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的)
2020-04-04 17:17:00 2514
2514 
傅里叶,Jean Baptiste Joseph Fourier(简·巴普蒂斯·约瑟夫·傅里叶,1768/3/21-1830/5/16,法国男爵,数学家、物理学家,图1-1),这位大魔王是很多理工科人的噩梦。
2019-12-06 15:36:00 77
77 本文档的主要内容详细介绍的是数字信号处理教程之DFT和FFT处理的学习课件免费下载包括了:1.离散傅里叶变换,2.与傅里叶变换的关系,3.与傅里叶级数的关系,4.DFT 窗效应,6.快速傅里叶变换。
2019-11-13 17:08:16 12
12 但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一长串公式,让人云山雾罩。
2019-06-29 09:34:34 118041
118041 
最近在看《信号与系统》,连续傅里叶级数和离散傅里叶级数中,离散傅里叶级数的谐波信号种类是有限的,而连续时间信号的傅里叶级数的谐波信号就有无数个,这个让我很不解。
2019-06-01 09:28:49 1703
1703 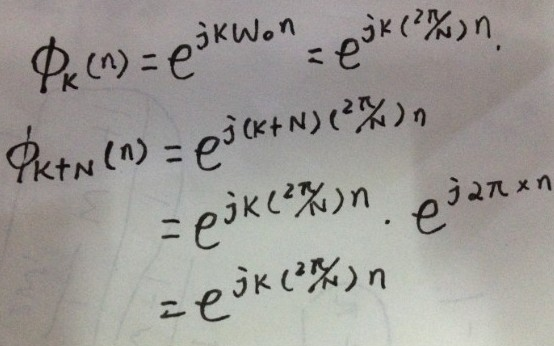
傅里叶变换是数字信号处理领城种很重要的算法。傅里叶表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理的傅里叶变换算法利用直接测量到的原始信号,以累加方式来计算该
2019-04-30 08:00:00 2
2 连续时间信号的频域分析,是本课程最为重要的内容之一,也是考试的重点。包括三方面内容:周期信号的傅里叶级数、非周期信号的傅里叶变换、时域抽样。本文对前两个内容进行较为详细的总结。
2018-05-19 09:15:28 50134
50134 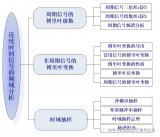
主要内容:
1.三角函数形式的傅氏级数
2.指数函数形式的傅氏级数
3.两种傅氏级数的关系
4.频谱图
5.函数的对称性与傅里叶级数的关系
6.周期信号的功率
7.傅里叶有限级数与最小方均误差
2018-03-05 11:31:50 3
3 本文研究的目的是检测不同光照下纺织工业中织布的瑕疵,不同光照下的织布图像清晰度不同,但却都非常有周期性,有方向性。所以本文提出了一种基于傅里叶极坐标变换的方法:该方法将图像在频域内的频谱能量转化到
2017-12-12 18:35:17 1
1 周期信号的频谱分析——傅里叶级数
2017-12-06 14:27:04 2
2 典型周期信号的傅里叶级数
2017-12-06 14:25:17 1
1 一种积分变换,它来源于函数的傅里叶积分表示。积分称为ƒ 的傅里叶积分。拉普拉斯变换是工程数学中常用的一种积分变换,又名拉氏变换。拉氏变换是一个线性变换,可将一个有参数实数t(t≥ 0)的函数转换为一个参数为复数s的函数。
2017-12-05 19:10:02 83345
83345 
小波与傅里叶分析基础
有需要的朋友下来看看
2015-12-30 15:33:42 1
1 傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,我保证这篇文章和你以前看过的所有文章都不同,让大家了解傅里叶变换。
2014-05-29 09:33:36 49120
49120 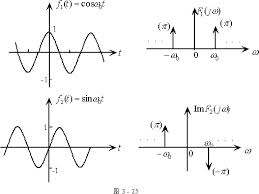
傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,我保证这篇文章和你以前看过的所有文章都不同,让大家了解傅里叶变换。
2014-05-27 09:11:32 250363
250363 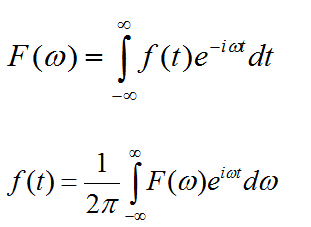
电子发烧友网站提供《小波与傅里叶分析基础_中文版_.txt》资料免费下载
2012-07-07 13:32:19 16
16 向读者展示傅里叶分析和小波的许多基础知识以及在信号分析方面的应用。全书分为8章和3个附录,第0章是学习第1章至第7章的准备知识,即内积空间;第1章讲解傅里叶级数的基础知识
2011-07-14 11:25:20 195
195 摘要用球面波照明物体的自由空间菲涅耳衍射3实现分数(p1)级傅里叶逆变换,提供了分数傅里叶 逆变换无透镜光学实现的模式及其参量选择的法则,对光学信息处理具有实用价值.计算机模拟实验证明了结论的可靠与可行. 关键词:分数级,傅里叶,逆变换
2011-02-23 09:35:17 29
29 连续信号的傅里叶分析:信号分析就是要研究信号如何表示为各分量的叠加,并从信号分量的组成情况去考察信号的特性。由上一章的讨论可知,连续时间信号可以表示为基本信号
2009-10-04 09:21:54 35
35 序列的傅里叶变换(DTFT) :DTFT:Discrete-time Fourier transform为研究离散时间系统的频率响应作准备,从抽样信号的傅里叶变换引出:二.傅氏变换、拉氏变换、z变换的关系1. 三
2009-09-30 19:38:25 36
36 非周期信号的傅里叶变换
前面已讨论了周期非正弦信号的傅里叶级数展开,下面来分析非周期信号的傅里叶变换。当周期
2009-07-27 10:23:30 7992
7992 非正弦周期信号的傅里叶级数分解
前面章节中已对直流电路与正弦交流电路的分析计算方法作了详细介绍,当电路的激励
2009-07-27 10:20:16 21863
21863 快速付里叶变换:一、快速付里叶变换FFT有 限 长 序 列 通 过 离 散 傅 里 叶 变 换 (D F T) 将 其 频 域 离 散 化 成 有 限 长 序 列 . 但 其 计算 量 太 大, 很 难 实 时 地 处
2009-07-25 11:43:24 76
76 1)付里叶变换的四种形式(2)离散付里叶级数(3)离散付里叶变换(4)离散付里叶变换的有关性质(5)频率抽样理论(6)离散付里叶变换的应用(7)DFT逼近连
2009-07-25 11:42:30 14
14 Z变换与拉氏变换、傅氏变换的关系:一.Z变换与拉氏变换的关系1.理想抽样信号的拉氏变换设为连续信号, 为其理想抽样信号,则
2.Z变换与拉氏变换的关系( S、Z平面映
2009-07-25 10:32:44 40
40 离散傅里叶变换及其快速算法离散傅里叶变换 (Discrete Fourier Transform,DFT)是时间函数是离散的,而且频谱函数也是离散的变换。3. 1 讨论周期序列的 傅里叶级数及其性质。
2008-10-30 12:54:54 33
33 三角函数形式的傅氏级数 指数函数形式的傅氏级数两种傅氏级数的关系 频谱图函数的对称性与傅里叶级数的关系周期信号的功率傅里叶
2008-08-05 12:22:02 38
38 从本章开始由时域转入变换域分析,首先讨论傅里叶变换。傅里叶变换是在傅里叶级数正交函数展开的基础上发展而产生的,这方面的问题也称为傅里叶分析(频域分析)。将信号
2008-08-05 11:49:37 50
50










![]() 趋于零。也就是说,一个非周期函数会通过傅里叶变换被描述成连续的正弦函数的组合,即在频域上连续。基于这个思想,傅里叶级数即将演化成傅里叶变换。
趋于零。也就是说,一个非周期函数会通过傅里叶变换被描述成连续的正弦函数的组合,即在频域上连续。基于这个思想,傅里叶级数即将演化成傅里叶变换。





 电子发烧友App
电子发烧友App










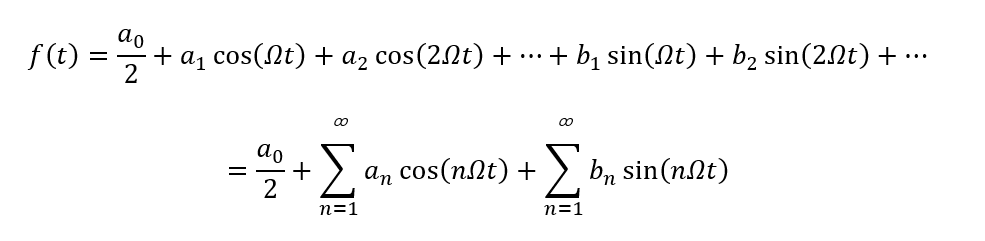














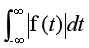








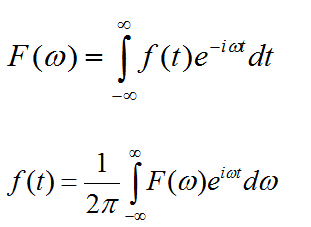










评论