在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
控制点包含三种比较简单的PID控制算法,分别是:增量式算法,位置式算法,微分先行。 这三种PID算法虽然简单,但各有特点,基本上能满足一般控制的大多数要求。
PID算法简介
在智能车竞赛中,要想让智能车根据赛道的不断变化灵活的行进,PID算法的采用很有意义。
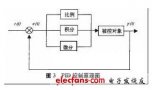
首先必须明确PID算法是基于反馈的。一般情况下,这个反馈就是速度传感器返回给单片机当前电机的转速。简单的说,就是用这个反馈跟预设值进行比较,如果转速偏大,就减小电机两端的电压;相反,则增加电机两端的电压。
顾名思义,P指是比例(Proportion),I指是积分(Integral),D指微分(Differential)。在电机调速系统中,输入信号为正,要求电机正转时,反馈信号也为正(PID算法时,误差=输入-反馈),同时电机转速越高,反馈信号越大。要想搞懂PID算法的原理,首先必须先明白P,I,D各自的含义及控制规律:
² 比例P:比例项部分其实就是对预设值和反馈值差值的发大倍数。举个例子,假如原来电机两端的电压为U0,比例P为0.2,输入值是800,而反馈值是1000,那么输出到电机两端的电压应变为U0+0.2*(800-1000)。从而达到了调节速度的目的。显然比例P越大时,电机转速回归到输入值的速度将更快,及调节灵敏度就越高。从而,加大P值,可以减少从非稳态到稳态的时间。但是同时也可能造成电机转速在预设值附近振荡的情形,所以又引入积分I解决此问题。
比例控制理解
首先是比例控制。比例控制就好比是通过水桶往水缸加水或者从水缸舀水。假设我们需要把水平面稳定在A平面,而实际水平面在B平面,那么水平面差值Err=A-B,那这个时候我们需要往里面加水的量就是Kp*Err,Kp就是我们的比例控制系数。
如果A》B,Err为正,就往水缸里面加水;如果A《B,Err为负,就从水缸里面舀水出来。那么只要预期水平面和实际水平面有差值,我们都会通过水桶去加减水来调整系统。同时Kp的大小也有对系统的性能有影响。如果Kp的值比较大,优点是从B平面达到A平面的速度快,缺点是在B平面已经接近A平面的时候系统会产生比较大的震荡。如果Kp的值比较小,优点是B平面在接近A平面的时候系统震荡小,缺点是从B平面达到A平面的速度慢。
这里也许有人会有疑问,如果这里把比例控制系数Kp直接设置成1,然后加水的量直接为Err=A-B不就可以了。然而实际上很多系统是做不到这点的。比如温度控制系统,实际温度为10度,我要通过加热把温度提升到40度,这里难道我们能一次性准确的给系统加30度?显然这是做不到的。那么比例控制的最终结果是Err的值趋向于0。比例控制部分公式如下图:
² 积分I:顾名思义,积分项部分其实就是对预设值和反馈值之间的差值在时间上进行累加。当差值不是很大时,为了不引起振荡。可以先让电机按原转速继续运行。当时要将这个差值用积分项累加。当这个和累加到一定值时,再一次性进行处理。从而避免了振荡现象的发生。可见,积分项的调节存在明显的滞后。而且I值越大,滞后效果越明显。
积分控制理解
积分控制部分的作用主要是用来消除静差。那么积分是怎样来消除静差的呢?
比例控制只能尽量将Err调节到0,而微分的作用是将曲线的斜率控制到0则停止对其作用,但斜率为0的时候Err并不一定为0。
这个时候我们就需要积分来起作用了。我们知道曲线的积分相当于曲线与x轴围出来的面积。如下图,积分作用的目的是使红色部分的面积和蓝色部分的面积的和为0,那么即使系统在比例控制和微分控制部分已经趋于稳定,只要Err不为0就会存在静差,只要存在静差那么积分就会对系统产生影响,直到系统的Err值为0。那么这样我们的PID控制在理论上就可以达到一个非常精确的控制效果。
来看看我们的积分公式部分:
² 微分D:微分项部分其实就是求电机转速的变化率。也就是前后两次差值的差而已。也就是说,微分项是根据差值变化的速率,提前给出一个相应的调节动作。可见微分项的调节是超前的。并且D值越大,超前作用越明显。可以在一定程度上缓冲振荡。比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,这样,具有比例+微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。
微分控制理解
然后我们先看看微分控制。在我们的比例控制的作用下,Err是开始减小的(假设一开始预期水平面A大于实际水平面B,也就是说Err是一个正值),那么也就是说Err随时间是一条斜率小于0的曲线,那么在周期时间内,Err越大,微分的绝对值越大,那么也就对Err的减小速度是起到抑制的作用的,直到最后斜率为0微分才会停止作用。微分公式如下:
那么随着微分的影响,Err曲线的斜率最终是趋向于0的,如下图:
二、参数调整一般规则
由各个参数的控制规律可知,比例P使反应变快,微分D使反应提前,积分I使反应滞后。在一定范围内,P,D值越大,调节的效果越好。各个参数的调节原则如下:
PID调试一般原则
a. 在输出不振荡时,增大比例增益P。
b. 在输出不振荡时,减小积分时间常数Ti。
c. 输出不振荡时,增大微分时间常数Td。
三、参数调整一般步骤
a.确定比例增益P
确定比例增益P 时,首先去掉PID的积分项和微分项,一般是令Ti=0、Td=0,PID为纯比例调节。输入设定为系统允许的最大值的60%~70%,由0逐渐加大比例增益P,直至系统出现振荡;再反过来,从此时的比例增益P逐渐减小,直至系统振荡消失,记录此时的比例增益P,设定PID的比例增益P为当前值的60%~70%。比例增益P调试完成。
b.确定积分时间常数Ti
比例增益P确定后,设定一个较大的积分时间常数Ti的初值,然后逐渐减小Ti,直至系统出现振荡,之后在反过来,逐渐加大Ti,直至系统振荡消失。记录此时的Ti,设定PID的积分时间常数Ti为当前值的150%~180%。积分时间常数Ti调试完成。
c.确定积分时间常数Td
积分时间常数Td一般不用设定,为0即可。若要设定,与确定 P和Ti的方法相同,取不振荡时的30%。
d.系统空载、带载联调,再对PID参数进行微调,直至满足要求
找三个以上PID算法应用实例,结合实例明确参数调试的方法以及参数的意义,同时给小组成员做介绍
 电子发烧友App
电子发烧友App








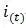
















评论