欧拉公式怎么写_欧拉公式的意义

　　欧拉公式将指数函数的定义域扩大到了复数域，建立和三角函数和指数函数的关系，被誉为“数学中的天桥”形式简单，结果惊人，欧拉本人都把这个公式刻在皇家科学院的大门上，看来必须好好推敲一番。

　　欧拉公式怎么写

　　欧拉公式有4条，我们一一的来了解一下：

　　（1）分式：

　　a＾r/（a-b）（a-c）+b＾r/（b-c）（b-a）+c＾r/（c-a）（c-b）

　　当r=0，1时式子的值为0

　　当r=2时值为1

　　当r=3时值为a+b+c

　　（2）复数

　　由e＾iθ=cosθ+isinθ，得到：

　　sinθ=（e＾iθ-e＾-iθ）/2i

　　cosθ=（e＾iθ+e＾-iθ）/2

　　此函数将两种截然不同的函数---指数函数与三角函数联系起来，被誉为数学中的“天桥”。

　　当θ=π时，成为e＾iπ+1=0 它把数学中最重要的e、i、π、1、0联系起来了。

　　（3）三角形

　　设R为三角形外接圆半径，r为内切圆半径，d为外心到内心的距离，则：

　　d＾2=R＾2-2Rr

　　（4）多面体

　　设v为顶点数，e为棱数，f是面数，则

　　v-e+f=2-2p

　　p为亏格，2-2p为欧拉示性数，例如

　　p=0 的多面体叫第零类多面体

　　p=1 的多面体叫第一类多面体

　　欧拉公式的意义

　　工程师一观点：

　　欧拉公式并没有把实数信号变为复数。首先想想欧拉公式是怎么推导出来的。欧拉发现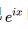的幂级数展开刚好是cos（x）和isin（x）的和，所以就有了

　　

　　接着来看傅立叶级数。傅立叶级数是把满足狄利克雷条件的周期函数表示为一系列具有不同频率的正弦与余弦函数的和。这些频率不同的三角函数是正交的，所以傅立叶级数就如同欧几里德空间里对向量进行正交分解一样，把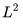空间里的平方可积函数分解到一组正交基上。

　　傅立叶级数可以表示成三角函数的和，也能表示成复指数函数的和，原因就是有欧拉公式在二者之间作为桥梁。两种表示方法都是可行的，只是人们发现复指数函数的表达方式在计算上更为便捷。

　　实信号的傅立叶系数，在下标互为相反数的系数是共轭复数，所以它们的和依然是实数。也就是说，实信号变换以后仍然是实数。

　　至于你最想知道的，这么做的意义是什么，在刚开始学信号与系统的时候，是很难理解的。我当时也一直想知道，各种变换的意义是什么。比如我思考了很久卷积的意义是什么，后来才发现，卷积这种运算没有比较明显的直观含义。后来用多了用熟练了就明白它的作用了。信号学到后面，再学实变函数和泛函分析之类的，就不能去多想意义是什么，那些抽象的东西，真的没有什么直观的意义。

　　工程师二观点：

　　信号变换的核心是傅立叶级数，用一组正交基sin/cos函数（信号）合成表示原信号。分解得到的一系列sin/cos函数（信号）经过欧拉公式变换为复数形式，一个复数就能同时表示分解的信号的分量的相位和幅度，其中相位表示cos/sin起振的角度，幅度是信号强度。

　　简而言之，就是傅氏级数就是信号分解，将复杂信号分解简单的正交余弦信号，傅立叶变换得到各个信号分量的幅度与起振角度，引入欧拉公式变成复数是为了表示方便，后面对信号做运算也简单了很多，比如时域卷积经过傅立叶变换到频域就是相乘（逆变换回去也就是卷积的结果）（为何可以这样？参考傅立叶分析教材的严格证明），具体操作时候还要考虑一些细节比如周期信号、非周期信号、收敛不收敛，时间频率是否有限长等等。