惯性环节与延迟环节的区别:
惯性环节从输入开始时刻就已有输出,仅由于惯性,输出要滞后一段时间才接近所要求的输出值;
延迟环节从输入开始后在0 ~ τ时间内没有输出,但t =τ之后,输出完全等于输入。
传递函数定义:
传递函数是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换(或z变换)与激励(即输入)量的拉普拉斯变换之比。记作G(s)=Y(s)/U(s),其中Y(s)、U(s)分别为输出量和输入量的拉普拉斯变换。传递函数是描述线性系统动态特性的基本数学工具之一,经典控制理论的主要研究方法——频率响应法和根轨迹法——都是建立在传递函数的基础之上。传递函数是研究经典控制理论的主要工具之一。
传递函数性质:
1、传递函数是一种数学模型,与系统的微分方程相对应。
2、是系统本身的一种属性,与输入量的大小和性质无关。
3、只适用于线性定常系统。
4、传递函数是单变量系统描述,外部描述。
5、传递函数是在零初始条件下定义的,不能反映在非零初始条件下系统的运动情况。
6、一般为复变量 S 的有理分式,即 n ≧ m。且所有的系数均为实数。
7、如果传递函数已知,则可针对各种不同形式的输入量研究系统的输出或响应。
8、如果传递函数未知,则可通过引入已知输入量并研究系统输出量的实验方法,确定系统的传递函数。
9、传递函数与脉冲响应函数一一对应,脉冲响应函数是指系统在单位脉冲输入量作用下的输出。
电压控制器的传递函数
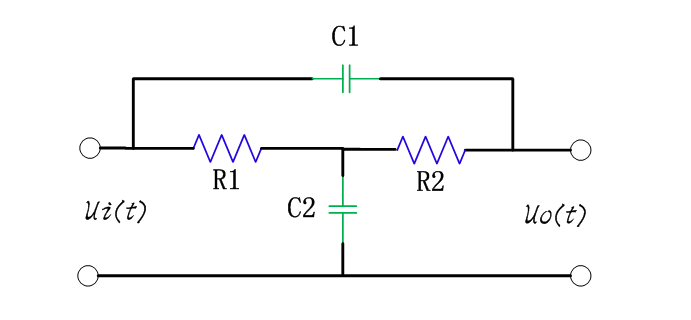
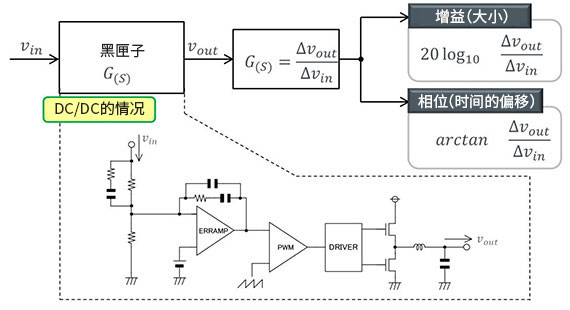
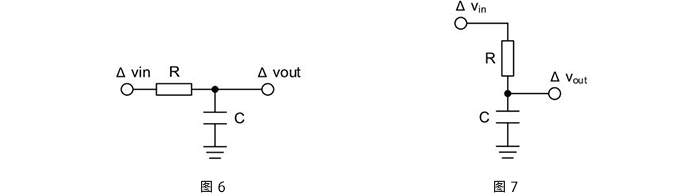
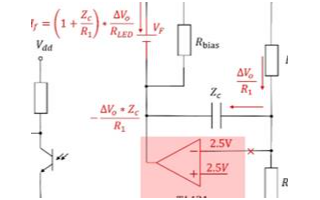
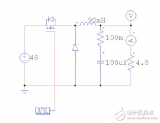
图所示为控制器(补偿网络)的原理图,它由运算放大器Z1(s)和Z2(s)组成。Z1(s)为运算放大器的输入阻抗,Z2(s)为反馈支路的阻抗。电压控制器的输入信号为误差信号为给定电压;k1为电压检测电路的传递函数,电压控制器的输出为uC(s)。可以证明电压控制器的传递函数为:图控制器(补偿网络)的原理图欢迎转载,信息来源维库电子市场网(www.dzsc.com)
图所示为控制器(补偿网络)的原理图,它由运算放大器Z1(s)和Z2(s)组成。Z1(s)为运算放大器的输入阻抗,Z2(s)为反馈支路的阻抗。电压控制器的输入信号为误差信号 为给定电压;k1为电压检测电路的传递函数,电压控制器的输出为uC(s)。可以证明电压控制器的传递函数为:
为给定电压;k1为电压检测电路的传递函数,电压控制器的输出为uC(s)。可以证明电压控制器的传递函数为:

传递函数应用:
1、 确定系统的输出响应。对于传递函数G(s)已知的系统,在输入作用u(s)给定后,系统的输出响应y(s)可直接由G(s)U(s)运用拉普拉斯反变换方法来定出。
2、分析系统参数变化对输出响应的影响。对于闭环控制系统,运用根轨迹法可方便地分析系统开环增益的变化对闭环传递函数极点、零点位置的影响,从而可进一步估计对输出响应的影响。
3、用于控制系统的设计。直接由系统开环传递函数进行设计时,采用根轨迹法。根据频率响应来设计时,采用频率响应法。
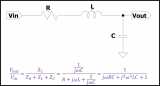
延迟环节的传递函数介绍:
其输出量与输入量变化形式相同,但要延迟一段时间
1、微分方程

2.传递函数与功能框

由拉氏变换延迟定理可得
上式表明,在延迟时间很小的情况下,延迟环节可用个小惯性环节来代替。

功能图框
3.举例
1)液压油从液压泵到阀控油缸间的管道传输产生的时间上的延迟。
2 )热量通过传导因传输速率低而造成的时间上的延迟。
3 )晶闸管整流电路,当控制电压改变时,由于晶闸管导通后即失控,要等到下一个周期开始后才能响应,这意味着,在时间上也会造成延迟(对单相全波电路,平均延迟时间to=5ms;对三相桥式,T=1.7ms)。
4 )各种传送带(或传送装置)因传送造成的时间上的延迟。
5 )从切削加工状况到测得结果之间的时间上的延迟
一钢板轧机如图,若轧机轧辊中心线到厚度测量仪的距离为d (这段距离无法避免),设轧钢的线速度为v,则测得实际厚度的时刻要比轧制的时刻延迟

 电子发烧友App
电子发烧友App








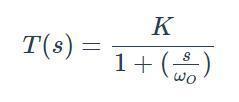
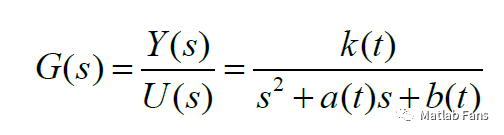
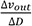
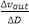
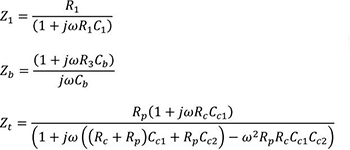


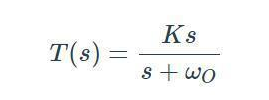
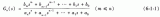

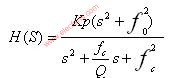
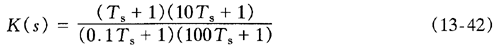
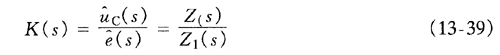










评论