一、最短路径简介
用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
二、动态规划求解问题的思路
在《算法导论》上,动态规划的求解过程主要分为如下的四步:
描述最优解的结构
递归定义最优解的值
按自底向上的方式计算最优解的值
由计算出的结果构造一个最优解
在利用动态规划求解的过程中值得注意的就是是否包含最优子结构,简单来讲就是一个问题的最优解是不是包含着子问题的最优解。利用求解子问题的最优解最后得到整个问题的最优解,这是利用动态规划求解问题的基本前提。
三、利用动态规划求解最短路径问题
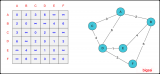
在解决这个问题的过程中,我其实是在尝试着使用不同的工具,首先我想对这种图处理,我使用了Gephi,Gephi是我在学习复杂网络的时候学会的一个工具,这个工具可以很方便的处理网络数据,能够动态的生成图的结构,下面是我用Gephi画出的图:

Gephi的另一个比较重要的工具就是可以在生成图的过程中,将图的数据导出,导出的数据可以方便的使用。
还是重点说说我是怎么利用动态规划的思想去求解这样的最短路径问题的:
1、描述最优解的结构
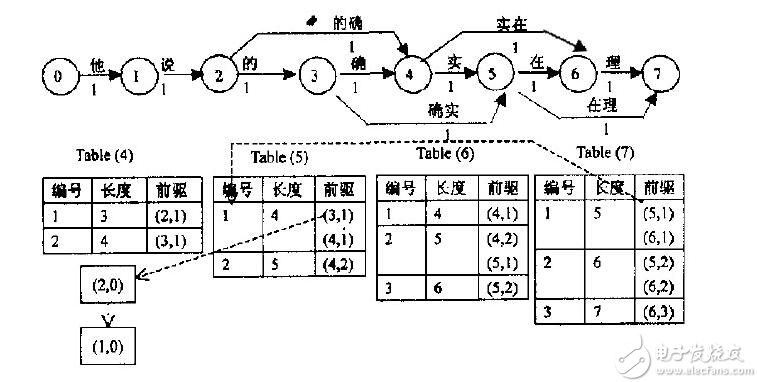
要使得从0到10的距离最短,令 为到第个节点的最短距离,则
为到第个节点的最短距离,则 用同样的方法可以求得
用同样的方法可以求得 等。
等。
2、递归定义最优解的值

其中表示与边有连接的节点,而且 。
。
3、按自底向上的方式计算每个节点的最优值
此时我们就得利用递归公式分别求解 ,这样最终便能得到最终的解。
,这样最终便能得到最终的解。
结果为:

最短路径解决方法
用于解决最短路径问题的算法被称做“最短路径算法”, 有时被简称作“路径算法”。 最常用的路径算法有:
Dijkstra算法
SPFA算法\Bellman-Ford算法
Floyd算法\Floyd-Warshall算法
Johnson算法
A*算法
所谓单源最短路径问题是指:已知图G=(V,E),我们希望找出从某给定的源结点S∈V到V中的每个结点的最短路径。
首先,我们可以发现有这样一个事实:如果P是G中从vs到vj的最短路,vi是P中的一个点,那么,从vs沿P到vi的路是从vs到vi的最短路。
JAVA实现:
[java] view plain copypackage org.algorithm.dynamicprogramming;
import java.io.BufferedReader;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.IOException;
import java.io.Reader;
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
import java.util.Stack;
/**
* 利用动态规划求解最短路径问题
*
* @author dell
*
*/
public class CalMinDistance {
// 计算最短的距离
public static int[] calMinDistance(int distance[][]) {
int dist[] = new int[distance.length];
dist[0] = 0;
for (int i = 1; i 《 distance.length; i++) {
int k = Integer.MAX_VALUE;
for (int j = 0; j 《 i; j++) {
if (distance[j][i] != 0) {
if ((dist[j] + distance[j][i]) 《 k) {
k = dist[j] + distance[j][i];
}
}
}
dist[i] = k;
}
return dist;
}
// 计算路径
public static String calTheRoute(int distance[][], int dist[]) {
Stack《Integer》 st = new Stack《Integer》();
StringBuffer buf = new StringBuffer();
int j = distance.length - 1;
st.add(j);// 将尾插入
while (j 》 0) {
// int num = 0;
for (int i = 0; i 《 j; i++) {
if (distance[i][j] != 0) {
// num++;
if (dist[j] - distance[i][j] == dist[i]) {
st.add(i);
}
}
}
j = st.peek();
}
while (!st.empty()) {
buf.append(st.pop()).append(“--》”);
}
return buf.toString();
}
// 读取文件
@SuppressWarnings(“resource”)
public static int[][] readTheFile(File f) {
Reader input = null;
try {
input = new FileReader(f);
} catch (FileNotFoundException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
BufferedReader buf = null;
buf = new BufferedReader(input);
List《String》 list = new ArrayList《String》();
try {
String str = buf.readLine();
while (str != null) {
list.add(str);
str = buf.readLine();
}
} catch (IOException e) {
// TODO Auto-generated catch block
e.printStackTrace();
}
Iterator《String》 it = list.iterator();
int distance[][] = new int[11][11];
while (it.hasNext()) {
String str1[] = it.next().split(“,”);
int i = Integer.parseInt(str1[0]);
int j = Integer.parseInt(str1[1]);
distance[i - 1][j - 1] = Integer.parseInt(str1[2]);
}
return distance;
}
public static void main(String args[]) {
// 读文件
File f = new File(“D:” + File.separator + “distance_1.csv”);
int distance[][] = readTheFile(f);
int dist[] = calMinDistance(distance);
System.out.println(“最短路径长度为:” + dist[distance.length - 1]);
System.out.println(“最短路径为:” + calTheRoute(distance, dist));
}
}
 电子发烧友App
电子发烧友App


















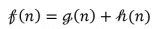












评论