双管自激振荡电路设计分析

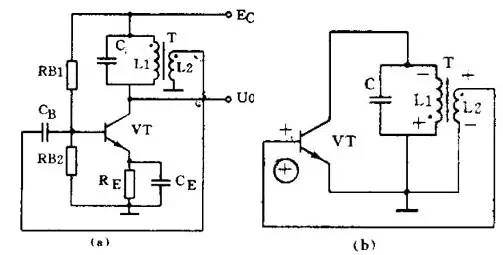
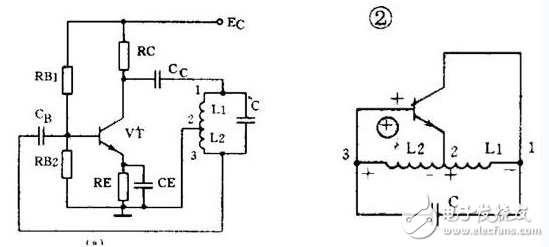
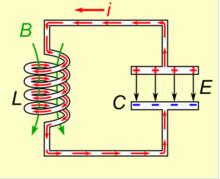
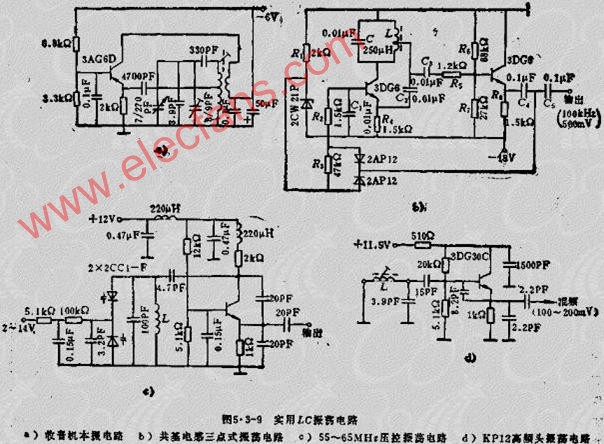
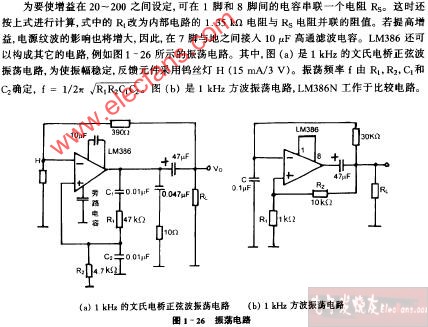
　　自激振荡常用于正弦波发生器、交流控制信号等。自激振荡的应用于许多电路，如正弦波振荡器广泛用于各种电子设备中，在模拟电子技术中属于必不可少的一种元件。它是一种不需要输入信号控制就能自动地将直流能量转换为特定频率和振幅的正弦交变能量的电路。常见的自激振荡电路如RC振荡电路和LC振荡电路。RC振荡电路中，RC网络既是选频网络又是正反馈电路中的一部分。该电路特点是电路简单，经济但稳定性不高。相比之下还有LC振荡电路，LC振荡器的选频网络是LC谐振回路，它们的振荡频率都比较高，LC振荡电路的特点是频率范围宽，容易起振，但频率稳定性不高。

　　自激振荡的概念和形成条件以及自激振荡的稳定

　　自激振荡就是电路中有一部分信号从输出端反馈到输入端，反馈回的信号加强了电路的振荡。下面以常见的负反馈放大电路和正反馈放大电路为例解释一下自激振荡

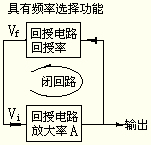
　　比较图1和图2就可以明显地看出负反馈放大电路和正反馈振荡电路的区别了。由于振荡电路的输入信号iX=0，所以iX=fX。由于正、负号的改变，有反馈的放大倍数为

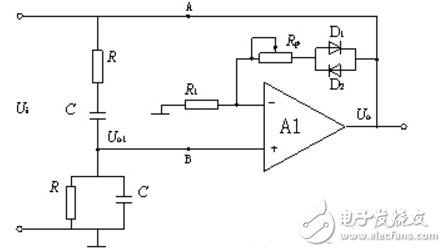
　　正弦波振荡器的名称一般由选频网络来命名。正弦波发生电路组成有：放大电路、正反馈电路、选频网络、稳幅电路。为了产生正弦波，必须在放大电路里加入正反馈，因此放大电路和正反馈网络是振荡电路的最主要部分。但是，这样两部分构成的振荡器一般得不到正弦波，这是由于很难控制正反馈的量。如果正反馈量大，则增幅，输出幅度越来越大，最后由三极管的非线性限幅，这必然产生非线性失真。反之，如果正反馈量不足，则减幅，可能停振，为此振荡电路要有一个稳幅电路。为了获得单一频率的正弦波输出，应该有选频网络，选频网络往往和正反馈网络或放大电路合而为一。选频网络由R、C和L、C等电抗性元件组成。

　　正弦波振荡器广泛用于各种电子设备中，在模拟电子技术中属于必不可少的一种元件。它是一种不需要输入信号控制就能自动地将直流能量转换为特定频率和振幅的正弦交变能量的电路。正弦波振荡器是自激振荡的一个非常重要的应用。根据傅里叶级数的定义可以知道，任何周期性的激励电压都可以分解成许多不同频率的正弦时间函数之和，再根据自激振荡的原理，只有频率为一特定值0f的正弦波才能够通过电路的正反馈系统（反馈系统本身可能为负反馈系统，但由于电容的存在，反馈信号与输入信号同相）增强自身，其余频率的信号都逐渐衰减到零。由于想要的正弦波信号为一稳定信号，因此在正弦波振荡器中加入了稳幅环节，其中，在分立元件组成的放大电路中，晶体管的非线性特性能够满足这个条件。最后当电路达到稳定时，AF=1。

　　生正弦波的条件与负反馈放大电路产生自激的条件十分类似。只不过负反馈放大电路中如图2所示是由于信号频率达到了通频带的两端，产生了足够的附加相移，从而使负反馈变成了正反馈如图3所示。在振荡电路中加的就是正反馈，振荡建立后只是一种频率的信号，无所谓附加相移。

　　（1）产生自激振荡必须同时满足两个条件：

　　1）幅度平衡条件|AF|=1

　　2）相位平衡条件（n=0，1，2，3···）其中，A指基本放大电路的增益（开环增益），F指反馈网络的反馈系数

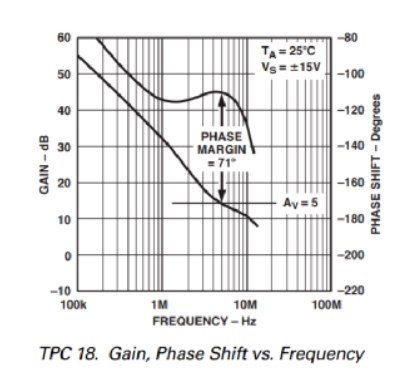
　　同时起振必须满足|AF|略大于1的起振条件基本放大电路必须由多级放大电路构成，以实现很高的开环放大倍数，然而在多级放大电路的级间加负反馈，信号的相位移动可能使负反馈放大电路工作不稳定，产生自激振荡。负反馈放大电路产生自激振荡的根本原因是A（环路放大倍数）附加相移。单级和两级放大电路是稳定的，而三级或三级以上的负反馈放大电路，只要有一定的反馈深度，就可能产生自激振荡，因为在低频段和高频段可以分别找出一个满足相移为180度的频率（满足相位条件），此时如果满足幅值条件|AF|=1，则将产生自激振荡。因此对三级及三级以上的负反馈放大电路，必须采用校正措施来破坏自激振荡，达到电路稳定工作目的。