霍夫曼压缩算法概述
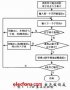
霍夫曼压缩算法的主要思想是用较少的比特表示出现频率较高的字符,用较多的比特表示出现频率较低的字符。如下图所示,

霍夫曼压缩算法实现
①读入完整的输入流,并转化为字符数组。
②计算每个字符出现的次数
③构建Huffman树
④构建编译表
⑤将单词查找树编码成比特输出串并写入到输出流
⑥将单词总数编码成比特输出串并写入到输出流
⑦使用编译表翻译每个输入字符
12345678
霍夫曼压缩算法节点的表示
private static final int R = 256; //字符为ASCII表示
private static class Node implements Comparable《Node》 {
private final char ch;
private final int freq;
private final Node left, right;
public Node(char ch, int freq, Node left, Node right) {
this.freq = freq;
this.ch = ch;
this.left = left;
this.right = right;
}
private boolean isLeaf() {
return left == null && right == null;
}
@Override
public int compareTo(Node that) {
return this.freq - that.freq;
}
}
123456789101112131415161718192021222324252627
构建Huffman单词查找树
构建初始有一堆没有父节点的节点,将它们放到最小队列中,这样对头总是freq为最小的那个节点。
从队列中找到freq最小的两个节点,创建一个它们的父节点,将三个节点归并成一个大节点,接着放入队列中,
循环往复直至队列中只剩一个节点。
/**
* @param freq 字符出现的次数
* @return
*/
private static Node buildTrie(char[] freq) {
MinPQ《Node》 pq = new MinPQ《Node》();
//初始化多个将构成一颗Huffman树的结点
for (char i = 0; i 《 R; i++) {
if (freq[i] 》 0) pq.insert(new Node(i, freq[i], null, null));
}
// special case in case there is only one character with a nonzero frequency
if (pq.size() == 1) {
if (freq[‘\0’] == 0) pq.insert(new Node(‘\0’, 0, null, null));
else pq.insert(new Node(‘\1’, 0, null, null));
}
//归并两个小树
while (pq.size() 》 1) {
Node left = pq.delMin();
Node right = pq.delMin();
Node parent = new Node(‘\0’, left.freq + right.freq, left, right); //创建连接子树的中间结点
pq.insert(parent);
}
return pq.delMin();
}123456789101112131415161718192021222324252627282930
将Huffman单词查找树转化成字节流写到压缩文件中
做如下规定:
中间结点写0;叶子结点写1,并在后面写结点上的字符。

/**
* 将单词查找树编码成比特输出串并写入到输出流
* 用前序遍历
*/
private static void writeTrie(Node x) {
if (x.isLeaf()) {
BinaryStdOut.write(true);
BinaryStdOut.write(x.ch);
return;
}
BinaryStdOut.write(false);
writeTrie(x.left);
writeTrie(x.right);
}
12345678910111213141516
将压缩文件中字节流转化为Huffman单词查找树
按写入时的规定解析字节流。
/**
* 读比特流,得出一颗单词查找树
*/
private static Node readTrie() {
if (BinaryStdIn.readBoolean()) { //读到1,说明是叶子结点
return new Node(BinaryStdIn.readChar(), 0, null, null);
}
//读到的是0,说明是中间结点,需要递归直到读到1为止
Node left = readTrie();
Node right = readTrie();
return new Node(‘\0’, 0, left, right);
}
123456789101112131415
构建编译表
构建编译表st,索引为字符,值为路径(比特字符串)。
根据这张表,可以将源文件中的某个字符,压缩为更少bit表示的Huffman树上的路径。
private static void buildCode(String[] st, Node x, String s) {
if (!x.isLeaf()) {
buildCode(st, x.left, s + “0”);
buildCode(st, x.right, s + “1”);
} else {
st[x.ch] = s;
}
}
12345678910
压缩
/**
* 从输入流中读字节流,并将压缩后的结果写入输出流
*/
private static void compress() {
//①读入完整的输入流,并转化为字符数组
String s = BinaryStdIn.readString();
char[] input = s.toCharArray();
//②计算每个字符出现的次数,没有出现的就为0
char[] freq = new char[R];
for (int i = 0; i 《 input.length; i++) {
freq[input[i]]++;
}
//③构建Huffman树
Node root = buildTrie(freq);
//④构建编译表,将输入中的每个char值与一个比特字符串(即Huffman树上路径)相关联
String st[] = new String[R];
buildCode(st, root, “”);
//⑤将单词查找树编码成比特输出串并写入到输出流
writeTrie(root);
//⑥将单词总数编码成比特输出串并写入到输出流
BinaryStdOut.write(input.length);
//⑦使用编译表翻译每个输入字符
for (int i = 0; i 《 input.length; i++) {
String code = st[input[i]]; //code表示Huffman单词查找数上的路径
for (int j = 0; j 《 code.length(); j++) { //要一位一位地输出
if (code.charAt(j) == ‘1’) {
BinaryStdOut.write(true);
} else {
BinaryStdOut.write(false);
}
}
}
BinaryStdOut.close();
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
### 解压
/**
* 解压
* 读取压缩文件的比特流,
* 将比特流对应为路径在单词查找树上找,将找到的结点中的字符写出
*/
private static void expand() {
Node root = readTrie();
int N = BinaryStdIn.readInt(); //读出存在压缩文件中的字符串长度
for (int i = 0; i 《 N; i++) { //找出源文件中每个字符
Node x = root;
while (!x.isLeaf()) { //遍历,知道叶子结点
if (BinaryStdIn.readBoolean()) {
x = x.right;
} else {
x = x.left;
}
}
BinaryStdOut.write(x.ch);
}
BinaryStdOut.close();
}
 电子发烧友App
电子发烧友App






















评论