一、CRC简介
循环冗余校验(Cyclic Redundancy Check, CRC)是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数,主要用来检测或校验数据传输或者保存后可能出现的错误。它是利用除法及余数的原理来作错误侦测的。
在数据传输过程中,无论传输系统的设计再怎么完美,差错总会存在,这种差错可能会导致在链路上传输的一个或者多个帧被破坏(出现比特差错,0变为1,或者1变为0),从而接受方接收到错误的数据。为尽量提高接受方收到数据的正确率,在接收方接收数据之前需要对数据进行差错检测,当且仅当检测的结果为正确时接收方才真正收下数据。检测的方式有多种,常见的有奇偶校验、因特网校验和循环冗余校验等。
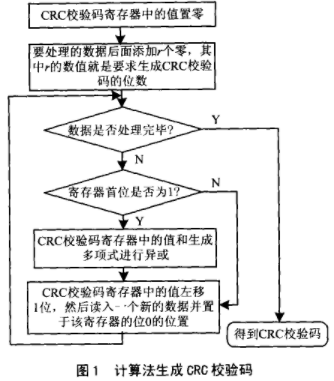
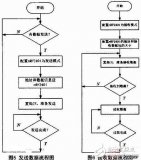
二、CRC硬件计算过程
1.设置CRC寄存器,并给其赋值FFFF(hex)。
2.将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或,并把结果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB补零,移出并检查LSB。
4.如果LSB为0,重复第三步;若LSB为1,CRC寄存器与多项式码相异或。
注意:该步检查LSB应该是右移前的LSB,即第3步前的LSB。
5.重复第3与第4步直到8次移位全部完成。此时一个8-bit数据处理完毕。
6.重复第2至第5步直到所有数据全部处理完成。7.最终CRC寄存器的内容即为CRC值。
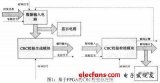
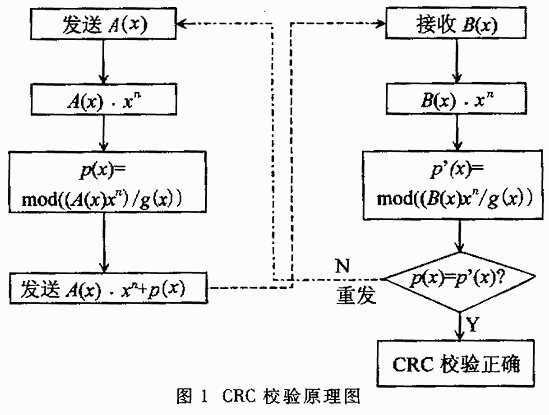
三、循环冗余校验码(CRC)的基本原理
在K位信息码后再拼接R位的校验码,整个编码长度为N位,因此,这种编码又叫(N,K)码。对于一个给定的(N,K)码,可以证明存在一个最高次幂为N-K=R的多项式G(x)。根据G(x)可以生成K位信息的校验码,而G(x)叫做这个CRC码的生成多项式。
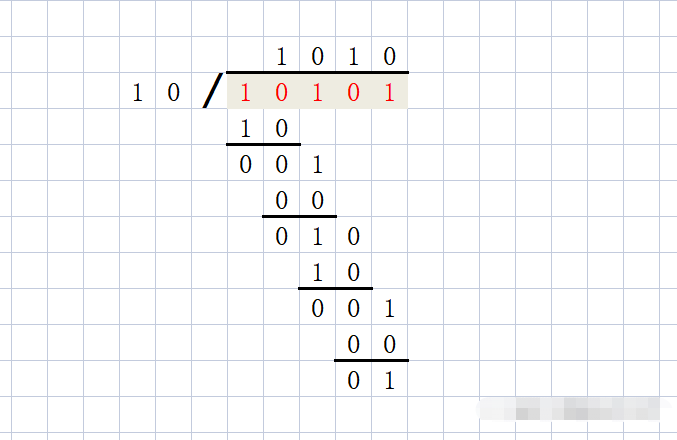
校验码的具体生成过程为:假设发送信息用信息多项式C(X)表示,将C(x)左移R位,则可表示成C(x)*2R,这样C(x)的右边就会空出R位,这就是校验码的位置。通过C(x)*2R除以生成多项式G(x)得到的余数就是校验码。
原理思维导图总结:


四、通信与网络中常用的CRC
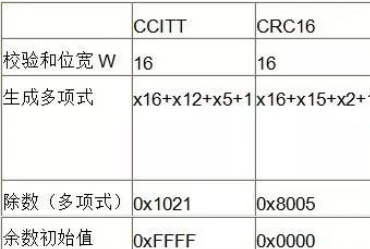
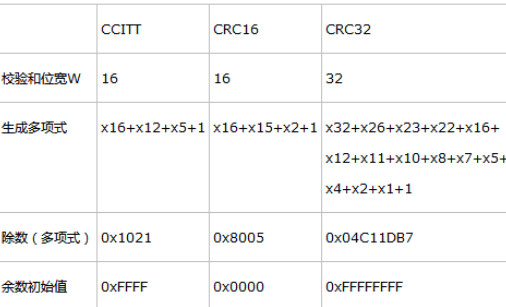
在数据通信与网络中,通常k相当大,由一千甚至数千数据位构成一帧,而后采用CRC码产生r位的校验位。它只能检测出错误,而不能纠正错误。一般取r=16,标准的16位生成多项式有CRC-16=x16+x15+x2+1 和 CRC-CCITT=x16+x15+x2+1。
一般情况下,r位生成多项式产生的CRC码可检测出所有的双错、奇数位错和突发长度小于等于r的突发错以及(1-2-(r-1))的突发长度为r+1的突发错和(1-2-r)的突发长度大于r+1的突发错。例如,对上述r=16的情况,就能检测出所有突发长度小于等于16的突发错以及99.997%的突发长度为17的突发错和99.998%的突发长度大于17的突发错。所以CRC码的检错能力还是很强的。这里,突发错误是指几乎是连续发生的一串错,突发长度就是指从出错的第一位到出错的最后一位的长度(但是,中间并不一定每一位都错)。
【例1】某循环冗余码(CRC)的生成多项式 G(x)=x3+x2+1,用此生成多项式产生的冗余位,加在信息位后形成 CRC 码。若发送信息位 1111 和 1100 则它的 CRC 码分别为_A_和_B_。由于某种原因,使接收端收到了按某种规律可判断为出错的 CRC 码,例如码字_C_、_D_、和_E_。(1998年试题11)
供选择的答案:
A:① lllll00 ② 1111101 ③ 1111110 ④ 1111111
B:① 1100100 ② 1100101 ③ 1100110 ④ 1100111
C~E:① 0000000 ② 0001100 ③ 0010111 ⑤ 1000110 ⑥ 1001111 ⑦ 1010001 ⑧ 1011000
解:
A:G(x)=1101,C(x)=1111 C(x)*23÷G(x)=1111000÷1101=1011余111
得到的CRC码为1111111
B:G(x)=1101,C(x)=1100 C(x)*23÷G(x)=1100000÷1101=1001余101
得到的CRC码为1100101
C~E:
分别用G(x)=1101对①~⑧ 作模2除: ① 0000000÷1101 余000 ② 1111101÷1101 余001
③ 0010111÷1101 余000 ④ 0011010÷1101 余000 ⑤ 1000110÷1101 余000
⑥ 1001111÷1101 余100 ⑦ 1010001÷1101 余000 ⑧ 1011000÷1101 余100
所以_C_、_D_和_E_的答案是②、⑥、⑧
【例2】计算机中常用的一种检错码是CRC,即 _A_ 码。在进行编码过程中要使用 _B_ 运算。假设使用的生成多项式是 G(X)=X4+X3+X+1, 原始报文为11001010101,则编码后的报文为 _C_ 。CRC码 _D_ 的说法是正确的。
在无线电通信中常采用它规定码字长为7位.并且其中总有且仅有3个“1”。这种码的编码效率为_E_。
供选择的答案:
A:① 水平垂直奇偶校验 ② 循环求和 ③ 循环冗余 ④正比率
B:① 模2除法 ②定点二进制除法 ③二-十进制除法 ④循环移位法
C:① 1100101010111 ② 110010101010011 ③ 110010101011100 ④ 110010101010101
D:① 可纠正一位差错 ②可检测所有偶数位错
③ 可检测所有小于校验位长度的突发错 ④可检测所有小于、等于校验位长度的突发错
E:① 3/7 ② 4/7 ③ log23/log27 ④ (log235)/7
解:从前面有关CRC的论述中可得出: A:③ 循环冗余 B:① 模2除法
C:G(x)=11011,C(x)=11001010101,C(x)*24÷G(x)=110010101010000÷11011 余0011
得到的CRC码为② 110010101010011
D:从前面有关通信与网络中常用的CRC的论述中可得出:④ 可检测所有小于、等于校验位长度的突发错
E:定比码又叫定重码,是奇偶校验的推广。在定比码中,奇数或偶数的性质保持不变,然而附加一种限制,每个字中1的总数是固定的。随用途之不同,定比码要求的附加校验位可能多于一个,但较之单一的奇偶校验将增加更多的检错能力。
所谓7中取3定比码,就是整个码字长度为7位,其中1的位数固定为3。所有128个7位代码(0000000~1111111)中只有1的位数固定为3的才是其合法码字。可以用求组合的公式求出其合法码字数为:C73=7!/(3!*(7-3)!)=7*6*5/(1*2*3)=35
编码效率=合法码字所需位数/码字总位数=(log235)/7
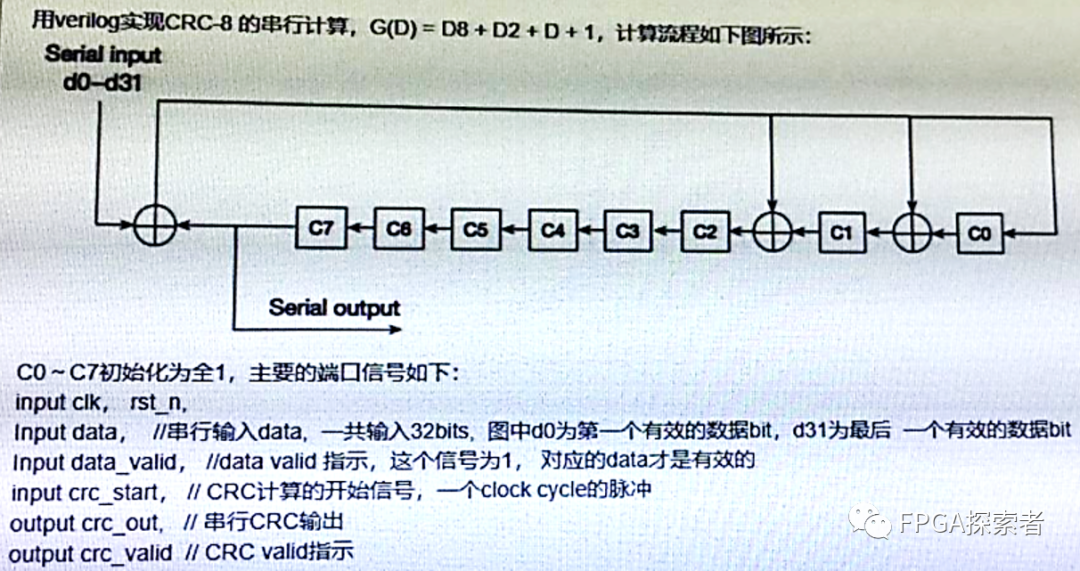
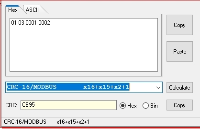
而对于CRC的实现有两种方式,分别为多项式和查表法。
 电子发烧友App
电子发烧友App








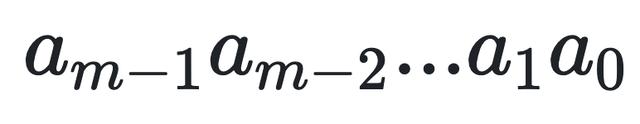


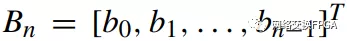


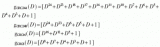
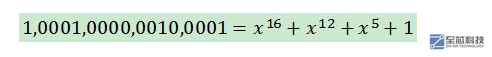


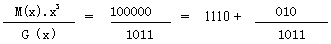











评论