巴特沃斯滤波器优缺点分析

　　滤波器的作用顾名思义就是过滤掉不需要的信号，它可以将有用的信号与噪声分离，提高信号的抗干扰性及信噪比，滤掉不感兴趣的频率成分等。巴特沃斯滤波器是三大原型模拟低通滤波器之一，今天小编要介绍的就是巴特沃斯滤波器。

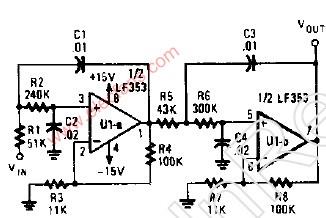
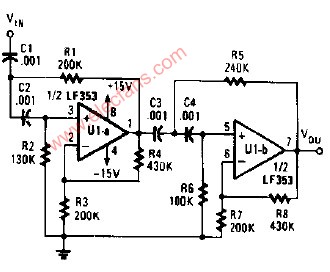
　　巴特沃斯滤波器电路

　　一阶巴特沃斯滤波器的衰减率为每倍频6分贝，每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。

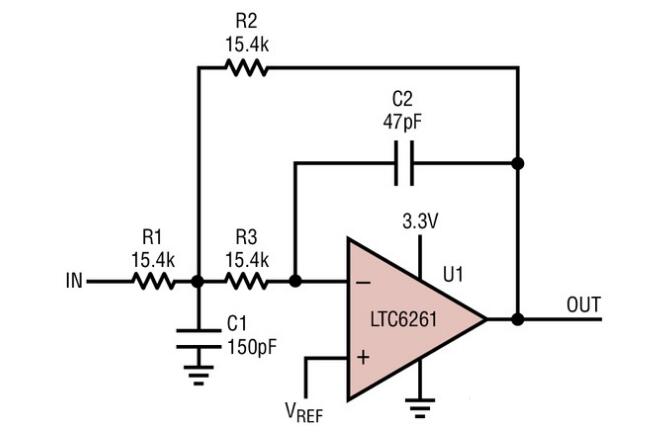
　　巴特沃斯滤波器原理

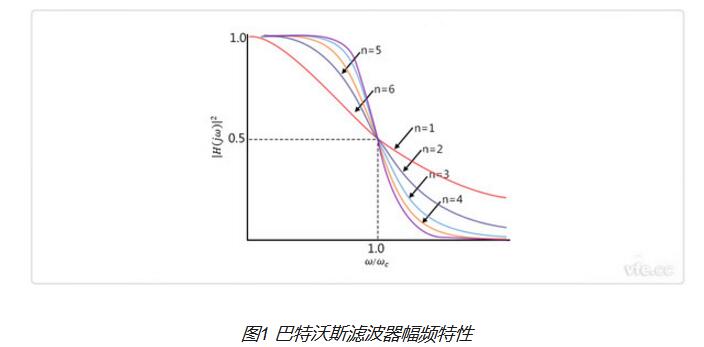
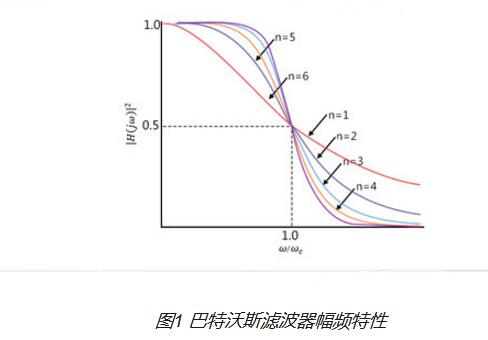
　　巴特沃斯型滤波器在现代设计方法设计的滤波器中，是最为有名的滤波器，由于它设计简单，性能方面又没有明显的缺点，又因它对构成滤波器的元件Q值较低，因而易于制作且达到设计性能，因而得到了广泛应用。其中，巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。

　　滤波器的截止频率的变换是通过先求出待设计滤波器的截止频率与基准滤波器的截止频率的比值M，再用这个M去除滤波器中的所有元件值来实现的，其计算公式如下：M=待设计滤波器的截止频率/基准滤波器的截止频率。

　　滤波器的特征阻抗的变换是通过先求出待设计滤波器的特征阻抗与基准滤波器的特征阻抗的比值K，再用这个K去乘基准滤波器中的所有电感元件值和用这个K去除基准滤波器中的所有电容元件值来实现的。

　　巴特沃斯低通滤波器简介

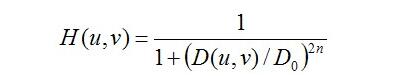
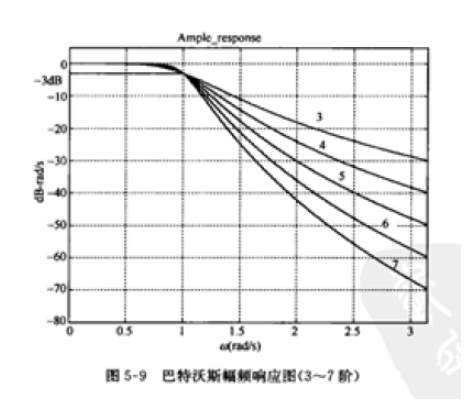
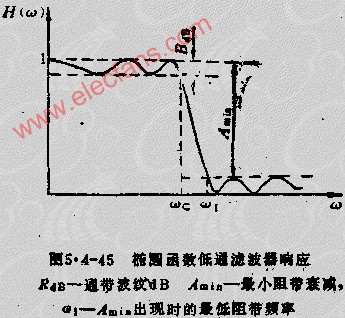
　　D0表示通带的半径，n表示的是巴特沃斯滤波器的次数。随着次数的增加，振铃现象会越来越明显。

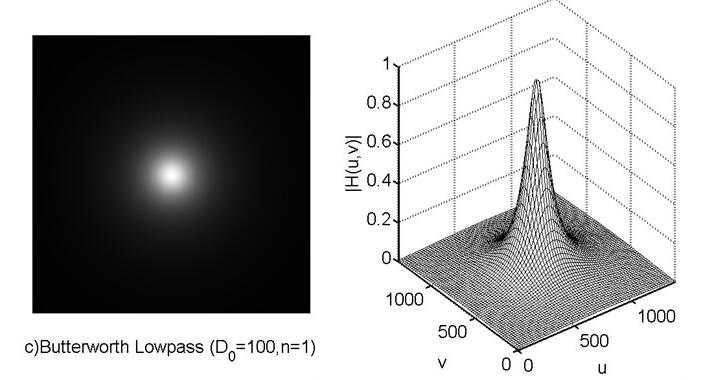
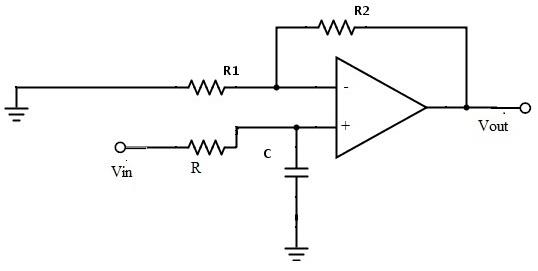
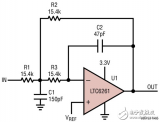
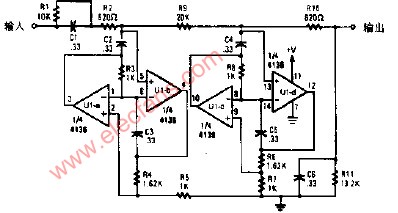
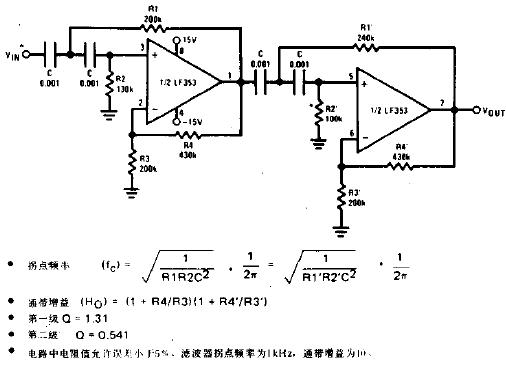
　　巴特沃斯低通滤波器原理图

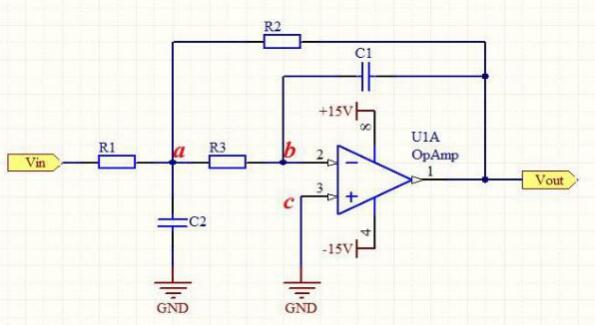
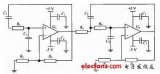
　　图3二阶巴特沃斯低通滤波器原理图

　　基于以上对有源一阶RC 低通滤波器、积分器以及两者之间的区别于联系的分析，在此给出阶巴特沃斯低通滤波器的原理图如下图3 所示：

　　根据巴特沃斯-阶低通滤波器的原理图可知，在该滤波电路中R和C，构成低通级，R3和G构成积分环节，这两级电路同时表现出低通特性。

　　巴特沃斯滤波器优点

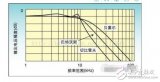
　　巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。在振幅的对数对角频率的波得图上，从某一边界角频率开始，振幅随着角频率的增加而逐渐减少，趋向负无穷大。

　　一阶巴特沃斯滤波器的衰减率为每倍频6分贝，每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝，三阶巴特沃斯滤波器的衰减率为每倍频18分贝，如此类推。巴特沃斯滤波器的振幅对角频率单调下降，并且也是唯一的无论阶数、振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高，在阻频带振幅衰减速度越快。其他滤波器高阶的振幅对角频率图和低级数的振幅对角频率有不同的形状。

　　巴特沃斯滤波器缺点

　　巴特沃斯滤波器是滤波器的一种设计分类，类同于切比雪夫滤波器，它有高通，低通，带通，高通，带阻等多种滤波器。它在通频带内外都有平稳的幅频特性，但有较长的过渡带，在过渡带上很容易造成失真，小编在调用MATLAB里的巴特沃斯滤波器做仿真时，信号总会在第一个周期略微有些失真。但往后的幅频特性就非常的好。

　　推荐阅读：

　　什么是巴特沃斯滤波器_巴特沃斯滤波器主要参数介绍

　　巴特沃斯滤波器的原理_巴特沃斯滤波器优点介绍