谐波分析法 harmonic analysis method
任何复杂的波都可以由许多不同频率、振幅和位相的正弦分量组合成,谐波分析是将其分解。谐波分析可用以确定非线性畸变。一般非正弦波的高次谐波振幅较小,在测量中只要分析测量二次谐波和三次谐波与基波振幅的比较即可,对于更高次谐波可以不考虑
常有的谐波分析工具有哪些?
一般谐波分析最常用的是电能质量分析仪,可分析总谐波畸变率、谐波直流分量、谐波、间谐波、高次谐波、谐波子组。在谐波的测试项目方面都非常全面,而且谐波可以通过柱状图显示各次谐波的含量,也可以通过表格图查看有效值、相位角、含量。基本能满足谐波分析的所有需求。
市面上较为推荐的是致远电子的E6000电能质量分析仪,不仅仅在总端机器谐波分析非常全面。谐波:1~50次、0~49间谐波、1~35高次谐波、1~50次谐波子组、电流K系数。等等。而且配置的分析软件功能非常强大,能够直接产生统计报表及数据报表,给测量的后期工作省了不少功夫。
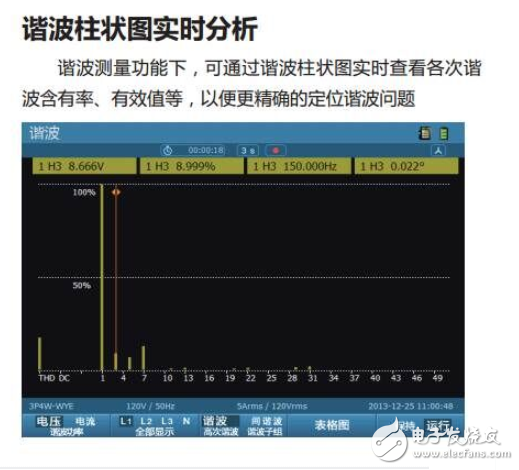
随着用电设备的多样化和复杂化,线路中谐波的成分也变得越来越丰富,谐波污染的治理问题也变得越来越棘手,许多仪器也相应推出了谐波测量功能,我们该如何区分这些谐波的测量方法并正确地使用他们进行谐波测量呢?
谐波分析的分析方法
满足一定条件(Dirichlet条件)的、以T为周期的时间的周期函数f(t),在连续点处,可用下述的三角函数的线性组合(傅里叶级数)来表示:上式称为f(t)的傅里叶级数,其中,ω=2π/T。n为整数,n》=0。n为整数,n》=1。在间断点处,下式成立:a0/2为信号f(t)的直流分量。
令c1为基波幅值,cn为n次谐波的幅值。c1有时也称1次谐波的幅值。a0/2有时也称0次谐波的幅值。非正弦波里含有大量的谐波,不同的波形里含有不同的谐波成份。在倍频器、变频器里,就必须要进行谐波分析,分柝各次谐波的分布;在乐器、音响、放大器……也要分析谐波成份。
(1)奇次谐波,指频率为基波频率的3、5、7……倍的谐波;
(2)偶次谐波,指频率是基波频率的2、4、6……倍的谐波。对f(t)=-f(t+T/2) 的函数(T为函数周期),偶次谐波及直流分量为0;对f(t)=f(t+T/2) 的函数(T为函数周期), 奇次谐波为0。
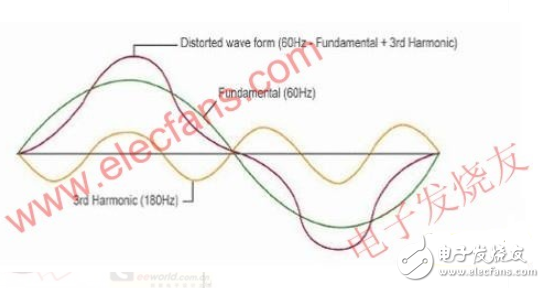
谐波分析方法对比
在很多人认识里,只有使用同步采样才能进行精确的谐波分析,其实采用非同步采样同样能进行谐波分析,而且在许多情况下甚至比同步采样法更优秀。PA功率分析仪提供了常规谐波、谐波和IEC谐波三种谐波测量模式,支持同步和非同步的谐波分析,将两种分析方式互补使用可提高谐波的分析能力。下面通过其计算方法的简单,结合实例讨论三种谐波模式的使用。
谐波测量基本原理
目前最常用的谐波分析方法是使用傅里叶变换,将时域的离散信号进行傅里叶级数展开,得到离散的频谱,从离散的频谱中挑选出各次谐波对应的谱线,计算得出谐波各项参数。
在实际实现时,由于离散傅里叶变换存在“栅栏效应”,采样频率不为基波的整数倍时,部分谐波可能不在离散傅里叶变换后的离散频率点上,需要使用特殊的手段将栅栏空隙对准我们关心的谐波频率点。其中同步采样法和频率重心法使用最为广泛。

同步采样法
顾名思义,就是使采样频率与基波频率同步改变。该方法从源头上保证数据的采样频率为基波频率的整数倍,如IEC 61000-4-7标准就规定50Hz使用10倍基波采样率,采样数据经离散傅里叶变换即可得到各次谐波分量。同步采样常用硬件PLL实现,需要实时调整采样频率,频率的锁定需要时间,受限于滤波器及相关器件,很难做到很宽的频域,也很难保证频谱特别丰富时的准确性。
频率重心法
使用足够高的采样频率(一般大于4倍基波频率)即可满足直接对信号进行采样,将信号的频谱间隔拉开,并且使用更多周期的数据点做离散傅里叶变换,降低频谱泄露的影响。最后根据窗函数的功率谱分布特性,通过频谱的谱峰和次谱峰,找到真正的谱峰频点——即离散频谱的谱峰和次谱峰的重心。通过频率重心法消除了栅栏效应的影响,对各次谐波使用重心法,还得到一个偏离系数,使用该系数配合窗函数功率谱,可求解得到对应频点的相位和幅值等信息。至此,非同步采样法同样得到了各次谐波。受限于窗函数的频谱特性,该法需要用足够高采样率来保证各频率成分的频谱互相影响足够小;而且截断造成的泄漏也不能太大,否则产生的假频率叠加到真实频谱里,导致结果误差更大。
简单对比
基于以上实现原理可知,同步采样法精度取决于PLL的准确度,而后期计算简单。PLL中用到的滤波器限制了支持的基波频率上限,因此在基波频率较高时,同步采样法一般无法支持;同样是滤波器原因,无法很好滤除低偶次谐波,所以低偶次谐波幅值较大时,PLL就无法同步基波采样,谐波分析结果也就完全错误。
频率重心法不需要额外滤波器,采样器件可工作在支持的最高采样频率,使有效谱线拉开的同时提高了支持的谐波频率范围,而为了消除泄漏的影响,需要使用更多的数据进行傅里叶变换。所以频率重心法引入了数倍于同步采样法的计算量。另外,重心法需要使用至少两根谱线,而且受窗函数主瓣宽度限制,频率重心法所能支持的频率下限只能达到频率分辨率的三倍以上。由于频率重心法没有反馈过程,不依赖于信号,模拟电路实现简单,理论上只要采样率和使用的数据点足够,就能得到正确的结果。
特别地,因为同步采样需要硬件电路,受限与成本与体积,大部分测量仪器只支持一到两个PLL源,而频率重心法无此限制,甚至可任意定义基波源(对应于PLL源,用于确定基波)。
应用实例
PA功率分析仪提供了三种谐波模式:常规谐波、谐波和IEC谐波。其中常规谐波对应频率重心法、谐波和IEC谐波对应同步采样法。谐波和IEC谐波区别在于IEC谐波完全按照IEC 61000-4-7标准规定的倍频数FFT点数进行计算,并增加了标准规定的处理流程和计算参数。下面使用实例信号对比两种方法的区别:
信号一:基波频率50Hz,含2~15次谐波,各次含量均为10%
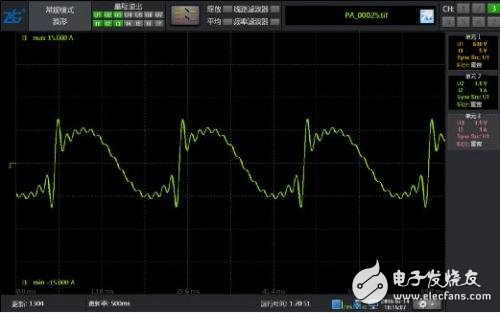
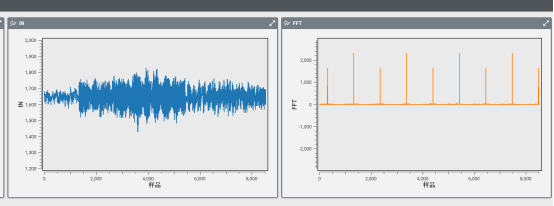
图 1 50Hz基波2~15次含量10% 谐波波形
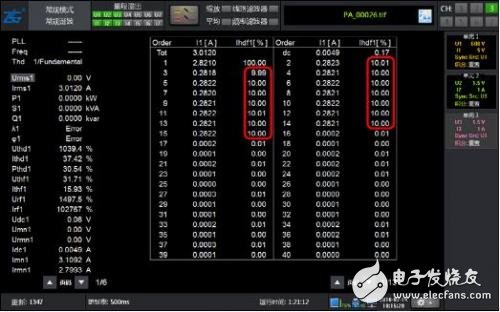
图 2 50Hz基波2~15次含量10% 谐波常规谐波分析结果
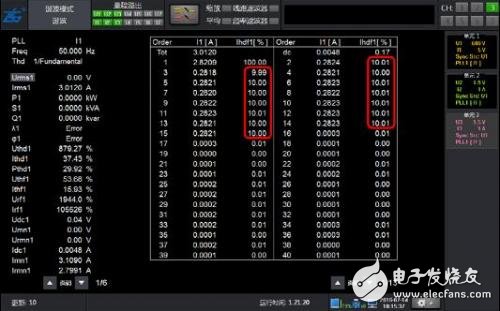
图 3 50Hz基波2~15次含量10% 谐波的谐波模式分析结果
如图 1所示包含谐波的50Hz信号波形,常规谐波和谐波模式谐波均能得到正确的谐波含量,并且精度很高。
信号二:基波频率50Hz,含2~15的奇次谐波,各次含量同样均为10%

图 4 50Hz基波2~15奇次含量10% 谐波波形
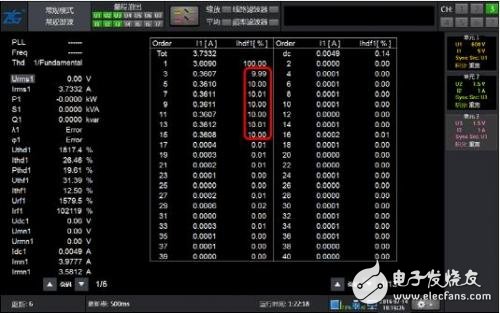
图 5 50Hz基波2~15奇次含量10% 常规谐波分析结果
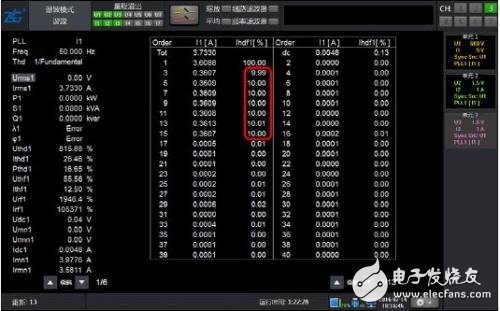
图 6 50Hz基波2~15奇次含量10% 谐波模式分析结果
如图 4所示只包含2~15次的奇次谐波的波形,常规谐波和谐波模式结果同样精确。
信号三:基波频率50,含2~15偶次谐波,各次含量均为10%

图 7 50Hz基波2~15偶次含量10% 谐波波形
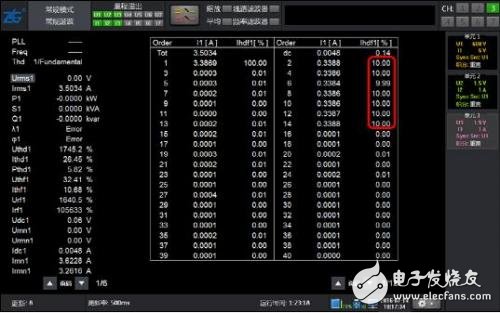
图 8 50Hz基波2~15偶次含量10% 常规谐波分析结果
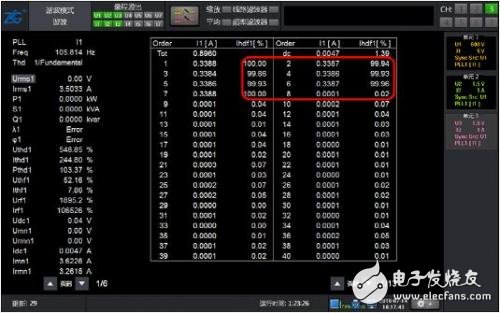
图 9 50Hz基波2~15偶次含量10% 谐波模式分析结果
如图 7所示只包含50Hz基波的2~15次的偶次谐波的波形,受偶次谐波的影响,每个基波周期多了两次过零,而且频率与基波相近,PLL的滤波器亦无法滤除该谐波,因此PLL结果错误,导致谐波分析结果也完全错误,此时的常规谐波分析结果仍然正确,而且保持了很高的精度。说明常规谐波可以不受偶次谐波影响,在采样率和FFT点数足够时,具有受被测信号影响低的优势。
信号四:基波频率6kHz,含2~15次谐波,各次含量均为10%
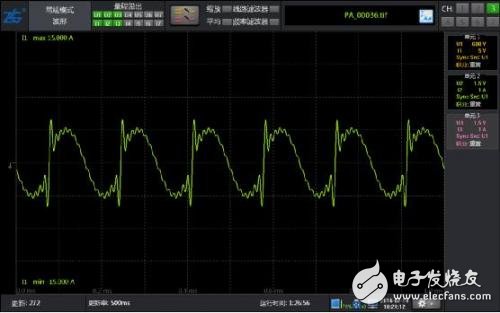
图 10 6kHz基波2~15次含量10% 谐波波形
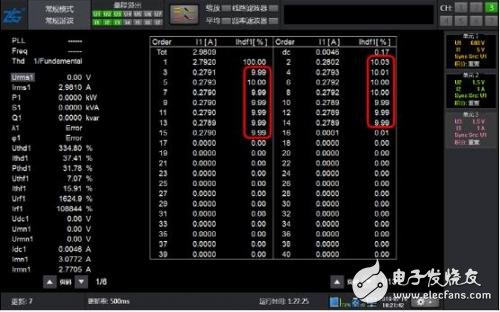
图 11 6kHz基波2~15次含量10% 常规谐波分析结果
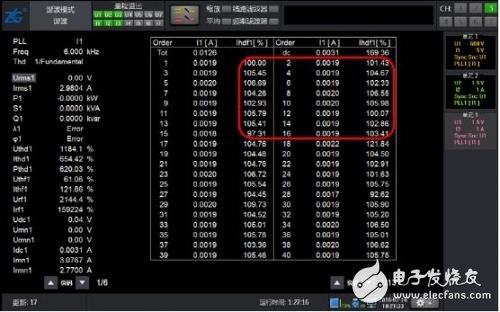
图 12 6kHz基波2~15次含量10% 谐波模式分析结果
如图 10 所示包含6kHz基波的2~15次谐波的波形,由于已经超出谐波模式支持的频率范围,谐波模式无法测量,而常规谐波分析时使用了200kHz的采样率,6kHz的15次谐波频率为90kHz,小于采样频率的一半,因此仍然可以精确测量。
总结
由上实例看出,非同步采样拓宽了谐波的分析范围,在许多同步采样受到约束的场合可以实现互补,是一种强有力的谐波分析方法。
需要指出的是,虽然以上用例中常规谐波分析结果都正确且精度很高,但在谐波模式PLL正确时,谐波模式在高次谐波的稳定性和精度会比常规谐波高,因为常规谐波在高次谐波的频率上有累积误差,且频谱两端会受负频率的影响。特别需要注意常规谐波一个致命缺点是频率下限较高(PA5000功率分析仪的常规谐波支持基波的频率下限是15Hz),而且需要保证更新周期内有足够的采用点。
 电子发烧友App
电子发烧友App



















评论