波特图的定义
波特图是线性非时变系统的传递函数对频率的半对数坐标图,其横轴是频率,纵轴以对数尺度(logscale)表示,利用波特图可以看出系统的频率响应。波特图一般是由二张图组合而成,一张幅频图表示频率响应增益的分贝值对频率的变化,另一张相频图则是频率响应的相位对频率的变化。
波特图可以用电脑软件(如MATLAB)或仪器绘制,也可以自行绘制。利用波特图可以看出在不同频率下,系统增益的大小及相位,也可以看出大小及相位随频率变化的趋势。
波特图的图形和系统的增益,极点、零点的个数及位置有关,只要知道相关的资料,配合简单的计算就可以画出近似的波特图,这是使用波特图的好处。
波特图(Bode Plots)
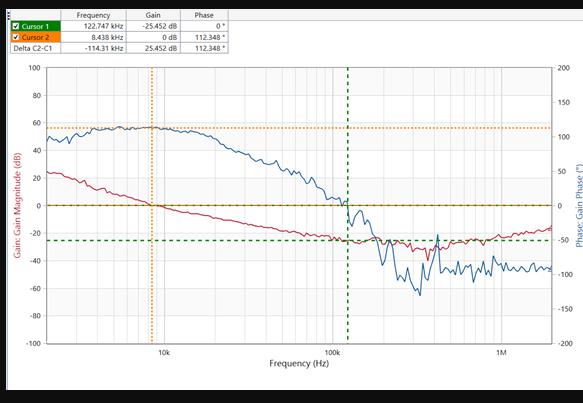
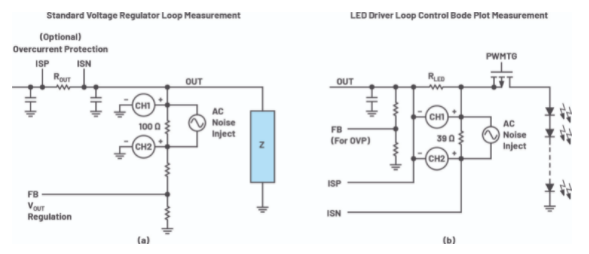
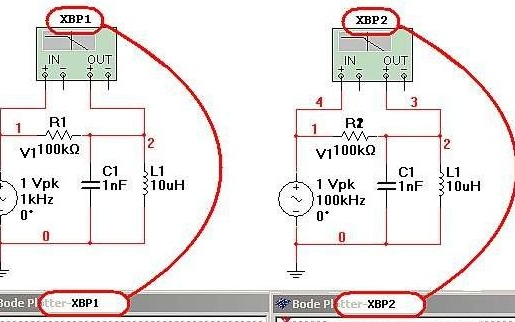
波特图(Bode Plots)可用来确认回路的稳定性,回路的增益(Loop Gain,单位:dB)是频率(Frequency)的函数(图5:典型的波特图)。 回路增益可以用网络分析仪(Network Analyzer)测量。 网络分析仪向反馈回路(Feedback Path)注入低电平的正弦波(Sine Wave),随着直流电压(DC)的不断升高, 这些正弦波信号完成扫频,直到增益下降到0dB。然后测量增益的响应(Gain Response)。
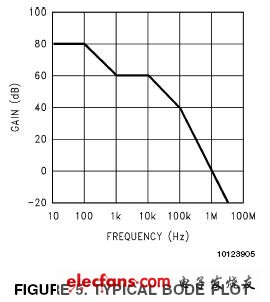
图5
波特图是很方便的工具,它包含判断闭环系统(Closed-loop System)稳定性的所有必要信息。 包括下面几个关键参数:环路增益(Loop Gain),相位裕度(Phase Margin)和零点(Zeros)、极点(Poles)。
波特图分析
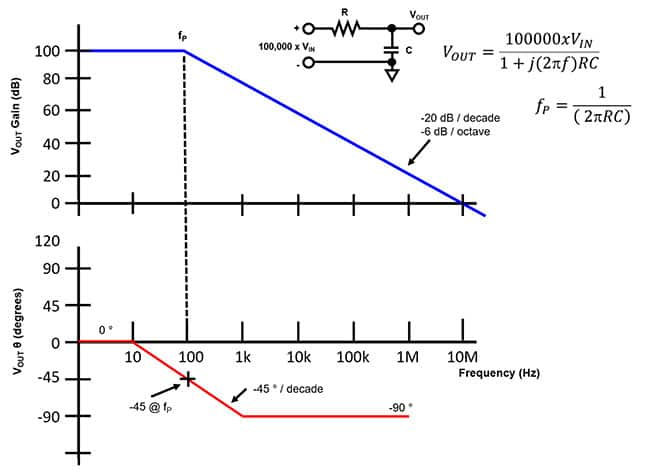
用包含三个极点和一个零点的波特图(图11:波特图)来分析增益和相位裕度。
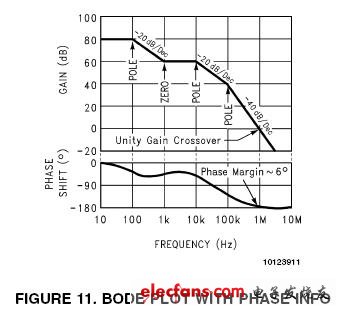
图11
假设直流增益(DC gain)为80dB,第一个极点(pole)发生在100Hz处。在此频率,增益曲线的斜度变为-20dB/十倍频程。1kHz处的零点使斜度变为0dB/十倍频程,到10kHz处斜度又变成-20dB/十倍频程。在100kHz处的第三个也是最后一个极点将斜度最终变为-40dB/十倍频程。
图11中可看到单位增益点(Unity Gain Crossover,0dB)的交点频率(Crossover Frequency)是1MHz。0dB频率有时也称为回路带宽(Loop Bandwidth)。
相位偏移图表示了零、极点的不同分布对反馈信号的影响。为了产生这个图,就要根据分布的零点、极点计算相移的总和。在任意频率(f)上的极点相移,可以通过下式计算获得: 极点相移 = -arctan(f/fp) (6)
在任意频率(f)上的零点相移,可以通过下式计算获得: 零点相移 = -arctan(f/fz) (7)
此回路稳定吗?为了回答这个问题,我们根本无需复杂的计算,只需要知道0dB时的相移(此例中是1MHz)。
前两个极点和第一个零点分布使相位从-180°变到+90°,最终导致网络相位转变到-90°。最后一个极点在十倍频程中出现了0dB点。代入零点相移公式,可以计算出该极点产生了-84°的相移(在1MHz时)。加上原来的-90°相移,全部的相移是-174°(也就是说相位裕度是6°)。由此得出结论,该回路不能保持稳定,可能会引起振荡。
 电子发烧友App
电子发烧友App










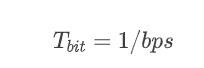
















评论