电子发烧友App
本文主要是关于分组码和卷积码的相关介绍，并着重阐述了分组码和卷积码不同特性。
卷积码
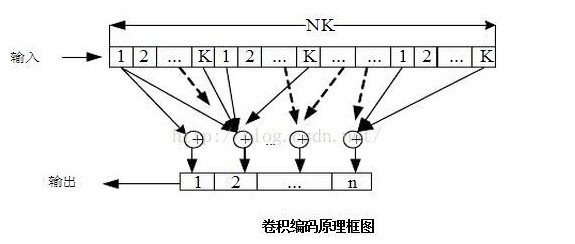
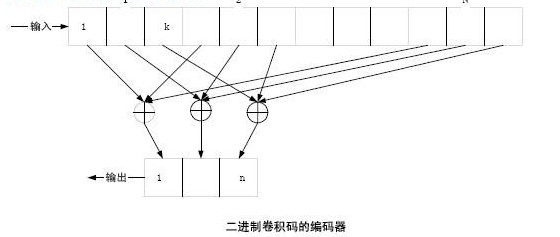
卷积码是1955年由Elias等人提出的，是一种非常有前途的编码方法。我们在一些资料上可以找到关于分组码的一些介绍，分组码的实现是将编码信息分组单独进行编码，因此无论是在编码还是译码的过程中不同码组之间的码元无关。卷积码和分组码的根本区别在于，它不是把信息序列分组后再进行单独编码，而是由连续输入的信息序列得到连续输出的已编码序列。
即进行分组编码时，其本组中的n-k个校验元仅与本组的k个信息元有关，而与其它各组信息无关；但在卷积码中，其编码器将k个信息码元编为n个码元时，这n个码元不仅与当前段的k个信息有关，而且与前面的（m－1）段信息有关（m为编码的约束长度）。
同样，在卷积码译码过程中，不仅从此时刻收到的码组中提取译码信息，而且还要利用以前或以后各时刻收到的码组中提取有关信息。而且卷积码的纠错能力随约束长度的增加而增强，差错率则随着约束长度增加而呈指数下降 。卷积码（n，k，m） 主要用来纠随机错误，它的码元与前后码元有一定的约束关系，编码复杂度可用编码约束长度m*n来表示。一般地，最小距离d表明了卷积码在连续m段以内的距离特性，该码可以在m个连续码流内纠正（d-1）/2个错误。卷积码的纠错能力不仅与约束长度有关，还与采用的译码方式有关。总之，由于n，k较小，且利用了各组之间的相关性，在同样的码率和设备的复杂性条件下，无论理论上还是实践上都证明：卷积码的性能至少不比分组码差。
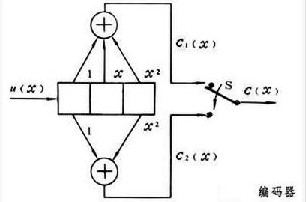
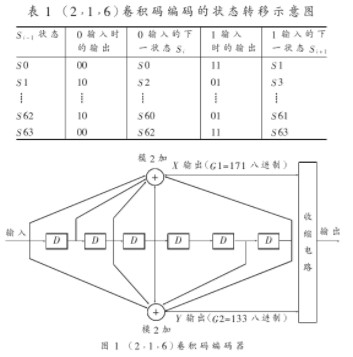
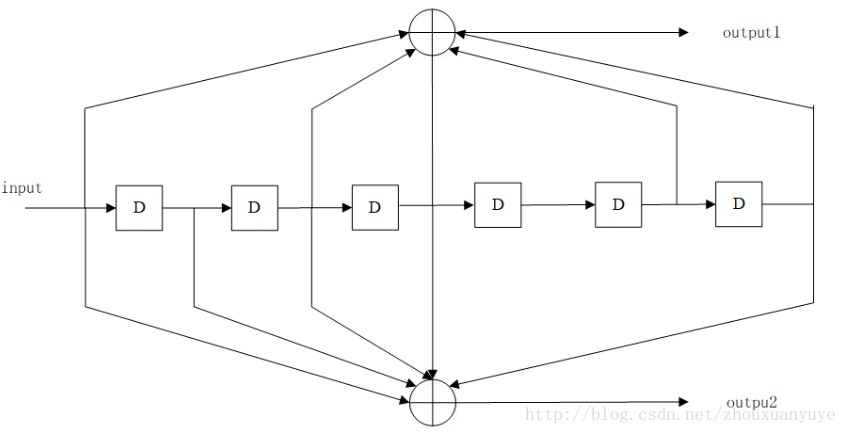
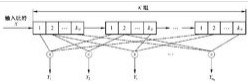
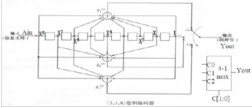
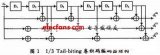
以二元码为例，编码器如图。输入信息序列为u＝(u0，u1，…)，其多项式表示为u(x)＝u0+u1x＋…＋ulxl＋…。编码器的连接可用多项式表示为g(1,1)(x)＝1+x+x2和g(1,2)(x)＝1+x2，称为码的子生成多项式。它们的系数矢量g(1,1)=(111)和g(1,2)=(101)称作码的子生成元。以子生成多项式为阵元构成的多项式矩阵G(x)＝[g(1,1)(x),g(1,2)(x)]，称为码的生成多项式矩阵。由生成元构成的半无限矩阵
称为码的生成矩阵。其中(11,10,11)是由g(1,1)和g(1,2)交叉连接构成。编码器输出序列为c＝u·G，称为码序列，其多项式表示为c(x)，它可看作是两个子码序列c(1)(x)和c(2)(x)经过合路开关S合成的，其中c(1)(x)＝u(x)g(1,1)(x)和c(2)(x)＝u(x)g(1,2)(x),它们分别是信息序列和相应子生成元的卷积，卷积码由此得名。
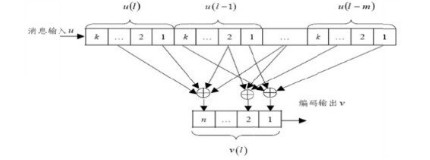
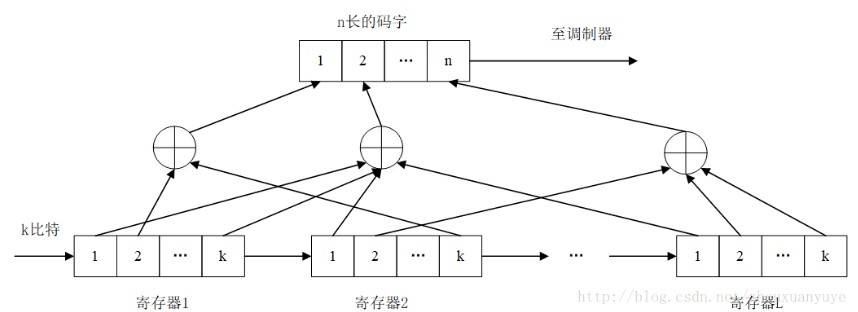
在一般情况下，输入信息序列经过一个时分开关被分成k0个子序列,分别以u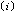
(x)表示,其中i=1，2,…k0，即u(x)＝[u
(x),…,u
(x)]。编码器的结构由k0×n0阶生成多项式矩阵给定。输出码序列由n0个子序列组成，即c(x)＝[c(x),c
(x)，…，c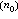
(x)]，且c(x)=u(x)·G(x)。若m是所有子生成多项式g
(x)中最高次式的次数，称这种码为(n0，k0，m)卷积码。
分组码
一类重要的纠错码，它把信源待发的信息序列按固定的κ位一组划分成消息组,再将每一消息组独立变换成长为n(n＞κ)的二进制数字组,称为码字。如果消息组的数目为M(显然M≤2κ),由此所获得的M个码字的全体便称为码长为n、信息数目为M的分组码,记为【n，M】。把消息组变换成码字的过程称为编码，其逆过程称为译码。
线性分组码与非线性分组码 分组码就其构成方式可分为线性分组码与非线性分组码。
线性分组码是指【n,M】分组码中的M个码字之间具有一定的线性约束关系,即这些码字总体构成了n维线性空间的一个κ维子空间。称此κ维子空间为(n，κ)线性分组码，n为码长，κ为信息位。此处M＝2κ。
非线性分组码【n，M】是指M个码字之间不存在线性约束关系的分组码。d为M个码字之间的最小距离。非线性分组码常记为【n，M，d】。非线性分组码的优点是：对于给定的最小距离d,可以获得最大可能的码字数目。非线性分组码的编码和译码因码类不同而异。虽然预料非线性分组码会比线性分组码具有更好的特性，但在理论上和实用上尚缺乏深入研究（见非线性码）。
线性分组码的编码和译码 用Vn表示 GF(2)域的n维线性空间，Vκ是Vn的κ维子空间，表示一个(n，κ)线性分组码。Ei=（vi1，vi2…,vin）是代表Vκ的一组基底(i=1，2，…，κ)。以这组基底构成的矩阵
称为该(n,κ)线性码的生成矩阵。对于给定的消息组m＝(m1，m2，…，mκ)，按生成矩阵G，m被编为
mG＝m1E1＋m2E2＋…＋mκEκ
这就是线性分组码的编码规则。若
之秩为n-κ并且满足GHT=0，仅当
=(v1,v2,…，vn)∈n满足HT =0时，才为κ中的码字。称H为(n，κ)线性分组码κ的均等校验矩阵,称HT为矢量的伴随式。假设 v是发送的码矢量，在接收端获得一个失真的矢量r＝v＋E,式中E＝(e1，e2，…，en)称为错误型。由此
rHT＝(v＋e)HT＝eHT
线性码的译码原则便以此为基础。
汉明码 这是最早提出的一类线性分组码，已广泛应用于计算机和通信设备。它是由R.W.汉明于1950年提出的。若码的均等校验矩阵H由2r-1个、按任一次序排列且彼此相异的二进制 r维列矢量构成。这样得到的线性分组码称为汉明码，其分组长为n=2r-1，信息位为κ=n-r =2r-1-r，即为(2r-1，2r-1-r)码。例如，以矩阵
为均等校验矩阵的线性分组码便为(7，4)汉明码。汉明码的译码十分简单。例如, 假定=(1001100)为发送的码字,其第3位有错，即接收矢量为r =(1011100)。于是
恰为矩阵H的第 3 列，因而判定原来发送的码字为=(1001100)。这种译码方式是一般性的。如果接收矢量r在第i位有错,则其伴随式HrT刚好为矩阵H的第i列。汉明码是可以纠正单个错误的线性分组码。
循环码 具有某种循环特性的线性分组码，如果(n，κ)线性分组码Vκ具有如下的性质:对于每一个=(ɑ0,ɑ1，…，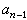
)∈Vn，只要∈Vκ,其循环移位(
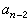)亦属于Vκ,则称Vκ为循环码。循环码的优点在于其编码和译码手续比一般线性码简单，因而易于在设备上实现。使Vn中的每一个矢量=(ɑ0，ɑ1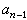，…，),对应于域GF(2)上的多项式ɑ(x)=ɑ0+ɑ1x +…+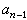xn-1。于是Vn中的全体n维矢量便与上述多项式之间建立了一一对应的关系。基于这种对应,使Vn中除了线性运算而外，还建立了矢量之间的乘法运算。A=(ɑ0,ɑ1,…,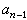)与B=(b0,b1,…,
)的乘积ab可视为ɑ(x)b(x)【mod(xn-1)】所对应的矢量。因此,一个(n,κ)循环码的生成矩阵及均等校验矩阵可分别由生成多项式及均等校验多项式h(x)所代替，从而简化了编码及译码运算。
BCH码 它是一类重要的循环码，能纠正多个错误。假设m是满足2m呏1(mod n)的最小正整数,β是域GF(2m)的n次单位原根,作循环码的生成多项式g(x),以d0-1个接续的元素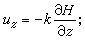
为根，其中m0,d0均为正整数，且d0≥2。于是
其中mj(x)代表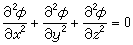
的最小多项式。由这个g(x)所生成的，分组长为 n的循环码称为BCH码。它由R.C.Bose，D.K.Ray-Chaudhuri及A.Hocquenghem三人研究而得名。BCH码的主要数量指标是：码长n，首元指数m0，设计距离d0，信息位数
（
表示多项式 g(x)的次数）。BCH码的重要特性在于：设计距离为d0的BCH码，其最小距离至少为d0，从而可至少纠正
个独立错误。BCH码译码的第一步是计算伴随式。假设 
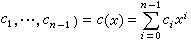为发送码矢量,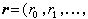
为接收矢量,而E＝(E0,E1,…,En-1)为错误矢量,或记为
称为错误多项式。于是伴随矢量之诸S=(S1，S2，…,S2t)分量Sκ由
决定（κ=1,2,…2t；为简便计,设m0=1,d0=2t+1）。假设有e个错误出现(1≤e≤t),则对应于e个错误的Ei厵0。如果E 的第j个（从左至右）非零分量是Ei,则称Xj=βi为这个错误Ei的错位，而称Yj＝Ei为这个错误的错值。称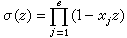
为错位多项式。BCH码译码的关键是由诸sκ(κ=1,2，…，2t)求出
(z)。这可用著名的伯利坎普－梅西迭代算法来完成。这种算法相当于线性移位寄存器的综合问题。最后一步是求出(z)的全部根，可用钱天闻搜索算法完成,从而可以定出接收矢量r的全部错位。
里德-索洛蒙码 这是一种特殊的非二进制BCH码。对于任意选取的正整数s,可构造一个相应的码长为n=qs-1的q进制BCH码,其中码元符号取自有限域GF(q)，其中q为某一素数的幂。当s=1,q＞2时所建立的码长为n=q-1的q进制BCH码便称为里德-索洛蒙码,简称为RS码。当q=2m(m＞1),码元符号取自域GF(2m)的二进制RS码可用来纠正成区间出现的突发错误。这种码在短波信道中特别有用。
戈帕码 这是一种重要的线性分组码，它不仅包括常见的诸如本原BCH码等大量的循环码类,还包括相当多的非循环线性分组码类，并且后一种码具有良好的渐近特性。戈帕码的理论实质在于将每一个码矢量与一个有理分式相对应。q是某一个素数幂，g(z)是域GF(qm)上的任意多项式，L表示域GF(qm)中所有不为g(z)之根的元素所成之集合，|L|代表L中元素的数目。于是存在一个以GF(q)为符号域，以GF(qm)为位置域的线性分组码。码长为|L|，它的各码元用L中的元素来标志。这种码可定义为满足条件
的一切GF(q)上的全体|L|维矢量
的集合，式中
这种码称为戈帕码，称g(z)为戈帕多项式。
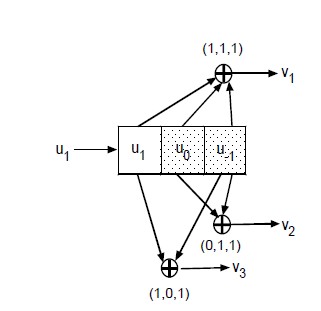
例如，q＝2,m＝2，g(z)＝z+α,α 是域GF(z2)上的本原元素
α2＋α＋1＝0 α3＝1
则
L＝｛β1,β2,β3｝＝｛0,1,α2｝
于是
可验证,(1，1，1)即为这一戈帕码的码字。戈帕码也有类似于BCH码的译码方法。
自50年代分组码的理论获得发展以来，分组码在数字通信系统和数据存储系统中已被广泛应用。由于大规模和超大规模集成电路的迅速发展，人们开始从易于实现的循环码理论研究中解脱出来，更重视研究性能良好的非循环线性分组码和非线性分组码。人们在分组码研究中又引进了频谱方法，这一研究方向受到了较多的注意。
结语
关于分组码和卷积码的区别就介绍到这了，希望通过本文能让你对分组码和卷积码有更深的了解。
工商网监
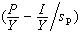
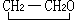
评论