数字图像处理的基本步骤:
(处理图像)图像获取--》图像滤波与增强--》图像复原--》彩色图像处理--》小波与多分辨率处理--》压缩--》形态学处理--》( 图像属性)分割--》表示和描述--》目标识别
图像的感知和获取:
1)、单个传感器获取;
2)、条带传感器获取;
3)、传感器阵列获取;
图像形成模型:
一副平面图像可以用二维亮度函数来表示,当一副图像从物理过程产生时,它的值正比于物理源的辐射能量,因此,f(x,y)一定是非零和有限的,即:
;
当用数学方法描述图像信息时,通常着重考虑它的点的性质。例如一副图像可以被看作是空间各个坐标点的结合。它的最普通的数学表达式为:其中(x,y,z)是空间坐标,λ是波长,t是时间,I是图像强度。这样一个表达式可以代表一副活动的、彩色的、立体图像。当研究的是静止图像时,则与时间t无关,当是单色图像时,与波长λ无关,对于平面图像则与坐标z无关。因此,对于静止的平面的、单色的图像来说其数学表达式可简化为:
人们所感受到的图像一般都是由物体反射的光组成的。函数f(x,y)可由两个分量来表示:入射到观察场景的光源总量;场景中物体反射光的总量。这两个分量分别称为入射分量和反射分量,如果用i(x,y)表示入射分量,用r(x,y)表示反射分量,两个函数合并形成f(x,y),即:
; 其中:,
图像的取样和量化
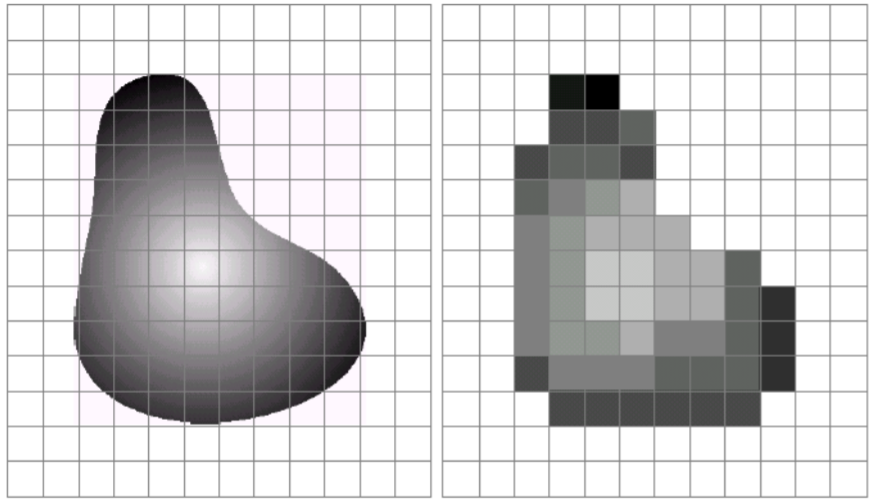
图像取样
◆ 在取样时,若横向的像素数(列数)为M ,纵向的像素数(行数)为N,则图像总像素数为M*N个像素。
◆ 一般来说,采样间隔越大,所得图像像素数越少,空间分辨率低,质量差,严重时出现马赛克效应;采样间隔越小,所得图像像素数越多,空间分辨率高,图像质量好,但数据量大。
图像的量化
◆ 量化等级越多,所得图像层次越丰富,灰度分辨率高,图像质量好,但数据量大;量化等级越少,图像层次欠丰富,灰度分辨率低,会出现假轮廓现象,图像质量变差,但数据量小。
模拟图像经过采样后,在时间和空间上离散化为像素。但采样所得的像素值(即灰度值)仍是连续量。把采样后所得的各像素的灰度值从模拟量到离散量的转换称为图像灰度的量化(也就是对现实空间场景的灰度数据进行离散化的操作)。
数字图像表示:
黑白图像
指图像的每个像素只能是黑或者白,没有中间的过渡,故又称为2值图像。2值图像的像素值为0、1。
灰度图像
灰度图像是指每个像素的信息由一个量化的灰度级来描述的图像,没有彩色信息。
彩色图像
彩色图像是指每个像素的信息由RGB三原色构成的图像,其中RBG是由不同的灰度级来描述的。
图像的数字表示
令f(s, t)表示一幅具有两个连续变量s和t的连续图像函数。通过取样和量化, 我们可把该函数转换为数字图像。将该连续图像取样为一个二维阵列f(x,y), 该阵列有M行和N列,其中(x,y)是离散坐标。
在某些讨论中,使用传统的矩阵表示法来表示数字图像及其像素更为方便:
二维矩阵是表示数字图像的重要数学形式。一幅M×N的图像可以表示为矩阵:矩阵中的每个元素称为图像的“像素”。每个像素都有它自己的“位置”和“值”,“值”是这一“位置”像素的颜色或者强度。
假定图像尺寸为M、N,每个像素所具有的离散灰度级数为G;这些量分别取为2的整数幂m,n,k,即M=2m, N=2n,G=2k 则存储这幅图像所需的位数是:;如果图像是正方形,即M=N,当一副图像有灰度级时,实际上通常称该图像为k比特图像。如,一幅图像有256可能的灰度级称为8比特图像。
空间分辨率N :图像中可辨别的最小细节的度量
表示方法:每单位距离(mm)线对(黑白线)数目
每单位距离(mm)点(像素点)数
在美国,用每英寸点数(dpi)表示
key:空间分辨率的度量必须针对空间单位来规定才有意义,单纯的图像大小本身没有意义。
灰度分辨率 k:在灰度级中可分辨的最小变化
即灰度级,指的是用于量化灰度的比特数,通常用2的整数次幂来表示,最常用8bit,bit数的减小倾向于对比度增加
即 2^8 灰度范围[0~255]
Nk平面中等偏爱曲线解读
key:对于有大量细节的图像,可能只需要很少的灰度级
图像内插:
内插是图像放大、收缩、旋转等任务中广泛采用的基本工具(图像重采样)。如由已知像素灰度估计未知位置的像素灰度。
最近邻内插法
直接取原图像中与其距离最近的像素的灰度值为该点的灰度值。
缺点:会产生不希望的人为缺陷,如某些直线边缘的严重失真
设i+u, j+v(i, j为正整数, u, v为大于零小于1的小数,下同)为待求象素坐标,则待求象素灰度的值 f(i+u, j+v) 如下图所示:
如果(i+u, j+v)落在A区,即u《0.5, v《0.5,则将左上角象素的灰度值赋给待求象素,同理,落在D区则赋予右下角象素的灰度值。最邻近元法计算量较小,但可能会造成插值生成的图像灰度上的不连续,在灰度变化的地方可能出现明显的锯齿状。
双线性内插法
用四个最近邻去估计给定位置的灰度值。
图一:
如下图所示:
对于 (i, j+v),f(i, j) 到 f(i, j+1) 的灰度变化为线性关系,则有:
f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)
同理对于 (i+1, j+v) 则有:
f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)
从f(i, j+v) 到 f(i+1, j+v) 的灰度变化也为线性关系,由此可推导出待求象素灰度的计算式如下:
f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)
双线性内插法的计算比最邻近点法复杂,计算量较大,但没有灰度不连续的缺点,结果基本令人满意。它具有低通滤波性质,使高频分量受损,图像轮廓可能会有一点模糊。
双三次内插:
用16个最近邻去估计给定位置的灰度,i.e,对(x,y)处赋灰度值 v(x,y),
16个系数可由(x,y)点的16个最近邻确定,当求和上限改为1时,退化为双线性内插。 双三次内插在保持细节方面比双线性更好,但计算量也更大,双三次内插目前是商业图像编辑软件的标准内插方法。
其他内插方法
采用更多邻点:样条法
采用更复杂技术:小波
像素间的关系
相邻像素
◆ 位于坐标(x, y)的像素p有四个水平和垂直的相邻像素,每个像素距(x, y)一个单位距离。坐标分别为: (x-1, y) , (x+1, y), (x, y-1), (x, y+1)。此像素集合定义为像素p的4邻域, 用 N4(p)表示。
◆ 另外,p有4个对角相邻像素,坐标为:(x-1, y-1) , (x+1, y-1), (x-1, y+1), (x+1, y+1)用ND(p)表示,和N4(P)一起称为P的8邻域,用N8(P)表示。
Neighbors(相邻点):主要有两种定义:4-neighbors 和8-neighbors。4-neighbors 定义较严:一个点周边有四个相邻点(蓝色);8-neighbors 定义较松:一个点周边有八个相邻点(蓝色)。4-neighbors 一定是8-neighbors,反之不一定。
Path(路径):也有4-path 和8-path。4-path 定义较严:一个路径上所有点互为4-neighbors;8-path 定义较松:一个路径上所有点互为8-neighbors。在4-path 定义下,蓝色点不再属于4-neighbor,路径因此断裂。原本在8-path 定义下为连续的路径,在4-path 定义下可能会断裂。
邻接性、连通性、区域和边界
邻接性有两个要素:一个是灰度值的邻接性(值域V)、一个是物理位置的邻接性(邻域,如N4(P)等)。例如,二值图象中,像素值都为1(或都为0)的像素才有可能被称为是邻接的。在一般图像中,可定义一个值域V,V是0到255中的任一个子集。一般我们考虑三种邻接性:
◆ 4邻接:如果点q在N4(P)中,数值在V中,则q和p是4邻接的;
◆ 8邻接:如果点q在N8(P)中,数值在V中,则q和p是8邻接的;
◆ m邻接(混合邻接):满足下列条件的任一个,则具有V中数值的p和q是m连接的。(为了消除8邻接产生的二义性)
(i)q在N4(P)中
(ii)q在ND(P)中,且集合N4(P)∩N4(Q)中没有V值的像素。
连通:对于图像中的某一个像素子集U和其中的两个点p和q,如果p和q之间有一个有U中全部元素构成的通路,那就说p和q是连通的。
连通集:接上,对于U中的元素p,U中能连通到p的元素的集合叫做U的连通分量,如果U只有一个连通分量,那么U就是一个连通集。
区域:令T是图像中的某一个子集,如果T是一个连通集,那么称T是一个区域
距离度量:
1)像素之间距离的定义—对于像素p、q和z,分别具有坐标(x,y),(s,t)和(u,v),如果
(1) D(p,q) ≥ 0 (D(p,q)=0,当且仅当p =q),
(2) D(p,q) = D(q,p)
(3) D(p,z) ≤ D(p,q) + D(q,z)
则称D是距离函数或度量
2)欧式距离定义:
对于这个距离计算法,具有与(x,y)距离小于等于某个值r的像素是:包含在以(x,y)为圆心,以r为半径的圆平面
3)D4距离(城市距离): D4(p,q) = |x – s| + |y – t|
D4距离举例:
具有与(x,y)距离小于等于某个值r的那些像素形成一个菱形,
例如,与点(x,y)(中心点)D4距离小于等于2的像素,形成右边固定距离的轮廓 ,具有D4 = 1的像素是(x,y)的4邻域
4)D8距离(棋盘距离) :D8(p,q) = max(|x – s| ,|y – t|)
D8距离举例
具有与(x,y)距离小于等于某个值r的那些像素形成一个正方形,例如,与点(x,y)(中心点)D8距离小于等于2的像素,形成右边固定距离的轮廓,具有D8 = 1的像素是(x,y)的8邻域。
数学工具:
1、阵列与矩阵操作:
在对一幅图像或多幅图像进行操作时,要首先明白是阵列操作还是矩阵操作。Eg:2x2图像:
阵列计算:
矩阵计算:
2、线性操作和非线性操作:
算子H:对于给定的输入图像f(x, y),产生一幅输出图像g(x, y),即H[f(x, y)] = g(x, y)。
如求和算子:∑[aifi(x, y)] = g(x, y)。
线性算子:
如果满足
H[aifi(x, y) + ajfj(x, y)] = aiH[fi(x, y)] + ajH[fj(x, y)] = aigi(x, y) + ajgj(x, y)
则称H是一个线性算子。最大值操作不是线性算子。
3、算术操作:
图像的算术操作是阵列操作,即在相对应的像素对之间执行。
4种算术操作表示为:
s(x, y) = f(x, y) + g(x, y);
d(x, y) = f(x, y) - g(x, y);
p(x, y) = f(x, y) × g(x, y);
v(x, y) = f(x, y) ÷ g(x, y);
处理图像:
1.利用带噪图像的相加(平均)进行降噪处理。
2.利用图像相减增强差别。
3.利用图像相乘和相除来校正阴影。
给定一幅图像f,保证图像间的算术操作的整个值域落入到某个固定比特数的方法,执行以下两步:
fm = f-min(f)
fs = K[fm/max(fm)]
注意:在执行除法操作时,需要将一个较小的数加到除数图像的像素上,以避免用0去除。
4、集合和逻辑操作:
1)、基本集合操作:属于,包含,交差并补等。
灰度图像的集合操作:灰度值的并集操作和交集操作通常分别定义为相应像素对的最大和最小,而补集操作定义为常数与图像中每个像素的灰度间的两两之差。
如:灰度级图像的元素用集合A表示,其中元素是三元组形式(x,y,z),x与y为空间坐标,z为灰度。补集:
Ac={(x, y, K-z)|(x, y, z)∈A};
其中K = 2k - 1,k为表示z的灰度的比特数。
如
An = Ac={(x, y, 255-z)|(x, y, z)∈A};
同理,两个灰度集合A和B的并集可定义为集合
A∪B = {max(a, b)|a∈A, b∈B};
2)、基本的逻辑操作:AND, OR, NOT, XOR
3)、模糊集合
令U代表所有的人,令A为U的子集,为年轻人的集合。引入隶属度函数对U中每个元素赋值。隶属度函数简单地定义为一个阈值,低于该阈值的为年轻人,高于该阈值的为非年轻人。思考:假设20岁为阈值,20岁为年轻人,20岁零一秒就不是年轻人了?所以需要更多的灵活性,即从年轻到非年轻过渡。使用模糊集合可以声明一个人的年轻度为50%。换句话说,年龄是一个不精确的概念,而模糊逻辑提供处理这种概念的工具。
5、空间操作
空间操作直接在给定图像的像素上执行,分为三类:单像素操作、邻域操作、几何空间变换
一、单像素操作
s = T(z),
其中,z是原图像中像素的灰度,s是处理后图像中相应像素的(映射)灰度,T为变换函数。
二、邻域操作
与单像素操作类似,Sxy代表图像f中任意一点(x, y)为中心的邻域集,邻域处理是在Sxy内的像素经指定操作后输出到另一图像相同坐标处,形成新图像g。
三、几何空间变换
几何空间变换主要由两个基本操作组成:(1)、坐标的空间变换;(2)、灰度内插;
最常用的空间坐标变换之一是仿射变换。
其中(v, w)是原图像中像素的坐标,(x, y)是变换后图像中像素的坐标。
基于上式,可以实现恒等变换、尺度变换、旋转变换、平移变换、垂直偏移变换、水平偏移变换。
如垂直偏移变换:
图像配准:
用于对齐两幅或多幅相同场景的图片。
图像配准需要输入图像与参考图像。输入图像是我们希望变换的图像,参考图像是想要配准输入图像的图像。
图像配准的主要方法是使用约束点,输入图像产生输出图形的特定变换通常是不知道,所以需要估计变换函数,而估计变换函数问题是建模问题之一。
基于双线性近似的简单模型:
x = c1v + c2w + c3vw + c4;
y = c5v + c6w + c7vw + c8;
(v, w)和(x, y)分别是输入图像和参考图像中约束点的坐标。如果在两幅图像中有四对相应的约束点,则可以解出8个未知参数。这样构成简单模型,从而可以把一幅图像的像素变换为另一幅图像的像素位置。也可以选择更复杂的模型,如最小均方算法等。
6、向量和矩阵操作
多光谱图像处理是使用向量和矩阵操作的典型领域。
如:RGB图像的每个像素都有三个分量(z1:红色图像中的亮度;z2:绿色图像中的亮度;z3:蓝色图像中的亮度)形成三维向量
多光谱需要n幅分量图像,形成n维向量【可以使用向量矩阵理论工具】
7、图像变换:
之前的图像处理方法都是直接在图像像素上进行操作,但是某些情况下,通过变换输入图像来表达图像处理任务,在变化域执行指定任务,之后再用反变换返回到空间域会更好。
变换对 :T(u,v) ---正变换核; R[T(u,v)]----反变换核;
8、概率方法:有很多应用,此处不一一列举。
 电子发烧友App
电子发烧友App

























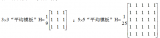
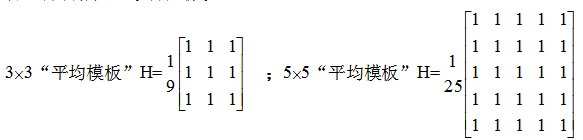










评论