蝶形运算,2点DFT运算称为蝶形运算,而整个FFT就是由若干级迭代的蝶形运算组成,而且这种算法采用塬位运算,故只需N个存储单元2. ∑∑(2)式(2)是FFT基4频域抽取算法的基本运算单元,一般称为蝶形运算。
1. 2点DFT运算称为蝶形运算,而整个FFT就是由若干级迭代的蝶形运算组成,而且这种算法采用塬位运算,故只需N个存储单元2. ∑∑(2)式(2)是FFT基4频域抽取算法的基本运算单元,一般称为蝶形运算。下一步再将X(4m+i),i=0,1,2,3分解成4个N42序列,迭代r次后完成计算,整个算法的复杂度减少为O(Nlog4N)
第一列蝶形运算只有一种类型:系数,参加运算的两个数据点间距为1。第二列有两种类型的蝶形运算:系数分别为 ,参加蝶形运算的两个数据点的间距等于2。第叁列有4种类型的蝶形运算:系数分别是 ,参加蝶形运算的两个数据点的间距等于4。可见,每一列的蝶形类型比前一列增加一倍,参加蝶形运算的两个数据点的间距也增大一倍,最后一列系数用得最多,为4个,即 ,而前一列只用到它偶序号的那一半,即,
第一列只有一个系数,即。上诉结论可以推广到N=的一般情况,规律是第一列只有一种类型的蝶形运算,系数是 ,以后每列的蝶形类型,比前一列增加一倍,到第是N/2个蝶形类型,系数是,共N/2个。由后向前每推进一列,则用上述系数中偶数序号的那一半,例如第列的系数则为参加蝶形运算的两个数据点的间距,则是最末一级最大,其值为N/2,向前每推进一列,间距减少一半。
FFT(快速傅里叶变换)作为数字信号处理领域的核心算法之一。蝶形运算单元是FFT设计的核心单元。本文研究基24FFT蝶形运算单元芯片设计。基于TSMC(***集成电路制造公司)0.18LmCMOS标准单元库的半定制ASIC(专用集成电路)设计,采用自顶向下、以关键模块为设计对象的设计方法,使用VerilogHDL描述系统,在Modelsim、DesignCompiler和ASTRO等EDA(电子设计自动化)工具中完成
基4FFT蝶形运算单元的设计
蝶形运算单元是FFT处理器的核心单元,蝶形运算单元结构的稳定性和运算的准确性直接影响到FFT处理器的性能。分析基4FFT的特点,综合考虑面积、性能、功耗各个方面的因素,设计出结合流水线技术和并行结构的蝶形运算单元。
蝶形运算单元结构设计
基24FFT中蝶形运算单元的处理结构见图
传统的基4算法是用3个复数乘法器和12个复数加法器构成,每次复数乘法器由4个实数乘法器和2个实数加法实现,每个复数加法由2个实数加法器实现。如此将基24算法的计算结构直接映射至硬件需消耗大量的逻辑资源(12个实数乘法器和22个实数加法器)。
经过重新排列如下:
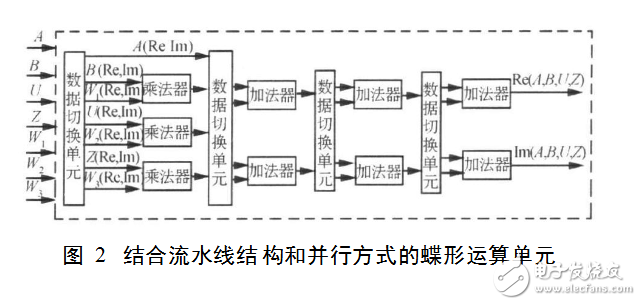
观察xc和uc,Xc和Uc,yc和zc,Yc和Zc这4组表达式,可以发现其对应的实部和虚部括号内的内容相同,因此可以将流水线方式与并行结构的思想巧妙结合起来,用4个循环序列对各寄存器进行严格的时序控制,只用1个实数乘法器来实现一次复数乘法器,对应3个不同的复数乘法用3个实数乘法并行进行;加法器也并行进行循环使用。因此,完成一个基4FFT蝶形运算单元仅需要3个实数乘法以及6个实数加法,相比传统基24FFT蝶形运算单元,可节省75%的乘法器逻辑资源和72.7%的加法器逻辑资源。
蝶形运算单元的结构如图2所示
数据切换单元
流水线技术与并行结构相结合的方法可以提高设计的灵活性,减小核心单元的面积,提高芯片运行的速度。流水线技术与并行结构相结合必须在时序的严格控制下执行。
数据切换单元由状态机组成,以蝶形运算单元的第1级数据切换单元为例。每组数据输入乘法器分为4个状态(分别为A、B、C、D)。状态A输入乘数的实部和旋转因子的实部;状态B输入乘数的实部和旋转因子的虚部;状态C输入乘数的虚部和旋转因子的实部;状态D输入乘数的虚部和旋转因子的虚部。其他3级数据切换单元根据前一级运算结构输出以此类推得到。每一级的具体结果以及步骤见表1。完成4级运算后,并行输出结果的实部和虚部
浮点乘法器的设计
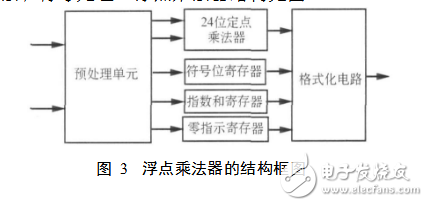
本设计中浮点数乘法器需完成2个IEEE754单精度浮点数之间的乘法,包括3个部分尾数乘法、指数加法和符号处理。浮点乘法器结构见图3
乘法的处理可分为3个步骤:
a)对输入数据进行预处理,即判断输入中是否有0,同时将输入数据的符号位、指数部分以及尾数部分拆开分别处理,符号位寄存,指数部分相加,尾数部分预处理;
b)将23位尾数和1位隐含位/10构成的24位有效数送入定点乘法器进行运算,并寄存预处理单元的其他输出数据;
c)接收定点乘法运算结果以及相关寄存器输出,将最终结果规格化为IEEE754标准单精度浮点格式。
24位定点乘法器采用了经典的阵列式结构结合改进Booth算法的树形结构。阵列式定点乘法器结构规整,适合于流水线处理,但是流水线深度过深,初始时延过长,硬件资源消耗过大。
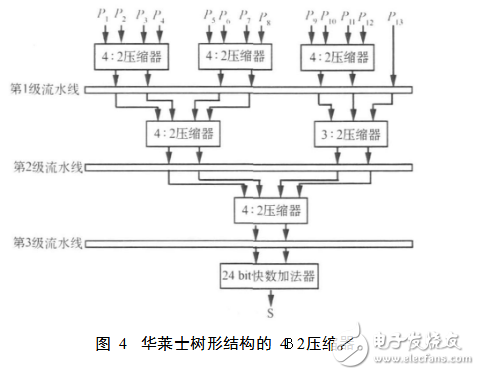
改进的Booth算法将24位定点乘法运算的部分积由24个压缩至13个,降低硬件开销,减少流水线级数。利用改进的Booth算法设计一种华莱士树形结构,如图4所示。
用3级4B2压缩器将13个部分积逐级压缩到2个,级间插入寄存器实现全流水,压缩后的2个部分积用快数加法器相加得到最终结果。4B2压缩器的逻辑结构见图5,由4B2压缩单元级联组成。
对并行的全加器进行逻辑化简可以得到4B2压缩单元,其逻辑表达式如下:
利用改进后的结构设计的定点乘法器流水线深度只有7级,降低了硬件成本,减小了流水线的初始延时,提高了系统的性能。
浮点乘法器的改进
分析4B2压缩器的逻辑表达式,可以发现当输入的a1,a2,a3,a4相同的时候,输出的Cout相同;当输入的a1,a2,a3,a4以及Cin相同时,输出的S和C都相同。
再分析Booth算法。Booth编码是针对有符号数的乘法,需要将符号位扩展并且移位;2个24bit定点数相乘,得到1个48bit的乘积,因此产生的部分积有2bit~24bit不等的相同符号位。
在华莱士树形结构中,Booth算法得到的13个48bit的部分积相加,只需要将其中的25bit相加,其他23bit可以通过分析直接得到和位和进位。每个乘法器节省了70个4B2压缩器,减少了关键路径时间,提高了乘法器的执行速度。
浮点加法器设计
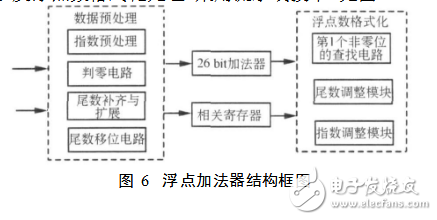
浮点加法器包括数据预处理电路、26bit加法器以及浮点数格式化处理,采用流水线技术,见图6。
浮点加法的处理步骤如下:
a)数据预处理部分,包括判零电路,如果其中一个加数为0,那么加法输出结果应该等于另一个加数;指数对齐;尾数移位实现尾数补齐和隐藏位/10扩展以及符号位扩展。
b)运用进位保留和进位传递相结合的26bit加法器。
c)将最终结果再格式化为IEEE754标准单精度浮点格式。
26bit定点加法器是浮点加法器的核心加法单元,本设计采用了超前进位和进位保留相结合的方法,见图7。超前进位加法器的特点是各级进位信号同时产生,大大减少了进位产生的时间,一般不超过4bi,t故将26bit分成6个3bit块和2个4bit块。其中,AF_3、AF_4采用超前进位加法器,26bit进位选择加法器仅用2级流水线就能达到所需性能要求。
浮点加法器的改进
在满足时序的情况下,分析26bit快速加法器。超前进位加法器适用于不超过4bit的数据,进位保留加法器是以面积换速度。如果采用两级流水线完成26bit加法器,时序上一定满足,但是却以24个AF_3和8个AF_4为代价。基于面积和时序的折衷优化,我们采用以下框图完成26bit加法器。只需要12个AF_3和4个AF_4即可完成26bit进位选择加法器。
逻辑综合
在蝶形运算单元结构完成之后,采用VerilogHDL对整个系统进行了RTL级描述和逻辑综合及功能验证。本文基于TSMC0.18LmCMOS标准单元库,使用Synopsys的DesignCompiler进行逻辑综合,使用Modsim进行仿真,并且与MATLAB计算结果进行对比。
逻辑综合
设计目标为200MHz时钟,设定20%裕量,因此约束时钟为4ns,具体约束条件如下:时钟周期4ns,时间抖动和歪斜0.1ns,线负载模型tsmc18_wl120,输入输出延时0.8ns,满足时序的情况下面积最小化。
综合完成后结果如图8所示。
蝶形运算单元逻辑综合报告显示关键路径延时3.4ns《4ns,所以slack为正。总单元面积1.12mm2,总的动态功耗为376.9mW。
基24FFT蝶形运算单元使用TSMC0.18LmCMOS标准单元库,能稳定工作在200MHz的时钟频率。采用改进的基24FFT蝶形结构图,将乘法器节省75%,加法器节省72.7%;采用改进的浮点乘法器和浮点加法器,使蝶形运算单元的面积节省了1.64万门。
此蝶形运算单元在满足200MHz的前提下,面积和功耗得到很大改善。对于N点FFT需要log4N级、每级N/4次蝶形运算,假设每级数据需要10点预存,数据输入输出需要1024@2个时钟,完成1024点运算的时间[(1024/4+10)@log41024+1024@2]@5ns=16.89ns。
可见,使用该蝶形运算单元构成FFT处理器在性能上处于领先地位。
 电子发烧友App
电子发烧友App











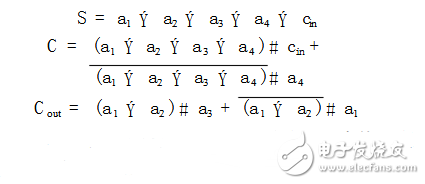








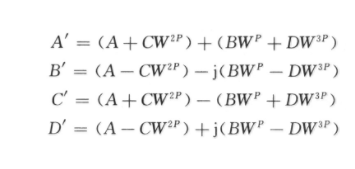










评论